Centru de masă
Centrul de masă sau centrul maselor este locația medie[necesită citare] a tuturor maselor sistemului. În cazul unui corp solid, poziția centrului maselor este determinată în raport cu acel corp. Folosirea centrului maselor permite adesea simplificarea ecuației de mișcare, fiind un punct de referință convenabil pentru calculul unor mărimi fizice, precum momentul cinetic sau momentul de inerție. În multe aplicații, ca cele din astrodinamică, corpurile pot fi înlocuite, în scopul analizării mișcării lor, prin masa lor aplicată în centrul maselor.
Termenul centrul maselor este adesea interschimbabil cu centrul de greutate, dar sunt concepte fizice diferite. Cele două centre se suprapun într-un câmp gravitațional uniform, de exemplu pentru corpurile aflate la suprafața Pământului, deoarece Pământul este mult mai mare în raport cu corpurile, iar forțele gravitaționale pot fi considerate paralele.
Într-un câmp gravitațional neuniform, centrul de greutate se referă la punctul în care se aplică rezultanta tuturor forțelor gravitaționale aplicate asupra corpului, iar cele două centre nu se mai suprapun. Diferența este mică dar măsurabilă în ceea ce privește, de exemplu, cuplul gravitațional care acționează asupra sateliților artificiali.
Baricentrul se referă de asemenea la centrul maselor.[necesită citare]
În general, centrul maselor unui corp nu corespunde cu centrul geometric al acestuia, iar acest lucru este exploatat de către inginerii proiectanți de mașini de sport, făcând ca centrul maselor să fie cât mai jos posibil pentru ca mașina să fie cât mai ușor manevrabilă. Un atlet care execută săritura în înălțime în stilul Fosbury Flop, își îndoaie corpul de așa natură încât este posibil să ștergă bara în timp ce centrul său de masă nu.[1]
Definiție
[modificare | modificare sursă]Centrul de masă al unui sistem de puncte materiale este punctul în raport cu care momentul static al sistemului este nul. Pentru a-l afla se ponderează raza vectoare cu masa ei , sumăm pentru toate masele sistemului și se divide cu masa întregului sistem. Se obține:
În cazul mediilor continue având densitatea și masa totală , suma se transformă în integrală:
Proiecțiile vectorului de poziție pe cele trei axe furnizează coordonatele carteziene ale centrului de masă:
Dacă un corp este omogen, el are aceeași densitate, iar centrul maselor corespunde cu centrul lui geometric.
Exemple
[modificare | modificare sursă]- Centrul de masă a două particule se află pe dreapta care leagă centrele lor de masă. Centrul de masă se află mai aproape de particula mai grea.
- Centrul de masă al unui inel cu densitate uniformă se află în centrul inelului, indiferent de materialul din care este alcătuit.
- Centrul de masă al unui triunghi solid omogen se află la intersecția medianelor triunghiului, care de altfel este și media celor trei vârfuri.
- Centru de masă al unui dreptunghi omogen se află la intersecția diagonalelor.
- Într-un corp cu simetrie sferică, centrul de masă se află în centrul geometric.[2] Acest lucru se aplică în mod aproximativ Pământului, deoarece densitatea variază considerabil, dar în adâncime și mai puțin în latitudine și longitudine.
- Mai general, dacă un corp are un plan de simetrie, centrul maselor se află în acel plan de simetrie. Dacă un corp are o axă de simetrie, centrul maselor se află pe axa de simetrie, iar dacă un corp are un centru de simetrie, centrul maselor se află în acel centru de simetrie.
Istoric
[modificare | modificare sursă]Conceptul centrului de masă a fost introdus pentru prima dată de fizicianul și matematicianul grec Arhimede. El a arătat că momentul exercitat pe o pârghie de mai multe greutăți aflate la diferite distanțe de-a lungul ei, este același cu momentul dat de toate greutățile mutate într-un singur punct, centrul lor de masă. În lucrarea Despre Corpurile Plutitoare el a demonstrat că orientarea corpului plutitor este de așa natură încât face ca centrul de masă să fie cât mai jos posibil. A dezvoltat tehnica matematică de găsire a centrului de masă al corpurilor cu densitate uniformă având diverse forme, în particular pentru triunghi, emisferă și pentru trunchiul unui paraboloid circular.
Legea a doua a lui Newton este refomulată în ceea ce privește centrul de masă din prima lege a lui Euler.
Proveniența centrului de masă
[modificare | modificare sursă]În următoarele ecuații de mișcare se presupune că există un sistem de particule guvernate de forțe interne și externe. Forțele interioare sunt cauzate de interacțiunea particulelor din interiorul sistemului, iar forțele exterioare sunt forțe care își au originea în afara sistemului, dar interacționează cu particulele din interiorul sistemului. Forțele exterioare nu apar neapărat datorită unui câmp uniform sau dintr-un potențial de forțe.
Pentru orice sistem în care nu există forțe externe, centrul de masă se mișcă cu viteză constantă. Acest lucru este valabil pentru toate sistemele cu forțe clasice interne, câmp electric, câmp magnetic, reacții chimice, etc. Mai precis, acest lucru este adevărat pentru orice forțe interne care satisfac legea a III-a a lui Newton (sisteme nedeformabile).
Impulsul total pentru orice sistem de particule este dat de:
în care M este masa totală, iar vcm este viteza centrului de masă. Viteza poate fi calculată luând derivata funcție de timp a poziției centrului de masă.
O forță analoagă legii a II-a a lui Newton este:
în care F este suma tuturor forțelor externe aplicate sistemului, iar acm este accelerația centrului de masă.
Fie forța internă a sistemului egală cu:
în care ete masa totală a sistemului, iar un vector care încă nu este definit. Deoarece iar atunci
Se obține deci o definiție vectorială a centrului de masă în funcție de forța totală din sistem. Această formă este folositoare pentru problema celor două corpuri.
Este logic să cerem ca, pentru orice sistem de mase, centrul de masă să se afle în interiorul înfășurătoarei convexe a sistemului. În particular, pentru două particule punctiforme, centrul de masă se află pe segmentul care leagă vârfurile vectorilor r1 și r2. Geometric, R - r1 = k(r2 - R) pentru o anumită valoare a constantei k. Luând distanțele în ambele părți ale ecuației, obținem d1 = kd2, în care d1 este distanța de la centrul de masă la corpului 1, iar d2 este distanța de la centrul de masă la corpului 2. Constanta k va depinde numai de masele m1 și m2 și vom examina natura acestei dependențe.
Presupunem că masa totală M este diferită de zero. Este clar că dacă m2 = 0, centrul de masă coincide cu cel al corpului 1, iar d1 = 0. Aceasta înseamnă că d2 = D, iar m1 = M. Simetria cere ca relația să rămână adevărată dacă schimbăm corpul 1 cu corpul 2.
Cel mai simplu model care satisface cerințele de mai sus este un model liniar, în care d1 = (D/M)m2 și d2 = (D/M)m1.
În acest model avem k = d1/d2 = m2/m1. După înmulțirea ecuației vectoriale cu m1, obținem m1(R - r1) = m2(r2 − R), sau (m1 + m2)R = m1r1 + m2r2. Astfel că,
Să presupunem acum că există și corpul al treilea de masă m3 și având vectorul de poziție r3. Pentru moment să rupem simetria celor trei corpuri și definim centrul de masă al celor trei corpuri ca centrul de masă a două corpuri determinat de corpul al treilea împreună cu un singur corp de masă M0 = m1 + m2 plasat în centrul de masă al corpurilor 1 și 2, al cărui vector de poziție este R0. Obținem:
Deoarece R se dovedește a fi simetric funcție de mi și ri, nu contează modul în care combinăn corpurile, în felul acesta putând extinde formula pentru n corpuri, obținând:
Deci modelul simplu al centrului de masă al celor două corpuri determină complet și unic formula pentru orice număr de mase. Scriind M = m1 + m2 + ... + mn, formula centrului de masă poate fi exprimată sub forma:
Diferențiind ambele părți ale ecuației obținem:
adică, suma impulsului unui număr oarecare de corpuri este egală cu impulsul centrului lor de masă. Acesta este principiul care dă expresia precisă a noțiunii intuitive că sistemul ca un tot se comportă ca masa totală M plasată în R, și justifică modelul simplu liniar unidimensional al centrului de masă.
Proprietăți ale centrului de masă
[modificare | modificare sursă]Centrul de masă este punctul geometric asociat sistemului în care se consideră concentrată toată masa acestuia, fiind deci util în descrierea mișcării globale a sistemului:
- Impulsul total al sistemului este egal cu masa sistemului înmulțită cu viteza centrului de masă:
- Rezultanta forțelor externe care acționează asupra sistemului este egală cu masa sistemului înmulțită cu accelerația centrului de masă:
- Momentul static al unui sistem de puncte materiale în raport cu un plan este egal cu produsul dintre masa sistemului și distanța centrului de masă la acel plan:
- Dacă sistemul de puncte materiale are un plan, o axă sau un centru de simetrie, centrul de masă se află în acel plan, pe acea axă sau în acel centru.
Demonstrație. Presupunând că sistemul admite planul ca plan de simetrie, oricărui punct de masă îi corespunde un punct de aceeași masă Cum rezultă deci centrul de masă se află în planul
Dacă se presupune că sistemul admite axa ca axă de simetrie, atunci unui punct de masă îi corespunde totdeauna un punct de aceeași masă Cum rezultă deci centrul de masă se află pe axa
Considerând că sistemul admite originea sistemului de referință ca centru de simtrie, din condițiile de simetrie rezultă că oricărui punct de masă îi corespunde întotdeauna un punct de aceeași masă Cum momentele statice rezultă deci centrul de masă se află în polul O.
- Dacă un sistem de puncte materiale se compune dintr-un număr de p subsisteme de mase și vectori de poziție ai centrelor de masă centrul de masă al sistemului se obține considerând masele sistemelor componente concentrate în centrele de masă
Demonstrație. Din relația se obține:
Deoarece:
relațiile (5.5) pot fi scrise:
Vectorul de poziție al centrului maselor sistemului este:
- Dacă un sistem de puncte materiale poate fi considerat ca provenind dintr-un sistem din care s-a extras un sistem și dacă se cunosc masele și centrele de masă definite de vectorii de poziție atunci centrul de masă al sistemului se poate obține considerând că masele și s-ar concentra în centrele de masă și
Demonstrație. Vectorul de poziție al centrului de masă C al sistemului are expresia:
Referitor la sistemele și se poate scrie conform (5.7) și (5.8):
Pentru întreg sistemul se obține:
Observație. Proprietățile centrului de masă prezentate pentru sisteme de puncte materiale sunt valabile și în cazul sistemelor de corpuri omogene.
Rotația și centrul de masă
[modificare | modificare sursă]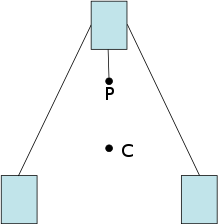

Centrul maselor numit adesea și centrul de greutate datorită câmpului gravitațional uniform g care acționează asupra sistemului ca și când masa M a sistemului se află concentrată în centru de masă R. Acest lucru este văzut cel puțin în două feluri:
- Energia potențială a unui sistem este egală cu energia potențială a unei particule care are aceeași masă M localizată în R.
- Momentul gravitațional al unui sistem egalează momentul unei forțe Mg care acționează în R:
Dacă câmpul gravitațional care acționează asupra unui corp nu este uniform, atunci centrul de masă nu are neapărat această proprietate convenabilă în ceea ce privește gravitația. Această situație a fost exprimată de Feynman în celebra sa carte The Feynman Lectures on Physics:[3]
„Centrul de masă este câteodată numit centrul de greutate, pentru motivul că, în multe cazuri, gravitația poate fi considerată uniformă. ...În cazul în care obiectul este așa de mare încât neparalelismul forțelor gravitaționale este semnificativ, atunci centrul în care trebuie aplicată forța de echilibru nu este simplu de descris, el depărtându-se ușor de centrul de masă. Iată de ce trebuie să facem distincție între centrul de masă și centrul de greutate.”
Chiar și atunci când se analizează forțele mareice de pe planetă, este suficient să folosim centrul de masă pentru a găsi mișcarea globală. În cazul câmpurilor neuniforme va trebui să vorbim de centrul de masă și nu de centrul de greutate.[4]
Inginerie
[modificare | modificare sursă]Semnificația în aeronautică
[modificare | modificare sursă]Centrul de masă este un punct important de pe avion, deoarece îi afectează în mod semnificativ stabilitatea, pentru că în timpul zborului centrul de masă variază în funcție de consumul de combustibil. Pentru a fi siguri că avionul este suficient de stabil și sigur pentru zbor, centrul de masă trebuie să varieze în anumite limite specificate, limite care sunt diferite de la avion la avion.
De regulă, pentru avioane cu aripi fixe, acestea sunt centrate în jurul unui punct aflat la un sfert din coarda aripii față de bordul ei de atac, numit focarul aripii. Dacă centrul de masă se află în fața acestui punct, avionul are o manevrabilitate scăzută și este posibil ca la decolare sau aterizare să nu se înalțe de bot. Dacă centrul de masă se află în spatele acestui punct, atunci el este ușor manevrabil, dar și instabil, iar dacă se află mult în spatele focarului să-l pună în imposibilitatea de a zbura.
Pentru elicoptere în planare, centrul de masă se află întotdeauna sub rotor. Pentru zborul de înaintare, centrul de masă se va muta spre spate pentru a echilibra momentul negativ de tangaj prin aplicarea controlului ciclic pentru propulsia elicopterului înainte; în consecință un elicopter de croazieră va zbura cu nasul în jos.
Baricentrul în astronomie și astrofizică
[modificare | modificare sursă]
Baricentrul (din greacă βαρύκεντρον) este punctul dintre două corpuri în care se echilibrează unul pe altul. De exemplu, este centrul de masă a două sau mai multe corpuri cerești în jurul căruia gravitează. Când un satelit natural gravitează în jurul unei planete, sau o planetă în jurul unei stele, ambele corpuri gravitează de fapt în jurul unui punct care se află între cele două centre de masă și mai aproape de corpul mai mare. De exemplu, Luna nu gravitează exact în jurul centrului Pământului, ci în jurul unui punct care leagă cele două centre de masă aflat la aproximativ 1710 km sub scoarța Pământului, punct în care cele două mase se echilibrează.
Baricentrul este unul din focarele orbitei eliptice a fiecărui corp. Acesta este un concept important în domeniul astronomiei, astrofizicii, ca și în problema celor două corpuri.
În problema celor două corpuri, r1 distanța de la centrul maselor la primul corp este dată de formula:
în care:
- a este distanța dintre cele două centre ale corpurilor, iar
- m1 și m2 sunt masele celor două corpuri.
r1 este în esență semi-axa mare a orbitei primului corp în jurul baricentrului — iar r2 = a − r1 este semi-axa mare a orbitei celui de al doilea corp. Dacă baricentrul se află localizat în interiorul celui mai masiv corp, mișcarea lui apare mai de grabă ca o oscilație decât ca o mișcare pe orbită.
În tabelul de mai jos sunt prezentate câteva exemple din sistemul solar. Valorile au fost rotunjite la trei cifre semnificative. În ultimele două coloane sunt date R1, raza corpului masiv și r1/R1, raportul dintre distanța la baricentru și rază. O valoare mai mică decât 1 arată că baricentrul se află în interiorul corpului masiv.
| Corpul masiv |
m1 (mE=1) |
Corpul mai mic |
m2 (mE=1) |
a (Km) |
r1 (km) |
R1 (km) |
r1/R1 |
|---|---|---|---|---|---|---|---|
| Observații | |||||||
| Pământul | 1 | Luna | 0.0123 | 384,000 | 4,670 | 6,380 | 0.732 |
| Pământul are o oscilație perceptibilă; vezi mareele. | |||||||
| Pluton | 0.0021 | Charon | 0.000254 (0.121 mPluton) |
19,600 | 2,110 | 1,150 | 1.83 |
| Ambele corpuri au orbite distincte în jurul baricentrului, dar Pluton și Charon erau considerate planete duble înainte de redefinirea cuvântului planetă din august 2006. | |||||||
| Soarele | 333,000 | Pământul | 1 | 150,000,000 (1 AU) |
449 | 696,000 | 0.000646 |
| Oscilația Soarelui este abia perceptibilă. | |||||||
| Soarele | 333,000 | Jupiter | 318 (0.000955 mSun) |
778,000,000 (5.20 AU) |
742,000 | 696,000 | 1.07 |
| Soarele gravitează baricentrul aproape de suprafața.[5] | |||||||
Dacă , ceea ce este adevărat pentru Soare în raport cu orice planetă, atunci putem aproxima raporul prin:
Atunci, baricentrul sistemului Soare-planetă va fi în afara Soarelui numai dacă:
Adică, atunci când planeta este masivă și departe de Soare.
Dacă planeta Jupiter ar avea orbita planetei Mercur (57,900,000 km, 0.387 AU), baricentrul sistemului Soare-Jupiter s-ar afla la 5,500 km de centrul Soarelui (r1/R1 ~ 0.08). Dacă Pământul ar avea orbita planetei pitice Eris (68 AU), baricentrul Soare-Pământ va fi tot în interiorul Soarelui la aproximativ 30,000 km de centru.
Pentru a calcula actuala traiectorie a Soarelui este necesară sumarea tuturor influențelor planetelor, cometelor, asteroizilor, etc, din sistemul solar. Dacă toate planetele ar fi aliniate de aceeași parte a Soarelui, centrul de masă combinat ar fi la aproximativ 500,000 km de suprafața soarelui. Acest calcul are la bază distanța medie dintre corpuri și valoarea medie r1. Dar toate orbitele corpurilor cerești sunt eliptice, iar distanțele dintre corpuri variază între apside în funcție de excentricitatea e. Atunci, poziția baricentrului variază ea, și este posibil ca pentru unele sisteme baricentrul să fie uneori în interiorul sau în exteriorul celui mai masiv corp. Această situație apare atunci când:
Animație
[modificare | modificare sursă]Imaginile sunt reprezentative.
 Două corpuri de mase egale gravitează în jurul baricentrului. (similar cu sistemul 90 Antiope) |
 Două corpuri cu mase diferite gravitează în jurul baricentrului precum sistemul Pluto–Charon. |
 Două corpuri cu diferență mare între mase gravitează în jurul baricentrului precum sistemul Pământ–Lună |
 Două corpuri cu diferență extremă între mase gravitează în jurul baricentrului precum sistemul Soare–Pământ |
 Două corpuri de mase similare gravitează în jurul baricentrului pe o orbită eliptică precum stelele binare | |||
Centrul de masă al unui corp omogen
[modificare | modificare sursă]În mecanică, corpul rigid se admite ca fiind un continuu material nedeformabil, adică orice element de volum are masă iar distanțele dintre puncte rămân nedeformate, indiferent de solicitările la care este supus corpul. Pentru a stabili o legătură cu rezultatele obținute în cazul sistemelor de n puncte materiale se consideră corpul divizat în volume elementare de mase
Când vectorul de poziție al centrului de masă:
unde este domeniul ocupat de corp și care se va nota cu în cazul blocurilor (corpuri cu trei dimensiuni), în cazul plăcilor (corpuri cu două dimensiuni, a treia fiind neglijabilă) și în cazul barelor (corpuri cu o singură dimensiune, celelalte fiind neglijabile în raport cu prima).
Corpul omogen este corpul a cărui densitate este aceeași în toate punctele sale. Cum densitatea sau masa specifică a corpului este definită prin raportul dintre masa coresounzătoare și volumul elementar,
vectorul de poziție al centrului de masă al blocului omogen este:
ale cărui coordonate sunt:
În cazul plăcilor se poate defini, în mod analog, densitatea superficială:
Vectorul de poziție al centrului de masă al plăcii omogene este:
ale cărui coordonate sunt:
În cazul barelor se definește densitatea liniară:
Vectorul de poziție al centrului de masă al barei omogene are expresia:
ale cărui coordonate sunt:
Locul centrului de masă
[modificare | modificare sursă]Al unei forme fizice arbitrare în 2D
[modificare | modificare sursă]Metoda este folositoare când se dorește găsirea centrului geometric al unei forme plane complexe de dimensiuni necunoscute și se bazează pe găsirea centrului de masă al corpului subțire cu densitate omogenă care are aceeași formă ca forma plană complexă.
Al unui obiect în formă de L
[modificare | modificare sursă]Aceasta este una din metodele de determinare a centrului de masă al obiectelor în formă de L.
- Se împarte forma în două dreptunghiuri (figura 2). Se caută centrul de masă al dreptunghiurilor prin trasarea diagonalelor. Se trasează dreapta care unește cele două centre de masă. Centrul de masă al formei L trebuie să fie pe linia AB.
- Se împarte forma în alte două dreptunghiuri (figura 3). Se caută centrul de masă al dreptunghiurilor prin trasarea diagonalelor. Se trasează dreapta care unește cele două centre de masă. Centrul de masă al formei L trebuie să fie pe linia CD.
- Centrul de masă al formei L se află la intersecția celor două drepre AB și CD, în punctul O. Punctul O poate să cadă sau nu în interiorul formei L.
Al unei forme compuse
[modificare | modificare sursă]Această metodă este folositoare când se dorește aflarea centrului geometric sau al centrului de masă al unui obiect care poate fi ușor împărțit în forme elementare ale căror centre de masă pot fi găsite ușor (vezi Lista centrelor geometrice). Întâi va fi găsit centrul de masă pe direcția x și apoi pe direcția y prin același procedeu.
 Forma este ușor de divizat într-un pătrat, triunghi și cerc. De notat că cercul va avea arie negativă.
Forma este ușor de divizat într-un pătrat, triunghi și cerc. De notat că cercul va avea arie negativă.
 Din Lista centrelor geometrice se notează coordonatele individuale ale centrului de masă al fiecărei figuri.
Din Lista centrelor geometrice se notează coordonatele individuale ale centrului de masă al fiecărei figuri.
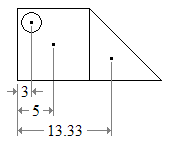 Se calculează centru de masă pe direcția x:
unități.
Se calculează centru de masă pe direcția x:
unități.

Centru de masă se află la distanța de 8.5 unități față de colțul din stânga-jos al figurii.
Prin urmărirea perimetrului în jurul unui obiect
[modificare | modificare sursă]Dezvoltarea planimetrului cunoscut și ca integraf, poate fi folosit la stabilirea centrului geometric sau al centrului de masă al unei forme neregulate. Această metodă poate fi aplicată formelor cu frontieră neregulată, netedă sau complexă, acolo unde alte metode ar fi prea dificile. Acest instrument a fost folosit de constructorii de nave pentru a se asigura că nava nu se răstoarnă.[6].
Centrul de greutate
[modificare | modificare sursă]Se consideră un sistem mecanic cu N componente de mase Poziția centrului de greutate este:
Dacă sistemul mecanic se află într-un câmp gravitațional uniform (accelerația gravitațională este constantă) atunci în formulele anterioare accelerația gravitațională g se simplifică, iar ecuațiile respective descriu poziția centrului de masă al sistemului.
Deci într-un câmp gravitațional uniform centrul de greutate coincide cu cel de masă.
Centrul forțelor paralele
[modificare | modificare sursă]Centrul forțelor paralele reprezintă punctul prin care trec axele centrale ale unui sistem de forțe paralele când acestea, fără să-și schimbe punctele de aplicație și nici mărimile lor scalare, se rotesc devenind paralele cu o altă axă. Dacă este vectorul de poziție al originei forței atunci vectorul de poziție al centrului forțelor paralele se definește prin:
Vezi și
[modificare | modificare sursă]- Centrul de greutate al unui avion
- Centrul de percuție
- Centrul de presiune
- Distribuția de greutăți
- Problema celor două corpuri
- Loc geometric
Note
[modificare | modificare sursă]- ^ Van Pelt, Michael (). Space Tourism: Adventures in Earth Orbit and Beyond. Springer. p. 185. ISBN 0387402136.
- ^ Giambattista, Alan; McCarthy Richardson, Betty; Coleman Richardson, Robert (), College physics, Volume 1 (ed. 2), McGraw-Hill Higher Education, p. 235, ISBN 0-071-10608-1
- ^ [1] The Feynman Lectures Set on Amazon
- ^ Symon, K. R. (1971). Mechanics, 3rd ed., Reading: Addison-Wesley
- ^ „What's a Barycenter?”. Space Place @ NASA. . Accesat în .
- ^ „Locating the center of mass by mechanical means” (PDF). Arhivat din original (PDF) la . Accesat în .
Note
[modificare | modificare sursă]- Voinea, Radu (). Introducere în mecanica solidului cu aplicații în inginerie. Editura Academiei Republicii Socialiste România.
- Feynman, Richard (). The Feynman Lectures on Physics. Addison Wesley. ISBN 0-201-02116-1.
- Goldstein, Herbert (). Classical Mechanics (ed. 3e). Addison Wesley. ISBN 0-201-65702-3.
- Kleppner, Daniel (). An Introduction to Mechanics (ed. 2e). McGraw-Hill. ISBN 0-07-035048-5.
- Marion, Jerry (). Classical Dynamics of Particles and Systems (ed. 4e). Harcourt. ISBN 0-03-097302-3.
- Murray, Carl (). Solar System Dynamics. Cambridge UP. ISBN 0-521-57295-9.
- Serway, Raymond A.; Jewett, John W. (). Physics for Scientists and Engineers (6th ed.). Brooks/Cole. ISBN 0-534-40842-7.
- Symon, Keithe R. (). Mechanics (ed. 3rd edition). Addison-Wesley. ISBN 0-201-07392-7.
- Tipler, Paul (). Physics for Scientists and Engineers: Mechanics, Oscillations and Waves, Thermodynamics (5th ed.). W. H. Freeman. ISBN 0-7167-0809-4.
Legături externe
[modificare | modificare sursă]- Center of Gravity Encyclopædia Britannica.
- Locating the center of mass by mechanical means Arhivat în , la Wayback Machine..
- The dynamic centre of gravity Engineer Xavier Borg - Blaze Labs Research
- Motion of the Center of Mass Arhivat în , la Wayback Machine. shows that the motion of the center of mass of an object in free fall is the same as the motion of a point object.
- The solar system's barycenter Simulations showing the effect each planet contributes to the solar system's barycenter
- Polygon Center of Mass Arhivat în , la Wayback Machine. An algorithm that would calculate the center of mass of a polygonal figure consisting of n points (x, y).



































































































































