Formula lui Euler
Formula lui Euler sau reprezentarea exponențială a unui număr complex spune că orice număr real x poate fi asociat unui număr complex de pe cercul unitate:
unde
- este baza logaritmului natural
- este unitatea imaginară
- și sunt funcțiile trigonometrice cu argumentul exprimat în radiani.
Richard Feynman a numit formula lui Euler "bijuteria noastră" și "cea mai remarcabilă formulă din matematică".[1]
Pentru cazul particular x = π este valabilă identitatea:
care combină într-o formulă simplă cele cinci numere fundamentale i, π, e,1 și 0.
Istoric
[modificare | modificare sursă]Roger Cotes în 1714 dădea un argument geometric intuitiv folosind cercul trigonometric și factorizarea complexă a unei sume de pătrate rezultată prin teorema lui Pitagora pentru formula lui Euler sub formă logaritmică:
(unde "ln" înseamnă logaritm natural, adică logaritm în bază e)[2][3].
Prima demonstrație a egalității în forma ei actuală datează din 1748, Euler bazându-și demonstrația pe egalitatea seriilor infinite din ambele părți ale egalității. Roger Cotes, prin argumentul său geometric, intuia oarecum reprezentarea geometrică a formulei bazată pe reprezentarea numerelor complexe ca puncte din planul complex, apărută ulterior abia după 50 de ani.
Euler considera firesc să prezinte studenților numerele complexe mult mai devreme decât se practică astăzi în predarea algebrei. În manualul său Elemente de Algebră el introduce aceste numere aproape de la început și le folosește de-a lungul întregii lucrări.
Aplicații în teoria numerelor complexe
[modificare | modificare sursă]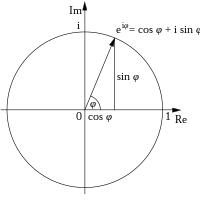
Formula lui Euler, numită astfel după Leonhard Euler, este o formulă matematică din analiza complexă care arată o relație strânsă între funcțiile trigonometrice și funcția exponențială complexă. (Identitatea lui Euler este un caz particular al formulei lui Euler.)
Această formulă poate fi interpretată spunând că funcția eix trasează cercul unitate din planul numerelor complexe când x ia valori reale. Aici, x este unghiul dintre o dreaptă care leagă originea cu un punct pe cercul unitate și axa reală pozitivă, măsurată în sens trigonometric în radiani. Formula este validă doar dacă sin și cos au argumentele exprimate în radiani, nu în grade.
Demonstrația originală se bazează pe dezvoltările în serie Taylor ale funcțiilor exponențială ez (cu z complex), sin x și cos x pentru numere reale x. De fapt, aceeași demonstrație arată că formula lui Euler este valabilă și pentru toate numerele complexe z.
Formula lui Euler poate fi folosită pentru a reprezenta numerele complexe în coordonate polare. Orice număr complex z = x + iy poate fi scris sub forma
unde
- partea reală
- partea imaginară
- modulul lui z
și este argumentul lui z— unghiul între axa x și vectorul z măsurat în sens trigonometric și în radiani — definit până la 2π.
Acum, luând această formulă derivată, se poate folosi formula lui Euler pentru a defini logaritmul unui număr complex. Pentru a face asta, se folosește și faptul că
și
ambele valabile pentru numerele complexe a și b.
De aceea se poate scrie:
pentru orice . Scoțând logaritm din ambele părți, rezultă:
și aceasta se poate folosi ca definiția logaritmului complex.
În fine, identitatea exponențială
care este valabilă pentru orice întreg k, împreună cu formula lui Euler implică anumite identități trigonometrice, precum și formula lui de Moivre.
Legăturile cu trigonometria
[modificare | modificare sursă]Formula lui Euler furnizează o legătură puternică între analiza matematică și trigonometrie, aducând o exprimare a funcțiilor sinus și cosinus ca sume ponderate ale funcției exponențiale:
Cele două ecuații de mai sus pot fi deduse adunând și scăzând formulele lui Euler:
și rezolvând pentru cosinus sau sinus.
Aceste formule pot servi chiar ca definiții ale funcțiilor trigonometrice de argument complex x. De exemplu, dacă x = iy sunt valabile egalitățile:
Exponențialele complexe pot simplifica trigonometria, deoarece sunt mai ușor de utilizat decât componentele lor sinusoidale. Una din tehnici este de a converti pur și simplu sinusoidele în expresii echivalente în termeni de exponențiale. După prelucrări, rezultatul simplificat are valori reale. De exemplu:
O altă tehnică este reprezentarea sinusoidelor în termeni de parte reală a unei expresii complexe, și de a face prelucrările pe acea expresie. De exemplu:
Alte aplicații
[modificare | modificare sursă]În ecuații diferențiale, funcția eix se folosește adesea pentru a simplifica derivările, chiar dacă rezultatul final este o funcție reală care implică sinus și cosinus. Identitatea lui Euler este o consecință imediată a formulei lui Euler.
În ingineria electrică dar și în alte domenii, semnalele ce pot varia periodic în timp sunt adesea descrise ca o combinație ponderată de sinus și cosinus, și acestea se exprimă mai convenabil ca partea reală a funcțiilor exponențiale cu exponent imaginar, folosind formula lui Euler. De asemenea, analiza fazorială a circuitelor poate include formula lui Euler pentru reprezentarea impedanței unui capacitor sau a unui inductor.
Demonstrații
[modificare | modificare sursă]Folosind seriile Taylor
[modificare | modificare sursă]Aceasta este o demonstrație a formulei lui Euler folosind dezvoltări în serie Taylor și proprietățile puterilor lui i:
și așa mai departe. Funcțiile ex, cos(x) și sin(x) (presupunând că x este număr real) pot fi exprimate folosind dezvoltările lor în serie Taylor în jurul lui zero:
Pentru z complex se definește fiecare funcție prin seriile de mai sus, înlocuind x cu z. Aceasta este posibil, deoarece raza de convergență a fiecărei serii este infinită. Atunci rezultă că
Rearanjarea termenilor se justifică deoarece fiecare serie este absolut convergentă. Luând z = x număr real rezultă identitatea originală așa cum a descoperit-o Euler.
Folosind derivata
[modificare | modificare sursă]Pornind de la o reprezentare geometrică a funcțiilor trigonometrice se poate ajunge la formula exponențială complexă.
Se definește o funcție prin următoarea expresie algebrică:
unde cosinusul și sinusul sunt notate f1(x) și f2(x), urmând a exprima și derivatele acestor funcții prin aceleași notații datorită valorilor acestor derivate.
Aceasta este permisă deoarece ecuația
implică faptul că nu este niciodată zero.
Derivata funcției , conform regulii câtului și tratând unitatea imaginară i ca pe o constantă oarecare, este nulă:
Deci, având derivata nulă trebuie să fie o funcție constantă. Astfel,
Rearanjând, rezultă că
Folosind egalități între derivate și funcții
[modificare | modificare sursă]Tot de la reprezentarea geometrică a funcțiilor trigonometrice se poate ajunge la formula exponențială complexă.
Se consideră funcția g(x) prin
i fiind constantă, primele două derivate ale lui g(x) sunt
deoarece i 2 = −1 prin definiție. De aici se poate scrie următoarea egalitate între derivata de ordinul doi și funcția inițială cu semn schimbat, adică o ecuație diferențială ordinară liniară de ordinul 2:
sau
Pentru această egalitate se constată existența a două funcții reale pentru care este valabilă egalitatea: atât cos(x) cât și sin(x) sunt funcții reale a căror a doua derivată este identică cu funcția inițială cu semnul minus.
Aceste două funcții sunt soluțiile acestei ecuații diferențiale liniare de ordinul doi. Ecuația admite și orice sumă a acestor două funcții înmulțite cu constante numerice oarecare (combinație liniară de soluții particulare ale unei ecuații diferențiale omogene) tot ca o soluție. Atunci, în general, soluția ecuației diferențiale este
pentru orice constante A și B. Dar nu toate valorile acestor două constante satisfac condițiile particularizatoare pentru funcția g(x) specificată mai sus:
- .
Condițiile inițiale (aplicate soluției generale) sunt
și permit obținerea valorilor pentru A și B
și în final egalitatea de demonstrat:
Note
[modificare | modificare sursă]- ^ Feynman, Richard P. (). The Feynman Lectures on Physics, vol. I. Addison-Wesley. pp. p. 22–10. ISBN 0-201-02010-6.
- ^ Cotes scria: "Nam si quadrantis circuli quilibet arcus, radio CE descriptus, sinun habeat CX sinumque complementi ad quadrantem XE ; sumendo radium CE pro Modulo, arcus erit rationis inter & CE mensura ducta in ." (Astfel dacă vreun arc al unui cadran de cerc, descris de raza CE, are sinusul CX și sinusul complementului raportat la cadran XE ; luând raza CE ca modul, arcul va fi măsura raportului dintre & CE multiplicat cu .)
Considerând un cerc cu centrul E (în originea planului (x,y)) și raza CE și un unghi θ cu vârful în E având axa x pozitivă ca una din laturi și o rază CE ca cealaltă latură. Perpendiculara din punctul C de pe cerc la axa x e "sinusul" CX ; linia dintre centrul cercului E și punctul X de pe piciorul perpendicularei e XE, care e "sinus complementului raportat la cadran" sau "cosinus". Raportul dintre și CE e astfel . In terminologia lui Cotes, "măsura" unei mărimi e logaritmul său natural, iar "modulul" un factor de conversie care transformă măsura unui unghi în lungimea unui arc al unui cerc (aici modululul e raza (CE) cercului). Conform lui Cotes, produsul modulului și al măsurii (logaritm) raportului, la multiplicarea cu , egalează lungimea arcului subintins de θ, care pentru orice unghi măsurat în radiani e CE • θ. Astfel, . Această egalitate are semn greșit: factorul ar trebui să fie în partea dreaptă a egalității, nu în stânga. Făcând această schimbare, după împărțirea ambilor membrii cu CE și exponentiere în ambii membrii, rezultatul e: , care e formula lui Euler.
A se vedea:- Roger Cotes (1714) "Logometria," Philosophical Transactions of the Royal Society of London, 29 (338) : 5-45 ; în special pagina 32. Disponibilă on-line la: Hathi Trust
- Roger Cotes with Robert Smith, ed., Harmonia mensurarum … (Cambridge, England: 1722), capitol: "Logometria", p. 28.
- ^ John Stillwell (). Mathematics and Its History. Springer.





























































