Deplasare spre roșu

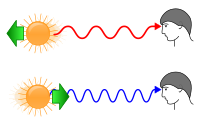
În fizică și astronomie, deplasarea spre roșu are loc când lungimea de undă a radiației electromagnetice - de regulă lumina vizibilă - emise sau reflectate de un obiect este deplasată spre domeniul de energie mică (roșu) al spectrului electromagnetic din cauza efectului Doppler sau a altor efecte gravitaționale. În general, deplasarea spre roșu se definește ca fiind o creștere a lungimii de undă a radiației electromagnetice receptată de un detector în comparație cu lungimea de undă emisă de sursă. Această creștere a lungimii de undă corespunde unei scăderi a frecvenței radiației electromagnetice.
Orice creștere a lungimii de undă se numește „deplasare spre roșu”, chiar dacă are loc în spectrul invizibil al radiațiilor electromagnetice, cum ar fi radiații gamma, radiații X și ultraviolete. Această denumire poate fi derutantă deoarece, pentru lungimi de undă mai mari decât ale luminii roșii (de exemplu, infraroșii, microunde și unde radio), deplasarea spre roșu duce radiația în direcția opusă față de lumina roșie.
O deplasare spre roșu observată și datorată efectului Doppler are loc atunci când sursa de lumină se îndepărtează de observator, analog deplasării Doppler care modifică frecvența percepută a undelor sonore emise de sursele ce se îndepărtează de observator. Deși observarea acestor deplasări spre roșu are multe aplicații terestre (de exemplu, radarul Doppler și radarele auto),[1] deplasările Doppler spre roșu sunt utilizate în special în astrofizica spectroscopică pentru a determina mișcarea relativă față de Pământ a obiectelor astronomice îndepărtate.[2]
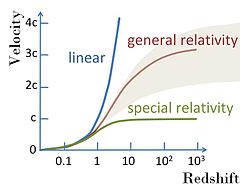
O formulă a deplasării spre roșu relativistă (și aproximarea sa newtoniană) se utilizează atunci când spațiul-timp este izotrop. Atunci când devin importante efectele gravitaționale, deplasarea spre roșu trebuie calculată folosind teoria relativității generale[3]. Două formule importante pentru cazuri speciale sunt așa-numita formulă a deplasării spre roșu gravitaționale, care se aplică oricărui câmp gravitațional staționar (adică invariant în timp), și formula deplasării spre roșu cosmologice care se aplică universului în expansiune din cosmologia Big Bang.[4]
Deplasările spre roșu relativiste, gravitaționale și cosmologice pot fi înțelese din perspectiva legilor transformării sistemelor de referință. Există și alte procese fizice ce pot conduce la modificarea frecvenței radiației electromagnetice și care nu sunt în general denumite „deplasări spre roșu”, printre care împrăștierea radiațiilor și efectele optice cum sunt refracția și aberația cromatică.
Istorie[modificare | modificare sursă]
Istoria subiectului a început cu dezvoltarea în secolul al XIX-lea a mecanicii undelor și cu explorarea diverselor fenomene asociate cu efectul Doppler. Acest efect poartă numele lui Christian Andreas Doppler, care a oferit prima explicație fizică cunoscută a fenomenului în 1842.[5] Ipoteza a fost verificată și confirmată pentru undele sonore de către omul de știință olandez Christoph Hendrik Diederik Buys Ballot în 1845.[6] Doppler a prezis corect că fenomenul trebuie să se aplice tuturor undelor, și în particular a sugerat că variația culorilor stelelor ar putea fi atribuită mișcării lor în raport cu Pământul.[7] Deși această presupunere s-a dovedit incorectă (culorile stelelor sunt dependente de temperatura de la suprafața acestora, și nu de mișcarea lor), s-a dovedit ulterior că există și un astfel de efect.
Prima deplasare spre roșu Doppler a fost descrisă în 1848 de fizicianul francez Armand-Hippolyte-Louis Fizeau, care a arătat că deplasarea liniilor spectrale observabilă la stele se datorează efectului Doppler. În 1868, astronomul britanic William Huggins a fost primul care a calculat prin această metodă viteza cu care o stea se îndepărtează de Pământ.[8]
În 1871, a fost confirmată deplasarea optică spre roșu când fenomenul a fost observat la liniile Fraunhofer pentru rotația solară, constatându-se deplasarea spre roșu ale acestora cu aproximativ 0,1 Å.[9] În 1901 Aristarh Belopolski a verificat deplasarea optică spre roșu în laborator cu ajutorul unui sistem de oglinzi rotative.[10]
Prima apariție a termenului „deplasare spre roșu” a fost în 1908, când astronomul american Walter S. Adams menționa „Două metode de cercetare a acelei naturi a deplasării spre roșu nebulare”.[11]
Începând cu observațiile din 1912, Vesto Slipher a descoperit că majoritatea nebuloaselor spirale prezentau deplasări spre roșu considerabile.[12] Ulterior, Edwin Hubble a descoperit o relație aproximativă între deplasarea spre roșu a unor astfel de „nebuloase” (despre care nu se știa încă faptul că sunt de fapt galaxii) și distanța până la ele cu formularea legii care îi poartă numele.[13] Aceste observații, coroborate cu lucrările lui Alexander Friedman din 1922 în care a calculat celebrele sale ecuații,[14] sunt astăzi considerate dovezi puternice ale expansiunii universului și ale teoriei Big Bang.[15]
Măsurare și interpretare[modificare | modificare sursă]
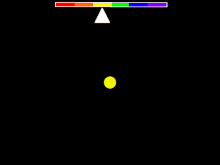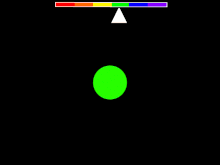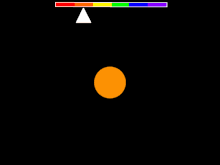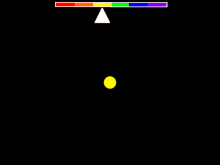
Spectrul luminii care provine dintr-o singură sursă se poate măsura. Pentru a determina deplasarea spre roșu, se identifică în spectru caracteristici cum ar fi liniile spectrale, linii de emisie, sau de absorbție sau alte variații remarcabile ale intensității luminii. Dacă acestea sunt găsite, ele se pot compara cu caracteristicile similare din spectrul de emisie sau absorbție ai diferiților compuși chimici detectabili și măsurabili în experimente de laborator. Un element atomic foarte frecvent întâlnit în spațiu este hidrogenul. Spectrul luminii inițial lipsită de caracteristici și trecută prin hidrogen prezintă un spectru specific acestui element cu caracteristici la intervale regulate. Dacă observația se limitează la liniile de absorbție, rezultatul ar fi similar cu ilustrația din dreapta-sus. Dacă se observă aceeași structură de intervale dintre liniile spectrale dar cu un decalaj constant al lungimilor de undă într-un spectru observat la o sursă îndepărtată, atunci acel spectru se poate identifica tot cu al hidrogenului. Dacă se identifică aceeași linie spectrală în ambele spectre dar la lungimi de undă diferite, atunci se poate calcula deplasarea spre roșu cu formulele din tabelul de mai jos. Determinarea deplasării spre roșu a unui obiect în acest fel necesită o gamă de frecvențe sau de lungimi de undă. Pentru a calcula deplasarea spre roșu pentru un spectru fără caracteristici identificabili, trebuie să se cunoască lungimea de undă a luminii emise în sistemul de referință în care sursa este în repaus, cu alte cuvinte, lungimea de undă ce ar fi măsurată de un observator aflat în mișcare solidar cu sursa (într-un sistem de referință propriu). Cum în aplicațiile astronomice, această măsurătoare nu se poate efectua direct, se folosește în schimb metoda cu linii spectrale descrisă aici. Deplasările spre roșu nu se pot calcula pentru caracteristicile neidentificate ale căror frecvență în sistemul de referință propriu nu se cunoaște, sau cu un spectru lipsit de caracteristici sau cu zgomot alb (fluctuații aleatoare într-un spectru).[16]
Deplasarea spre roșu (și cea spre albastru) pot fi caracterizate prin diferența relativă dintre lungimile de undă (sau frecvențele) emise și cele observate ale unui obiect. În astronomie, se obișnuiește ca această cantitate adimensională să fie denumită z. Dacă λ reprezintă lungimea de undă, și f reprezintă frecvența (atenție, λf = c unde c este viteza luminii), atunci z se definește prin ecuațiile:
| Pe baza lungimii de undă | Pe baza frecvenței |
|---|---|
După ce se măsoară z, distincția dintre deplasarea spre roșu și cea spre albastru este doar o chestiune de semn al lui z. De exemplu, deplasarea spre albastru cauzată de efectul Doppler (z < 0) se asociază cu obiecte ce se apropie de observator și cu deplasarea spectrului luminii spre energii mai mari. Analog, deplasarea spre roșu cauzată de efectul Doppler (z > 0) se asociază cu obiecte ce se îndepărtează de observator și cu deplasarea spectrului luminii spre energii mai mici. Tot astfel, deplasările spre albastru gravitaționale se asociază cu lumina emisă dintr-o sursă aflată într-un câmp gravitațional mai slab observat în cadrul unui câmp gravitațional mai puternic, iar deplasarea spre roșu gravitațională implică circumstanțe inverse.
Formulele deplasării spre roșu[modificare | modificare sursă]
În teoria relativității generale, se pot calcula formule pentru cazuri particulare importante ale deplasării spre roșu în anumite geometrii particulare ale spațiu-timpului, așa cum rezumă următorul tabel. În toate cazurile, modulul deplasării (z) este independent de lungimea de undă.[2]
| Tip de deplasare spre roșu | Geometrie | Formulă[17][18] |
|---|---|---|
| Doppler relativist | Spațiu Minkowski (spațiu-timp izotrop) | ( pentru mic) |
| Deplasarea cosmologică spre roșu | spațiu-timp FLRW (univers Big Bang în extindere) | |
| Deplasarea gravitațională spre roșu | orice spațiu-timp staționar (de ex. geometria Schwarzschild) | (pentru geometria Schwarzschild, ) |
Efectul Doppler[modificare | modificare sursă]
Dacă o sursă de lumină se îndepărtează de observator, atunci are loc deplasarea spre roșu (z > 0); dacă sursa se apropie de observator, atunci are loc deplasarea spre albastru (z < 0). Aceasta este valabilă pentru toate undele electromagnetice și este explicată de efectul Doppler. Ca o consecință, acest tip de deplasare spre roșu se numește deplasare Doppler spre roșu. Dacă sursa se îndepărtează de observator cu viteza v, atunci, ignorând efectele relativiste, deplasarea spre roșu este dată de formula
- (Cum )
unde c este viteza luminii. În cazul efectului Doppler clasic, frecvența sursei nu se modifică, iar mișcarea recesională cauzează iluzia de frecvență mai mică.
Efectul Doppler relativist[modificare | modificare sursă]
O tratare mai completă a deplasării Doppler spre roșu impune luarea în calcul a efectelor relativiste asociate cu mișcarea surselor cu viteze apropiate de viteza luminii. Pe scurt, deplasarea spre roșu a luminii emise de obiectele ce se apropie de viteza luminii va suferi deviații de la formula de mai sus din cauza dilatării spațiu-timpului din teoria relativității restrânse, deviații care pot fi corectate prin introducerea factorului Lorentz γ în formula efectului Doppler clasic după cum urmează:
unde, factorul Lorentz se exprimă prin relația:
în care c reprezintă viteza luminii, și v este viteza relativă a sursei față de observator.
Acest fenomen a fost observat pentru prima oară într-un experiment efectuat în 1938 de Herbert E. Ives și de G.R. Stilwell și numit experimentul Ives-Stilwell.[19]
Cum factorul Lorentz depinde doar de modulul vitezei, acesta determină ca deplasarea spre roșu asociată corecției relativiste să fie independentă de orientarea mișcării sursei. Spre deosebire de aceasta, partea clasică a formulei depinde de proiecția vitezei sursei pe direcția de observare, ceea ce dă rezultate diferite pentru orientări diferite. În consecință, pentru un obiect ce se mișcă sub un unghi θ față de direcția sursă-observator (unghiul zero corespunde situației în care vectorul viteză al sursei este coliniară cu direcția de observare), forma completă a efectului Doppler relativist devine:
și pentru mișcarea ce are loc doar de-a lungul direcției de observare (θ = 0°), ecuația se reduce la:
Pentru cazul special al sursei în mișcare pe o direcție normală (θ = 90°) față de detector, deplasarea relativistă este cunoscută sub numele de deplasarea spre roșu transversală, și determină o deplasare dată de expresia:
deși obiectul nu se îndepărtează instantaneu de observator. Chiar dacă sursa se îndreaptă spre observator, dacă există o componentă transversală a mișcării, atunci există o viteză limită la care dilatarea temporală anulează deplasarea spre albastru și pentru viteze mai mari decât această viteză limită de apropiere a sursei, lumina acesteia va fi deplasată spre roșu în loc de albastru.[20]
Expansiunea spațiului[modificare | modificare sursă]
În prima parte a secolului al XX-lea, Slipher, Hubble și alții au efectuat primele măsurători ale deplasărilor spre roșu și albastru ale galaxiilor de dincolo de Calea Lactee. Inițial, ei au interpretat aceste deplasări ca fiind datorate doar efectului Doppler, dar ulterior Hubble a descoperit o oarecare corelație între creșterea deplasării spre roșu și distanța față de galaxii. Teoreticienii au realizat aproape imediat că aceste observații pot fi explicate și printr-un alt mecanism de producere a deplasării spre roșu. Legea lui Hubble a corelației între deplasarea spre roșu și distanță stă la baza modelelor cosmologice bazate pe relativitatea generală și care prezintă o expansiune metrică a spațiului.[15] Ca rezultat, fotonii propagați prin spațiul în extindere sunt „întinși”, creând o deplasare cosmologică spre roșu. Aceasta diferă de deplasarea dată de efectul Doppler și descrisă mai sus prin aceea că diferența de viteză (respectiv transformarea Lorentz) dintre sursă și observator nu se datorează schimbului clasic de impuls și energie, și că fotonii își măresc lungimea de undă și deci se deplasează spre roșu din cauză că spațiul prin care se propagă ei se dilată (extinde).[22] Consecințele observabile ale acestui efect pot fi calculate folosind ecuațiile din teoria relativității generale care descriu un univers omogen și izotrop[23].
Pentru calculul efectului de deplasare spre roșu, se folosește ecuația geodezicii pentru o undă de lumină plană, adică
unde
- este elementul linie (Lorentzianul)
- este intervalul de timp (infinitezimal)
- este intervalul spațial (infinitezimal)
- este viteza luminii
- este factorul cosmic de scală, dependent de timp sau factorul de scalare Robertson-Walker
- este curbura locală pe unitatea de arie.
Pentru un observator ce privește frontul unei unde luminoase la o poziție și la un moment de timp , acel front de undă a fost emis la un moment în trecut și la o poziție aflată la o distanță . Integrând pe drumul parcurs de undă în spațiu și în timp se obține:
În general, lungimea de undă a luminii nu este aceeași pentru cele două poziții și momente considerate din cauza variației proprietăților metricii. Când unda a fost emisă, ea avea o lungime de undă de . Următorul maxim al undei luminoase a fost emis la un moment
Observatorul vede următorul maxim al undei luminoase observate cu o lungime de undă care sosește la un moment de timp
Deoarece al doilea maxim este din nou emis de la și este observat la , se poate scrie următoarea ecuație:
Părțile din dreapta celor două ecuații integrale de mai sus sunt identice, ceea ce înseamnă că
sau, analog,
Pentru variații foarte mici ale timpului (în intervalul unei perioade de oscilații a undei) factorul de scală este în esență o constantă ( la momentul prezent și pentru momentul din trecut). De aici
ceea ce se poate scrie sub forma:
Folosind definiția deplasării spre roșu dată mai sus, se obține ecuația

Într-un univers în expansiune, cum este cel în care existăm, factorul de scalare este monoton crescător în timp, și deci, z este pozitiv, iar galaxiile îndepărtate apar deplasate spre roșu. Acest tip de deplasare spre roșu se numește deplasare cosmologică spre roșu sau deplasare Hubble. Dacă universul s-ar fi contractat în loc să se extindă, am vedea galaxiile îndepărtate deplasate spre albastru cu o cantitate proporțională cu distanța până la ele.[27]
Aceste galaxii nu se îndepărtează doar ca viteză fizică; mai mult, spațiul dintre ele se lărgește, ceea ce explică izotropia pe scară mare a efectului, cerută de principiul cosmologic.[28] Pentru deplasări cosmologice spre roșu de z < 0,01 efectele expansiunii spațiu-timpului sunt minime și deplasările cosmologice spre roșu pot fi dominate de alte deplasări Doppler și deplasări spre albastru adiționale cauzate de mișcările relative stranii ale galaxiilor.[29] Diferența dintre viteza fizică și expansiunea spațiului se poate ilustra cu ajutorul universului modelat de o folie cauciuc, o analogie cosmologică adesea utilizată pentru a descrie expansiunea spațiului. Dacă două obiecte sunt reprezentate de niște bile metalice și spațiu-timpul de o suprafață de cauciuc, efectul Doppler este cauzat de mișcarea bilelor pe suprafață pentru a crea mișcare stranie. Deplasarea cosmologică spre roșu are loc atunci când bilele se sprijină pe suprafață și aceasta este întinsă. (Evident, modelul prezintă probleme dimensionale, deoarece bilele trebuie să fie în suprafața de cauciuc, iar deplasarea cosmologică produce viteze mai mari decât produce efectul Doppler dacă distanța între două obiecte este suficient de mare.)
Utilizând un model al expansiunii universului, deplasarea spre roșu poate fi legată de vârsta unui obiect observat, așa-numita relație timp cosmic–deplasare spre roșu. Se notează raportul de densitate ca Ω0:
unde ρcrit este densitatea critică a materiei pentru care universul trece de la starea de expansiune la aceea de contracție (colaps). Această densitate este aproximativ de trei atomi de hidrogen pe mia de litri de spațiu.[30] La deplasări spre roșu mari, rezultă:
unde H0 = astăzi constanta Hubble, și z = deplasarea spre roșu.[31][32][33]
Deplasarea spre roșu a galaxiilor include atât o componentă legată de viteza de îndepărtare provenită din expansiunea universului, cât și o componentă legată de deplasarea Doppler. Deplasarea spre roșu cauzată de expansiunea universului depinde de viteza de îndepărtare într-o manieră determinată de modelul cosmologic ales pentru a descrie expansiunea universului, ceea ce diferă foarte mult de felul în care deplasarea Doppler depinde de viteza locală.[34] Descriind originea deplasării spre roșu în expansiunea cosmologică, Harrison spune: „Lumina pleacă de la o galaxie aflată în repaus în regiunea sa de spațiu, și este în cele din urmă primită de observatori în repaus în regiunea lor locală de spațiu. Între galaxie și observator, lumina se deplasează prin regiuni vaste de spațiu aflat în expansiune. Ca rezultat, toate lungimile de undă ale luminii sunt „întinse” de expansiunea spațiului. Pur și simplu.” Vezi Harrison, p. 315.[22] „Creșterea de lungime de undă de la emisia la absorbția luminii nu depinde de viteza de modificare a lui a(t) (aici a(t) este factorul de scalare Robertson-Walker) la momentele emisiei și recepției, ci de creșterea lui a(t) de-a lungul întregului interval de timp scurs de la emisie și până la recepție.”[35]
Cu toate acestea, literatura populară utilizează adesea expresia „deplasare Doppler spre roșu” în loc de „deplasare cosmologică spre roșu” pentru a descrie deplasarea spre roșu a galaxiilor cauzată de expansiunea spațiu-timpului, în pofida faptului că deplasarea spre roșu nu se calculează folosind ecuația Doppler relativistă.[36] În particular, deplasarea Doppler spre roșu este limitată de teoria relativității restrânse; astfel, aici v > c este imposibil în timp ce v > c este posibil în cazul deplasării cosmologice spre roșu deoarece spațiul care separă obiectele (de exemplu, un quasar de Pământ) se pot extinde mai rapid decât viteza luminii.[37] Dintr-un punct de vedere mai matematic, ideea că „galaxiile îndepărtate se îndepărtează și mai mult” și cea că „spațiul dintre galaxii se extinde” sunt legate de schimbarea sistemelor de coordonate. Exprimarea precisă a acestora impune lucrul cu matematica metricii Friedmann-Robertson-Walker.[38]
Deplasare spre roșu gravitațională[modificare | modificare sursă]
În teoria relativității generale, există o dilatare temporală într-o groapă gravitațională. Aceasta este cunoscută ca Deplasare spre roșu gravitațională sau deplasare Einstein.[39][40] Calculul teoretic al acestui efect rezultă din soluția Schwarzschild a ecuațiilor lui Einstein care dau următoarea formulă a deplasării spre roșu asociate cu deplasarea unui foton în câmpul gravitațional al unei mase sferic simetrice neîncărcată electric, fără mișcare de rotație:
unde
- este Constanta gravitațională,
- este masa obiectului care creează câmpul gravitațional,
- este coordonata radială a observatorului (analog distanței clasice din centrul obiectului, dar de fapt coodonată Schwarzschild), și
- este viteza luminii.
Acest rezultat al deplasării spre roșu gravitaționale poate fi calculat din ipotezele relativității restrânse și din principiul de echivalență; utilizarea ansamblului teoriei relativității generale nu este necesară.[41]
Efectul este foarte mic, dar măsurabil pe Pământ folosind efectul Mössbauer și a fost observat pentru prima oară în experimentul Pound-Rebka.[42] Acest efect este însă semnificativ doar în apropierea unei găuri negre, și pe măsură ce un obiect se apropie de orizontul evenimentelor deplasarea spre roșu devine infinită. El este și cauza dominantă a fluctuațiilor de temperatură pe scară unghiulară mare în radiația cosmică de fundal (efectul Sachs-Wolfe).[43]
Observații în astronomie[modificare | modificare sursă]
Deplasarea spre roșu observată în astronomie se poate măsura fiindcă spectrele de emisie și de absorbție ale diverselor specii atomice sunt caracteristici distinctive și bine cunoscute, calibrate prin experimentele spectroscopice efectuate în laboratoarele de pe Pământ. Când se măsoară deplasarea spre roșu a diverselor linii de emisie și absorbție ale unui singur obiect astronomic, z rezultă a fi remarcabil de constant. Deși obiectele îndepărtate pot fi ușor neclare și cu liniile lărgite, aceasta se poate explica doar prin mișcarea termică sau mecanică a sursei. Din aceste motive, consensul între astronomi este că deplasările spre roșu pe care le observă se datorează unei combinații de trei forme stabilite de deplasare spre roșu. Ipotezele și explicațiile alternative ale deplasării spre roșu, cum ar fi lumina obosită nu sunt în general considerate plauzibile.[44]
Spectroscopia, ca metodă de măsurare, este considerabil mai dificilă decât simpla fotometrie, care măsoară strălucirea obiectelor astronomice prin anumite filtre.[45] Când sunt disponibile doar date fotometrice (de exemplu, Hubble Deep Field și Hubble Ultra Deep Field), astronomii se bazează pe o tehnică de măsurare a deplasării fotometrice spre roșu.[46] Deoarece filtrul este sensibil la o gamă de lungimi de undă și deoarece tehnica se bazează pe multe presupuneri asupra naturii spectrului sursei de lumină, erorile pentru acest gen de măsurători pot fi de până la δz = 0,5, și ele sunt mult mai nesigure decât cele spectroscopice.[47] Fotometria, însă, permite cel puțin o caracterizare calitativă a deplasării spre roșu. De exemplu, dacă un spectru similar cu cel solar ar avea o deplasare spre roșu de z = 1, el ar fi cel mai strălucitor în infraroșu decât în zona galben-verde de culoare a spectrului vizibil asociată cu maximul spectrului său de corp negru, și intensitatea luminii va fi redusă în filtru cu un factor de doi (1+z).[48]
Observații locale[modificare | modificare sursă]
La obiectele apropiate (din galaxia Calea Lactee) deplasările spre roșu observate sunt aproape întotdeauna în legătură cu vitezele fizice de-a lungul direcției de observare. Observarea acestor deplasări spre roșu și spre albastru au permis astronomilor sa măsoare vitezele și să parametrizeze masele stelelor ce orbitează împreună cu alte stele în sistemele binare spectroscopice, metodă utilizată pentru prima oară în 1868 de astronomul britanic William Huggins.[8] Analog, deplasările spre roșu și spre albastru mici detectate în măsurătorile spectroscopice ale unor stele individuale sunt una din modurile în care astronomii au reușit să pună în evidență și să măsoare prezența și caracteristicile sistemelor planetare din jurul altor stele.[49] Măsurătorile deplasărilor spre roșu în detaliu fin sunt utilizate în helioseismologie pentru determinarea cu exactitate a mișcărilor fotosferei Soarelui.[50] Deplasările spre roșu au fost folosite și pentru a realiza prima măsurătoare a perioada de rotație al planetelor,[51] vitezele norilor interstelari,[52] rotația galaxiilor,[2] și dinamica acreției pe stelele neutronice și găurile negre ce prezintă deplasări spre roșu Doppler și gravitaționale.[53] În plus, se pot obține temperaturile diverselor obiecte care emit și absorb lumină măsurând lărgirea Doppler — deplasări spre roșu sau spre albastru pe o singură linie de emisie sau de absorbție.[54] Măsurând lărgirea și deplasarea liniei hidrogenului de 21 cm în direcții diferite, astronomii au reușit să măsoare vitezele de îndepărtare ale gazului interstelar, care la rândul său relevă curba de rotație a Căii Lactee.[2] Au fost efectuate măsurători similare și la alte galaxii, cum ar fi Andromeda.[2] Ca unealtă de diagnosticare, măsurătorile deplasării spre roșu reprezintă una dintre cele mai importante metode de măsurări spectroscopice din astronomie.
Observații extragalactice[modificare | modificare sursă]
Cele mai îndepărtate obiecte prezintă deplasări spre roșu mai pronunțate, corespunzător legii lui Hubble. Cea mai mare deplasare spre roșu observată, corespunzătoare celei mai mari distanțe în spațiu și celui mai îndepărtat moment de timp de emisie, este cel al radiației cosmice de fundal; valoarea numerică a deplasării sale spre roșu este de aproximativ z = 1089 (z = 0 corespunde prezentului), și arată starea Universului cu aproximativ 13,7 miliarde de ani în urmă, la 379.000 de ani după primele momente ale Big Bangului.[55]
Centrele luminoase și punctiforme ale quasarilor au fost primele obiecte cu deplasare mare spre roșu () descoperite înainte ca îmbunătățirea telescoapelor să permită descoperirea galaxiilor cu deplasări mari.
Pentru galaxii din afara Grupului Local și a clusterului Fecioarei din apropiere, la distanțe de maxim câțiva megaparseci, deplasarea spre roșu este aproximativ proporțională cu distanța până la galaxie. Această corelație a fost observată pentru prima oară de Edwin Hubble și este cunoscută sub numele de legea lui Hubble. Vesto Slipher a fost primul care a descoperit deplasări spre roșu ale galaxiilor, în preajma anului 1912, în vreme ce Hubble a corelat măsurătorile lui Slipher cu distanțele pe care le-a măsurat prin alte mijloace pentru a-și formula legea. În modelul cosmologic larg acceptat bazat pe teoria relativității generale, deplasarea spre roșu este în mare parte rezultatul expansiunii spațiului, ceea ce înseamnă că, cu cât o galaxie este mai îndepărtată, cu atât mai mult s-a extins spațiul dintre ea și Pământ din momentul când lumina a plecat de la galaxie, deci cu cât s-a „întins” mai mult lumina, cu atât mai deplasată spre roșu este lumina receptată de noi, și deci cu atât mai rapid pare ea că se îndepărtează. Legea lui Hubble rezultă parțial din principiul copernican.[28] Deoarece de regulă nu se știe cât de luminoase sunt obiectele, măsurarea deplasării spre roșu este mai simplă decât măsurătorile directe ale distanței, deci deplasarea spre roșu este uneori convertită în practică într-o distanță brută folosind legea lui Hubble.
Interacțiunile gravitaționale ale galaxiilor și clusterelor determină o împrăștiere semnificativă a punctelor de pe diagrama lui Hubble. Vitezele galaxiilor se suprapun peste o urmă a masei obiectelor virializate din univers. Acest efect conduce la fenomene cum ar fi deplasarea spre albastru a galaxiilor apropiate (cum ar fi galaxia Andromeda) în căderea spre un baricentru comun, și șabloane de deplasări spre roșu ale unor clustere ce prezintă efectul Degetele lui Dumnezeu datorat împrăștierii vitezelor stranii într-o distribuție aproximativ sferică.[28] Această componentă dă o șansă de a măsura masele obiectelor independent de raportul masă-lumină (raportul dintre masa unei galaxii exprimată în mase solare și luminozitatea sa în luminozități solare), un instrument important de măsurare a materiei întunecate.[56]
Relația liniară a legii lui Hubble între distanță și deplasarea spre roșu presupune că viteza de expansiune a universului ar fi constantă. Când universul era mult mai tânăr, însă, viteza de expansiune, și astfel și „constanta” lui Hubble, erau mai mari decât astăzi. Atunci, pentru galaxiile îndepărtate, a căror lumină călătorește spre noi de mult mai mult timp, aproximarea vitezei constante de expansiune dă greș, iar legea lui Hubble devine o relație integrală neliniară dependentă de istoria vitezei de expansiune de la emisia luminii de la galaxia în chestiune. Observarea relației distanță-deplasare spre roșu se poate, astfel, folosi pentru a determina istoria expansiunii universului și deci conținutul său de materie și energie.
S-a crezut multă vreme că viteza de expansiune a scăzut continuu de la Big Bang, dar observațiile recente asupra relației distanță-deplasare spre roșu la supernovele de tip Ia au sugerat că în vremuri relativ recente viteza de expansiune a universului a început să crească.
Cele mai mari deplasări spre roșu[modificare | modificare sursă]
În prezent, obiectele cu cele mai mari deplasări spre roșu cunoscute sunt galaxiile și obiectele ce produc explozii de radiații gamma. Cele mai sigure date despre deplasarea spre roșu sunt cele spectroscopice, și cea mai mare deplasare spre roșu confirmată spectroscopic la o galaxie este cea a lui IOK-1,[57] cu o deplasare de z = 6,96. Mai puțin sigure sunt deplasările Lyman, dintre care cea mai mare o are galaxia A1689-zD1 cu z = 7,6[58] cea de pe locul doi având [59] iar rapoartele neconfirmate ale lui Ellis R. și alții. dintr-o lentilă gravitațională observate la un cluster îndepărtat de galaxii poate indica o galaxie cu o deplasare spre roșu de .
Cea mai îndepărtată explozie de radiații gamma observată a fost GRB 090423, cu o deplasare spre roșu de 8,2.[60]
Cel mai îndepărtat quasar cunoscut, CFHQS J2329-0301, se află la .[61] Cea mai deplasată galaxie radio (TN J0924-2201) are z = 5,2[62] și cea mai mare deplasare spre roșu a unui material molecular o constituie detecția emisiei moleculelor de CO de pe quasarul SDSS J1148+5251 cu z = 6,42[63]
Obiectele extrem de roșii (ERO) sunt sursele astronomice care radiază energie în zona roșie și cvasiinfraroșie a spectrului electromagnetic. Acestea pot fi galaxii cu stele tinere cu deplasare spre roșu mare însoțită de înroșirea din cauza prafului, sau ar putea fi galaxii eliptice puternic deplasate cu o populație stelară mai bătrână (și deci mai roșie).[64] Obiectel care sunt mai roșii decât ERO sunt denumite „obiecte hiper extrem de roșii” (HERO) .[65]
Studii ale deplasării spre roșu[modificare | modificare sursă]
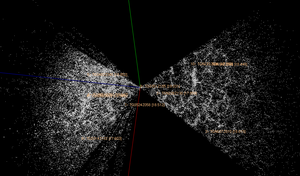
După apariția telescoapelor automate și îmbunătățirile aduse în domeniul spectroscopiei, mai multe colaborări au căutat întocmirea de hărți ale universului în spațiul deplasărilor spre roșu. Combinând deplasarea spre roșu cu datele unghiulare de poziție, un studiu al deplasărilor spre roșu conduce la obținerea unei distribuții 3D a materiei într-o anume parte a cerului. Aceste observații sunt utilizate pentru a măsura proprietățile structurii pe scară largă a universului. Marele Zid, un mare supercluster de galaxii cu o lățime de peste 500 de milioane de ani-lumină, dă un exemplu dramatic de structură pe scară largă pe care o pot detecta studiile deplasării spre roșu.[66]
Primul studiu al deplasării spre roșu a fost CfA Redshift Survey, inițiat în 1977 și a cărui primă perioadă de colectare de date a fost terminată în 1982.[67] Mai recent, 2dF Galaxy Redshift Survey a determinat structura pe scară largă a unei secțiuni a Universului, măsurând valorile z pentru peste 220.000 de galaxii; colectarea datelor s-a încheiat în 2002, iar rezultatele finale au fost publicate la 30 iunie 2003.[68] (Pe lângă cartografierea șabloanelor pe scară largă a galaxiilor, 2dF a stabilit o limită maximă pentru masa neutrinilor.) O altă cercetare notabilă, Sloan Digital Sky Survey (SDSS), fusese început în 2005 și încerca să măsoare peste 100 de milioane de obiecte.[69] SDSS a înregistrat deplasări spre roșu ale unor galaxii de până la 0,4, și s-a ocupat de detecția de quasari cu z mai mare ca 6. DEEP2 Redshift Survey utilizează telescoapele Keck cu noul spectrograf "DEIMOS"; o urmare a programului pilot DEEP1, DEEP2 este gândit pentru a măsura galaxii cu luminozitate mică și cu deplasări de la 0,7 în sus, și urmează, deci, să furnizeze o completare pentru SDSS și 2dF.[70]
Efecte datorate opticii fizice și transferului radiativ[modificare | modificare sursă]
Interacțiunile și fenomenele de transfer radiativ și optică fizică pot avea ca rezultat deplasări ale lungimii de undă și frecvenței radiațiilor electromagnetice. În astfel de cazuri deplasările corespund unui transfer de energie spre materie sau spre alți fotoni în loc de a corespunde unei treceri între sisteme de referință. Aceste deplasări se pot datora unor fenomene fizice cum ar fi efectele de coerență sau Împrăștierea de radiație electromagnetică fie din particule elementare încărcate electric, particule de aerosol, sau fluctuații ale indicelui de refracție într-un mediu dielectric ca în fenomenul radio de „whistler”.[2] Asemenea fenomene sunt și ele denumite deplasări spre roșu sau spre albastru, dar în interacțiunile lumină-materie din astrofizică și care au ca rezultat deplasări de energie în câmpul radiației ele sunt în general denumite „înroșiri” și nu deplasări spre roșu care, ca termen, este rezervat pentru efectele discutate mai sus.[2]
În multe circumstanțe împrăștierea cauzează înroșirea radiației deoarece entropia are ca rezultat predominarea fotonilor de energii joase față de prezența a puțini fotoni de energii înalte (deși energia totală se conservă).[2] Împrăștierea nu produce aceeași schimbare relativă în lungimea de undă în tot spectrul, cu excepția unor experimente efectuate în condiții controlate cu grijă; orice z calculat este în general o funcție de lungimea de undă. Mai mult, împrăștierea cauzată de medii aleatoare are loc la multe unghiuri, iar z este o funcție și de unghiul de împrăștiere. Dacă au loc mai multe împrăștieri, sau particulele împrăștiate au o mișcare relativă, atunci există și o distorsiune a liniilor spectrale.[2]
În astronomia interstelară, spectrul vizibil poate apărea mai roșu din cauza proceselor de împrăștiere într-un fenomen denumit înroșire interstelară[2] — la fel împrăștierea Rayleigh cauzează înroșirea atmosferică dată de Soare la răsărit și la apus și face ca restul cerului să fie albastru. Acest fenomen este diferit de deplasarea spre roșu deoarece liniile spectrale nu sunt deplasate la alte lungimi de undă la obiectele înroșite și în plus există și o slăbire a intensității și o distorsiune asociate cu fenomenul din cauza împrăștierii fotonilor la unghiuri diferite de cel de privire directă.
Note[modificare | modificare sursă]
- ^ Vezi Feynman, Leighton și Sands (1989) sau orice alt manual de fizică de liceu sau de primii ani de facultate. Vezi Taylor (1992) pentru o discuție relativistă.
- ^ a b c d e f g h i j Vezi Binney și Merrifeld (1998), Carroll și Ostlie (1996), Kutner (2003) pentru aplicații în astronomie.
- ^ N.I. Ionescu- Pallas, Relativitate generala și cosmologie, București,Editura științifică și enciclopedică, 1980
- ^ Vezi Misner, Thorne și Wheeler (1973) și Weinberg (1971) sau orice manual de cosmologie fizică
- ^ Doppler, Christian, (1846), Prag, Druck von G. Haase sohne
- ^ Dev Maulik, "Doppler Sonography: A Brief History" în Doppler Ultrasound in Obstetrics And Gynecology (2005) de Dev (EDT) Maulik, Ivica Zalud
- ^ O'Connor, John J.; Robertson, Edmund F., „Deplasare spre roșu”, MacTutor History of Mathematics archive, University of St Andrews.
- ^ a b William Huggins, "Further Observations on the Spectra of Some of the Stars and Nebulae, with an Attempt to Determine Therefrom Whether These Bodies are Moving towards or from the Earth, Also Observations on the Spectra of the Sun and of Comet II." (1868) Philosophical Transactions of the Royal Society of London, Volumul 158, pp. 529–564
- ^ Reber, G., "Intergalactic Plasma"(1995) Astrophysics and Space Science, v. 227, p. 93–96.
- ^ Bélopolsky, A., "On an Apparatus for the Laboratory Demonstration of the Doppler-Fizeau Principle" (1901) Astrophysical Journal, vol. 13, p.15
- ^ Adams, Walter S., "No. 22. Preliminary catalogue of lines affected in sun-spots" (1908) Contributions from the Mount Wilson Observatory / Carnegie Institution of Washington, vol. 22, pp.1–21
- ^ Slipher prezintă pentru prima oară măsurătorile sale în volumul inaugural al Buletinului Observatorului Lowell, pp.2.56-2.57 [1]. În articolul său intitulat The radial velocity of the Andromeda Nebula, el afirmă că a făcut prima măsurătoare Doppler la 17 septembrie 1912. Slipher scria: „Mărimea acestei viteze, care este cea mai mare observată până acum, ridică întrebarea dacă deplasarea aceasta nu este cauzată de altceva, dar eu cred că deocamdată nu avem alte interpretări pentru ea.” După trei ani, în revista Popular Astronomy, Vol. 23, p. 21–24 [2], Slipher a scris un articol intitulat Spectrographic Observations of Nebulae (Observații spectrografice asupra nebuloaselor). El afirma acolo: „Descoperirea anterioară a faptului că marea spirală Andromeda are o viteză excepțională - 300 km(/s) a arătat metodele disponibile atunci, capabile de a cerceta nu doar spectrele spiralelor, ci și vitezele.” Slipher a prezentat vitezele a 15 nebuloase spirale de pe cer, toate în afară de trei având viteze „pozitive”.
- ^ Hubble, Edwin, "A Relation between Distance and Radial Velocity among Extra-Galactic Nebulae" (1929) Proceedings of the National Academy of Sciences of the United States of America, Volume 15, Issue 3, pp. 168–173 (Full article Arhivat în , la Wayback Machine., PDF)
- ^ Friedman, A: Über die Krümmung des Raumes, Z. Phys. 10 (1922), 377–386. (English translation in: Gen. Rel. Grav. 31 (1999), 1991–2000.)
- ^ a b Aceasta a fost recunoscută de la început de fizicieni și astronomi care efectuau cercetări în domeniul cosmologiei în anii 1930. Prima publicație pentru publicul larg în care s-a descris această corespondență în detaliu a fost cartea lui Sir Arthur Eddington The Expanding Universe: Astronomy's 'Great Debate', 1900–1931, publicată la Press Syndicate of the University of Cambridge în 1933.
- ^ Vedeți, de exemplu, acest comunicat de presă din 25 mai 2004 de la telescopul spațial Swift al NASA care cerceta exploziile de radiații gamma: „Măsurătorile spectrelor de radiații gamma obținute în timpul principalei explozii s-au dovedit de prea puțină utilizate ca indicatori ai deplasării spre roșu, din cauza lipsei de caracteristici bine definite. Cu toate acestea, observațiile optice ale strălucirilor de după exploziile de radiații gama au produs spectre cu linii identificabile, ceea ce au dus la măsurători precise ale deplasării spre roșu.”
- ^ Unde z = deplasarea; v|| = viteza paralelă cu direcția privirii (pozitivă dacă se îndepărtează de observator); c = viteza luminii; γ = factorul Lorentz; a = factorul de scalare universală; G = constanta gravitațională; M = masa obiectului; r = coordonata Schwarzschild radială, gtt = Componenta t,t a tensorului metric
- ^ N.I.Ionescu- Pallas, Relativitate generala și cosmologie, paragraf 40, p. 162- 165, București, Ed. Științifică și enciclopedică, 1980
- ^ H. Ives și G. Stilwell, An Experimental study of the rate of a moving atomic clock, J. Opt. Soc. Am. 28, 215–226 (1938) [3]
- ^ Vedeți „Fotoni, relativitate, deplasare Doppler Arhivat în , la Wayback Machine.” la Universitatea Queensland
- ^ Tamara M. Davis, Charles H. Lineweaver (). „Superluminal Recessional Velocities”. ArXiv preprint. arXiv:astro-ph/0011070v2
 .
.
- ^ a b Distincția este clarificată în Edward Robert Harrison (). Cosmology: The Science of the Universe (ed. 2). Cambridge University Press. pp. 306ff. ISBN 052166148X.
- ^ N.I. Ionescu- Pallas,Relativitate generala și cosmologie. Ecartul de frecventa cosmologic, paragraf 88, Universul in expansiune, pp.573-586, București, Editura științifică și enciclopedică, 1980
- ^ Theo Koupelis, Karl F. Kuhn (). In Quest of the Universe (ed. 5). Jones & Bartlett Publishers. p. 557. ISBN 0763743879.
- ^ „Este perfect corect să interpretăm ecuaţiile relativităţii în termeni de spaţiu în expansiune. Greşeala este aceea de a duce analogiile prea departe şi de a atribui spaţiului proprietăţi fizice incompatibile cu ecuaţiile relativităţii.” Geraint F. Lewis; et al. (). „Cosmological Radar Ranging in an Expanding Universe”. Monthly Notices of the Royal Astronomical Society. 388 (3): 960–964. arXiv:0805.2197v1
 . doi:10.1111/j.1365-2966.2008.13477.x.
. doi:10.1111/j.1365-2966.2008.13477.x.
- ^ Michal Chodorowski (). „Is space really expanding? A counterexample”. Concepts Phys. 4: 17–34. arXiv:astro-ph/0601171v2
 .
.
- ^ Aceasta ar fi valabilă doar într-un univers în care nu există „viteze stranii”. Altfel, deplasările spre roșu se combină în forma
- ^ a b c Peebles (1993).
- ^ Măsurători ale vitezelor ciudate ale galaxiilor până la 5 Mpc folosind telescopul spațial Hubble au fost arătate în 2003 de Karachentsev et al. Local galaxy flows within 5 Mpc. 02/2003 Astronomy and Astrophysics, 398, 479-491.[4]
- ^ Steven Weinberg (). The First Three Minutes: A Modern View of the Origin of the Universe (ed. 2). Basic Books. p. 34. ISBN 0465024378.[nefuncțională]
- ^ Lars Bergström, Ariel Goobar (). Cosmology and Particle Astrophysics (ed. 2). Springer. p. 77, Eq.4.79. ISBN 3540329242.
- ^ M.S. Longair (). Galaxy Formation. Springer. p. 161. ISBN 3540637850.
- ^ Yu N Parijskij (). „The High Redshift Radio Universe”. În Norma Sanchez. Current Topics in Astrofundamental Physics. Springer. p. 223. ISBN 0792368568.
- ^ Edward Harrison (). „The redshift-distance and velocity-distance laws”. Astrophysical Journal, Part 1. 403: 28–31. Bibcode:1993ApJ...403...28H. doi:10.1086/172179.. Un fișier pdf poate fi găsit aici.
- ^ Steven Weinberg (). Cosmology. Oxford University Press. p. 11. ISBN 9780198526827.
- ^ Odenwald & Fienberg 1993
- ^ O viteză mai mare decât a luminii este permisă deoarece metrica expansiunii spațiu-timpului este descrisă de relativitatea generală în termeni de șiruri de sisteme de referință inerțiale locale în opoziție cu o metrică Minkowski globală. Expansiunea mai rapidă decât lumina este un efect cumulativ pe mai multe sisteme de referință inerțiale locale și este permisă deoarece nu este implicat un singur sistem de referință inerțial. Limitarea vitezei la viteza luminii se aplică doar local. Vezi Michal Chodorowski (). „Is space really expanding? A counterexample”. Concepts Phys. 4: 17–34. arXiv:astro-ph/0601171v2
 .
.
- ^ M. Weiss, What Causes the Hubble Redshift?, în Physics FAQ (1994), disponibilă pe website-ul lui John Baez
- ^ Vezi de exemplu, Chant, C. A., "Notes and Queries (Telescopes and Observatory Equipment-The Einstein Shift of Solar Lines)" (1930) Journal of the Royal Astronomical Society of Canada, Vol. 24, p.390
- ^ N.I. Ionescu- Pallas, Relativitate generala și cosmologie, Ed. Științifică și cosmologică, B., Paragraf 40, p.162- 165, 1980
- ^ Einstein, A (). „Titlu necunoscut”. Jahrbuch der Radioaktivität und Elektronik. 4: 411–?.
- ^ R. V. Pound și G. A. Rebka Jr., Apparent weight of photons, Phys. Rev. Lett. 4, 337 (1960). [5] Această lucrare prezintă prima măsurătoare.
- ^ Sachs, R. K. (). „Perturbations of a cosmological model and angular variations of the cosmic microwave background”. Astrophysical Journal. 147 (73): 73. doi:10.1086/148982.
- ^ Când s-a descoperit deplasarea cosmologică spre roșu, Fritz Zwicky a propus un efect cunoscut sub numele de „lumină obosită”. Acesta este uneori amintit din rațiuni istorice, dar este, împreună cu ipotezele deplasării intrinseci spre roșu, utilizat în cosmologiile nestandard. În 1981, H. J. Reboul a rezumat numeroasele mecanisme alternative de deplasare spre roșu discutate în literatură din anii 1930. În 2001, Geoffrey Burbidge a remarcat într-o recenzie că larga comunitate astronomică a marginalizat astfel de discuții din anii 1960. Burbidge și Halton Arp, investigând misterul naturii quasarilor, au încercat să dezvolte mecanisme alternative de deplasare spre roșu, dar foarte puțini dintre ceilalți oameni de știință le-au luat în considerare lucrările, și și mai puțini le-au acceptat. Mai mult, Goldhaber et al. 2001; "Timescale Stretch Parameterization of Type Ia Supernova B-Band Lightcurves", ApJ, 558:359-386, 1 septembrie 2001 arată că teoriile alternative nu pot explica întinderea temporală observată la supernovele de tip Ia
- ^ Pentru generalități despre fotometrie, vedeți Budding, E., Introduction to Astronomical Photometry, Cambridge University Press (24 septembrie 1993), ISBN 0-521-41867-4
- ^ Tehnica a fost descrisă pentru prima oară de Baum, W. A.: 1962, în G. C. McVittie (ed.), Problems of extra-galactic research, p. 390, IAU Symposium No. 15
- ^ Bolzonella, M.; Miralles, J.-M.; Pelló, R., Photometric redshifts based on standard SED fitting procedures, Astronomy and Astrophysics, 363, p.476–492 (2000).
- ^ Generalități pedagogice despre corecția K de David Hogg și alți membri ai colaborării SDSS se pot găsi la astro-ph.
- ^ Exoplanet Tracker este cel mai recent proiect ce utilizează această tehnică, fiind capabil să observe variații ale deplasării spre roșu la mai multe obiecte simultan, după cum se arată în Ge, Jian et al. The First Extrasolar Planet Discovered with a New-Generation High-Throughput Doppler Instrument, The Astrophysical Journal, 2006 648, Numărul 1, pp. 683-695.[6]
- ^ Libbrecht, Ken G., Solar and stellar seismology, Space Science Reviews, 1988 37 n. 3–4, 275–301.
- ^ În 1871 Hermann Carl Vogel a măsurat perioada de rotație al lui Venus. Vesto Slipher lucra la asemenea măsurători când și-a îndreptat atenția spre nebuloasele spirale.
- ^ O primă viziune a lui Oort, J. H. asupra subiectului: The formation of galaxies and the origin of the high-velocity hydrogen, Astronomy and Astrophysics, 7, 381 (1970) [7].
- ^ Asaoka, Ikuko, X-ray spectra at infinity from a relativistic accretion disk around a Kerr black hole, Astronomical Society of Japan, Publications (ISSN 0004-6264), 41 no. 4, 1989, p. 763–778 [8]
- ^ Rybicki, G. B. și A. R. Lightman, Radiative Processes in Astrophysics, John Wiley & Sons, 1979, p. 288 ISBN 0-471-82759-2
- ^ O măsurare precisă a radiației cosmice de fundal s-a realizat prin experimentul COBE. Temperatura finală de 2,73 K a fost prezentată în lucrarea: Fixsen, D. J.; Cheng, E. S.; Cottingham, D. A.; Eplee, R. E., Jr.; Isaacman, R. B.; Mather, J. C.; Meyer, S. S.; Noerdlinger, P. D.; Shafer, R. A.; Weiss, R.; Wright, E. L.; Bennett, C. L.; Boggess, N. W.; Kelsall, T.; Moseley, S. H.; Silverberg, R. F.; Smoot, G. F.; Wilkinson, D. T.. (1994). "Cosmic microwave background dipole spectrum measured by the COBE FIRAS instrument", Astrophysical Journal, 420, 445. Cea mai exactă măsurătoare la nivelul anului 2006 fusese realizată prin experimentul WMAP.
- ^ Binney, James (). Galactic dynamics. Princeton University Press. ISBN 0-691-08445-9.
- ^ Masanori Iye; et al. (). „A galaxy at a redshift z = 6.96”. Nature. 443 (7108): 186–188. doi:10.1038/nature05104. PMID 16971942.
- ^ Bradley, L.., et al., Discovery of a Very Bright Strongly Lensed Galaxy Candidate at z ~ 7.6, The Astrophysical Journal (2008), Volumul 678, Numărul 2, pp. 647-654. [http://adsabs.harvard.edu/abs/2008ApJ...678..647B
- ^ Egami, E., et al., Spitzer and Hubble Space Telescope Constraints on the Physical Properties of the z~7 Galaxy Strongly Lensed by A2218, The Astrophysical Journal (2005), v. 618, Numărul 1, pp. L5-L8 [9].
- ^ Salvaterra, R.; et al. (). „GRB 090423 reveals an exploding star at the epoch of re-ionization”. Submitted to Nature. 0906: 1578. arXiv:0906.1578
 . Bibcode:2009arXiv0906.1578S. Parametru necunoscut
. Bibcode:2009arXiv0906.1578S. Parametru necunoscut |class=ignorat (ajutor) - ^ Willott, Chris J. et al., Four Quasars Above Redshift 6 Discovered by the Canada-France High-z Quasar Survey, The Astronomical Journal (2007), v. 134, pp. 2435–2450 [10].
- ^ Klamer et al., 2005, ApJ 621, L1
- ^ Walter, Fabian et al., Molecular gas in the host galaxy of a quasar at redshift z = 6.42, Nature (2003), v. 424, pp. 406–408 [11].
- ^ Smail, Ian; Owen, F. N.; Morrison, G. E.; Keel, W. C.; Ivison, R. J.; Ledlow, M. J. (). „The Diversity of Extremely Red Objects”. The Astrophysical Journal. 581 (2): 844–864. Bibcode:2002ApJ...581..844S. doi:10.1086/344440. Parametru necunoscut
|total=ignorat (ajutor) - ^ Totani, Tomonori; Yoshii, Yuzuru; Iwamuro, Fumihide; Maihara, Toshinori; Motohara, Kentaro (). „Hyper Extremely Red Objects in the Subaru Deep Field: Evidence for Primordial Elliptical Galaxies in the Dusty Starburst Phase”. The Astrophysical Journal. 558 (2): L87–L91. Bibcode:2001ApJ...558L..87T. doi:10.1086/323619.
- ^ M. J. Geller & J. P. Huchra, Science 246, 897 (1989). online
- ^ Vezi site-ul oficial CfA pentru detalii.
- ^ Shaun Cole et al. (The 2dFGRS Collaboration) (). „The 2dF galaxy redshift survey: Power-spectrum analysis of the final dataset and cosmological implications”. Mon. Not. Roy. Astron. Soc. 362: 505–34.[nefuncțională] 2dF Galaxy Redshift Survey homepage Arhivat în , la Wayback Machine.
- ^ SDSS Homepage
- ^ Marc Davis et al. (DEEP2 collaboration) (). „Science objectives and early results of the DEEP2 redshift survey”. Conference on Astronomical Telescopes and Instrumentation, Waikoloa, Hawaii, 22–28 Aug 2002.
Bibliografie[modificare | modificare sursă]
Articole[modificare | modificare sursă]
- Odenwald, S. & Fienberg, RT. 1993; "Galaxy Redshifts Reconsidered" în Sky & Telescope Feb. 2003; pp31–35 (Acest articol este util ca lectură suplimentară pentru diferențele între cele trei tipuri de deplasare spre roșu și cauzele lor.)
- Lineweaver, Charles H. și Tamara M. Davis, "Misconceptions about the Big Bang", Scientific American, martie 2005. (Acest articol este util pentru explicarea mecanismului deplasării spre roșu cosmologice, ca și pentru clarificarea unor concepții greșite în ce privește fizica extinderii universului.)
Cărți[modificare | modificare sursă]
- Binney, James (). Galactic Astronomy. Princeton University Press. ISBN 0-691-02565-7.
- Carroll, Bradley W. and Dale A. Ostlie (). An Introduction to Modern Astrophysics. Addison-Wesley Publishing Company, Inc. ISBN 0-201-54730-9.
- Feynman, Richard; Leighton, Robert; Sands, Matthew (). Feynman Lectures on Physics. Vol. 1. Addison-Wesley. ISBN 0-201-51003-0.
- Grøn, Øyvind (). Einstein's General Theory of Relativity. New York: Springer. ISBN 978-0-387-69199-2.
- Kutner, Marc (). Astronomy: A Physical Perspective. Cambridge University Press. ISBN 0-521-52927-1.
- Misner, Charles (). Gravitation. San Francisco: W. H. Freeman. ISBN 0-7167-0344-0.
- Peebles, P. J. E. (). Principles of Physical Cosmology. Princeton University Press. ISBN 0-691-01933-9.
- Taylor, Edwin F.; Wheeler, John Archibald (). Spacetime Physics: Introduction to Special Relativity (2nd ed.). W.H. Freeman. ISBN 0-7167-2327-1.
- Weinberg, Steven (). Gravitation and Cosmology. John Wiley. ISBN 0-471-92567-5.
Legături externe[modificare | modificare sursă]
- Tutorial de cosmologie de Ned Wright
- Articol despre deplasarea spre roșu de la SPACE.com
- Deplasarea spre roșu într-un glosar astronomic Arhivat în , la Wayback Machine.
- Tutorial de deplasare spre roșu de Mike Luciuk Arhivat în , la Wayback Machine.
- GIF animat al deplasării spre roșu cosmologice de Wayne Hu























































