Pavare cu dreptunghiuri
În geometrie o pavare cu dreptunghiuri este o pavare cu dale dreptunghiulare. Pavarea domino are dalele în formă de dreptunghiuri cu laturile în raportul de 1 × 2. Pavările cu poliominouri drepte de formele 1 × 3, 1 × 4, precum și pavările cu poliominouri de forma 2 × 3 fac parte și ele din această categorie.
Pavări cu dreptunghiuri congruente[modificare | modificare sursă]
Exemple de pavări cu dreptunghiuri congruente:
|

|

|

|

|
| Stivă de cărămizi | Perete de cărămidă | Împletitură de coș | Împletitură de coș | Parchet oblic |
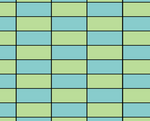
Pavarea de tip „stivă de cărămizi” este topologic o pavare pătrată, scalată de-a lungul unei laturi. Raportul lungimilor laturilor poate avea orice valoare.
Pavarea de tip „perete de cărămidă” este topologic o pavare hexagonală degenerată unde în două perechi neadiacente de laturi cele două laturi adiacente care formează perechea devin coliniare. Și aici raportul lungimilor laturilor poate avea orice valoare.
La pavările de tip „împletitură de coș” și „parchet oblic” raportul dintre lungimea laturii lungi și a celei scurte trebuie să fie un număr rațional (uzual, un număr natural).
Pavări cu dreptunghiuri necongruente[modificare | modificare sursă]

O pavare cu dreptunghiuri necongruente se poate obține prin scalarea pe una din laturi a oricărei pavări cu pătrate necongruente, de exemplu a unei pavări pitagoreice.
Un exemplu de pavare cu dreptunghiuri necongruente arbitrare este teselarea Gilbert în varianta cu laturile paralele cu axele.[1]
Cel mai mic pătrat care poate fi tăiat în dreptunghiuri (m × n), astfel încât toate m și n să fie numere întregi diferite, este pătratul de 11 × 11, iar pavarea folosește cinci dreptunghiuri.[2]
Cel mai mic dreptunghi care poate fi tăiat în dreptunghiuri (m × n), astfel încât toate m și n să fie numere întregi diferite, este dreptunghiul de 9 × 13, iar pavarea folosește cinci dreptunghiuri.[2][3]
Note[modificare | modificare sursă]
- ^ en Schreiber, Tomasz; Soja, Natalia (), Limit theory for planar Gilbert tessellations, arXiv:1005.0023
 , Bibcode:2010arXiv1005.0023S
, Bibcode:2010arXiv1005.0023S
- ^ a b en Madachy, Joseph S. (). „Solutions to Problems and Conjectures”. Journal of Recreational Mathematics. 29 (1): 73. ISSN 0022-412X.
- ^ en Herringbone Tiles on a Bathroom Wall


