Metrică
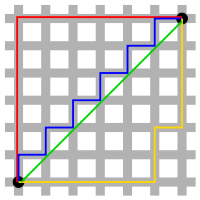
În matematică, o metrică sau funcție distanță este o funcție care definește o distanță(d) între fiecare pereche de elemente ale unei mulțimi. O mulțime împreună cu o metrică asociată formează un spațiu metric. Metrica induce o topologie pe mulțime, dar nu toate topologiile pot fi generate de o metrică. Un spațiu topologic a cărui topologie poate fi descrisă de o metrică se numește metrizabil(d).
O sursă importantă de metrici în geometria diferențială o constituie tensorii metrici(d), forme biliniare care pot fi definite pe vectorii tangenți(d) ai unei varietăți diferențiabile(d), pe un scalar. Un tensor metric permite ca distanțele de-a lungul curbelor să fie determinate prin integrare și determină astfel o metrică. Cu toate acestea, nu orice metrică provine de la un tensor metric în acest fel.
Definiție
[modificare | modificare sursă]O metrică pe o mulțime X este o funcție (numită funcție distanță sau pur și simplu distanță)
Unde este mulțimea numerelor reale nenegative și pentru orice , sunt îndeplinite următoarele condiții:
Condiția 1, împreună cu faptul că d are valoare nenegative, definește o funcție pozitiv definită(d); condiția 2 definește o funcție simetrică; Condiția 3 se numește inegalitatea triunghiului.
O metrică se numește ultrametrică(d) dacă satisface următoarea versiune mai puternică a inegalității triunghiului în care punctele nu pot cădea niciodată „între” alte puncte:
pentru orice
O metrică d peste X se numește intrinsecă(d) dacă oricare două puncte x și y din X pot fi unite printr-o curbă cu lungime arbitrar apropiată de d(x, y) .
Pentru mulțimile pe care se definește o adunare + : X × X → X, d se numește metrică invariantă la translație dacă
pentru orice x , y și a din X
Observații
[modificare | modificare sursă]Aceste condiții exprimă noțiuni intuitive despre conceptul de distanță(d). De exemplu, distanța dintre două puncte distincte este pozitivă, iar distanța de la x la y este aceeași cu distanța de la y la x. Inegalitatea triunghiului înseamnă că distanța de la x la z prin y este cel puțin la fel de mare ca de la x la z direct. Euclid, în lucrarea sa, afirma că cea mai mică distanță între două puncte este o linie; aceasta era inegalitatea triunghiului pentru geometria sa.
Exemple
[modificare | modificare sursă]- Metrica discretă(d): dacă x = y atunci d(x,y ) = 0. În caz contrar, d(x,y) = 1.
- Metrica euclidiană este invariantă la translație și rotație.
- Metrica taximetristului este invariantă la translație.
- Mai general, orice metrică indusă de o normă este invariantă la translație.
- Dacă este un șir de seminorme care definesc un spațiu vectorial topologic(d) (local convex(d)) E , atunci
- este o metrică care definește aceeași topologie. (Se poate înlocui cu orice șir sumabil(d) de numere strict pozitive(d).)
- Metrica grafului(d), o metrică definită în termeni de distanțe într-un anumit graf.
- Distanța Hamming în teoria codării.
- Metrica riemanniană(d), un tip de funcție metrică adecvată spre aplicarea în orice varietate diferențiabilă(d). Pentru orice astfel de varietate, se alege în fiecare punct p o forma biliniară simetrică, pozitiv definită L: T p × T p → ℝ pe spațiul tangent(d) Tp în p, făcând acest lucru într-o manieră continuă. Această formă determină lungimea oricărui vector tangent v pe varietate, prin definiția || v || = √L(v, v) . Apoi, pentru orice drum diferențiabil pe varietate, lungimea sa este definită ca integrală a lungimii vectorului tangent la drum în orice punct, unde integrarea se face în raport cu parametrul drumului. În cele din urmă, pentru a obține o valoare definită pe orice pereche {x, y} de puncte din varietate, se ia infimum din toate drumurile de la x la y, din mulțimea de lungimi ale drumurilor. O varietate netedă echipată cu o metrică riemanniană se numește varietate riemanniană(d).
- Metrica Fubini-Study(d) pe un spațiu proiectiv complex(d). Acesta este un exemplu de metrică riemanniană.
- Metrici pe șiruri de caractere(d), cum ar fi distanța Levenshtein(d) și alte distanțe de editare a șirurilor(d), definesc o metrică peste șirurile de caractere(d).
- Distanța de editare a grafurilor(d) definește o funcție de distanță între grafuri.
- Metrica Wasserstein(d) este o funcție de distanță definită între două distribuții de probabilități.
- Metrica Finsler(d) este o funcție nenegativă continuă F: TM → [0, + ∞) definită pe mănunchiul tangent.
Echivalența metricilor
[modificare | modificare sursă]Pentru o mulțime dată X, două metrici d1 și d2 se numesc echivalente topologic (uniform echivalente) dacă aplicația identitate
- id: (X, d 1) → (X, d 2)
este un homeomorfism(d) (izomorfism uniform(d)).
De exemplu, dacă d este o metrică, atunci min(d, 1) și sunt metrici echivalente cu d.
Metrici pe spații vectoriale
[modificare | modificare sursă]Normele spațiilor vectoriale sunt echivalente cu anumite metrici, și anume cele omogene, invariante la translație. Cu alte cuvinte, orice normă determină o metrică, și unele metrici determină norme.
Dat fiind un spațiu vectorial normat se poate defini o metrică pe X prin
- .
Metrica d se spune că este indusă de norma .
În schimb, dacă o metrică d pe un spațiu vectorial X satisface proprietățile
- (invarianță la translație)
- (omogenitate)
atunci putem defini o normă pe X prin
Analog, o seminormă induce o pseudometrică (vezi mai jos), iar o pseudometrică omogenă și invariabilă la translație induce o seminormă.
Metrici pe multimulțimi
[modificare | modificare sursă]Se poate generaliza noțiunea de metrică de la o distanță între două elemente la o distanță între două multimulțimi finite nevide de elemente. O multimulțime este o generalizare a noțiunii de mulțime astfel încât un element să poată apărea de mai multe ori. Se definește dacă Z este multimulțimea formată din elementele multimulțimilor X și Y, adică dacă x apare o dată în X și o dată în Y, atunci apare de două ori în Z. O funcție distanță d pe mulțimea de multimulțimi finite este o metrică [1] dacă
- dacă toate elementele lui X sunt egale și altfel (pozitiv-definitudine(d)), adică (nenegativitate(d) plus identitatea indiscernibilelor(d))
- d(X)este invariabilă în toate permutațiile lui X (simetrie)
- (inegalitatea triunghiului)
Se observă că metrica familiară dintre două elemente rezultă dacă multimulțimea X are două elemente în 1 și 2 și mulțimile X, Y, Z au fiecare câte un element în 3. De exemplu, dacă X este formată din două apariții ale lui x, atunci conform punctului 1.
Un exemplu simplu este mulțimea tuturor multimulțimilor finite nevide X de numere întregi cu . Exemple mai complexe sunt distanța de informație(d) în multimulțimi; [1] și distanța de compresie normalizată(d) (NCD) în multimulțimi.[2]
Metrici generalizate
[modificare | modificare sursă]Există numeroase moduri de a relaxa axiomele metricilor, dând naștere la diferite noțiuni de spații metrice generalizate. Aceste generalizări pot fi și combinate. Terminologia utilizată pentru a le descrie nu este însă complet standardizată. Mai ales, în analiza funcțională(d), pseudometricile provin adesea din seminorme pe spații vectoriale, deci este natural să fie numite „semimetrici”. Acest lucru este în conflict cu utilizarea termenului în topologie.
Metrici extinse
[modificare | modificare sursă]Unii autori permitca funcția distanță d să atingă valoarea ∞, adică distanțele să fie numere nenegative axa numerelor reale extinsă. O astfel de funcție se numește metrică extinsă sau „∞-metrică”. Fiecare metrică extinsă poate fi transformată într-o metrică finită astfel încât spațiile metrice să fie echivalente în ceea ce privește noțiunile de topologie (cum ar fi continuitatea sau convergența). Acest lucru se poate face cu ajutorul unei funcții subaditive(d) monoton crescătoare mărginită care este zero în zero, de exemplu sau .
Cerința ca valorile metrice să ia valori în [0, ∞) poate fi chiar relaxată pentru a lua în considerare valorile măsurate în alte mulțimi orientate(d). Reformularea axiomelor în acest caz conduce la construirea unor spații uniforme(d): spații topologice cu o structură abstractă care să permită compararea topologiilor locale ale diferitelor puncte.
Pseudometrici
[modificare | modificare sursă]O pseudometrică pe X este o funcție care satisface axiomele unei metrici, cu excepția faptului că în locul celei de a doua (identitatea indiscernibilelor) este obligatoriu numai ca d(x,x) = 0 pentru orice x. Cu alte cuvinte, axiomele unei pseudometrici sunt:
- d(x,y) ≥ 0
- d(x,x) = 0 (dar posibil d(x,y) = 0 și pentru unele valori distincte x ≠ y)
- d(x,y) = d(y,x)
- d(x,z) ≤ d(x,y) + d(y,z).
În unele contexte, pseudometricile sunt denumite semimetrici din cauza relației lor cu seminormele.
Cvasimetrici
[modificare | modificare sursă]Ocazional, o cvasimetrică este definită ca o funcție care satisface toate axiomele unei metrici cu o eventuală excepție a simetriei.[3][4] Numele acestei generalizări nu este complet standardizat.[5]
- d(x,y) ≥ 0 (pozitivitate)
- d(x,y ) = 0 dacă și numai dacă x = y (pozitiv-definitudine)
d(x,y) = d(y,x)(simetrie , abandonată)- d(x,z) ≤ d(x,y) + d(y,z) (inegalitatea triunghiului)
Cvasimetricile sunt obișnuite în viața reală. De exemplu, dată fiind o mulțime X de sate de munte, timpii tipici de mers pe jos între elementele lui X formează o cvasi-metrică, deoarece călătoria ka vale durează mai mult decât călătoria la deal. Un alt exemplu este reprezentat de o topologie a geometriei taximetristului, cu străzi cu sens unic, unde un drum de la punctul A la punctul B cuprinde o mulțime diferită de străzi decât un drum de la B la A.
O cvasimetrică pe numerele reale se poate defini fixând
- d(x,y) = x - y dacă x ≥ y și
- d(x,y) = 1 altfel. 1 poate fi înlocuit cu infinit sau cu 1 + 10(y-x).
Spațiul topologic care stă la baza acestui spațiu cvasimetric este linia Sorgenfrey(d). Acest spațiu descrie procesul de pilire(d) a unui baston metalic: este ușor de redus dimensiunea, dar este dificil sau imposibil de crescut.
Dacă d este o cvasimetrică pe X, o metrică d' pe X poate fi formată luând
Metametrici
[modificare | modificare sursă]Într-o metametrică, toate axiomele unei metrici sunt îndeplinite, cu excepția faptului că distanța dintre punctele identice nu este neapărat zero. Cu alte cuvinte, axiomele unei metametrici sunt:
- d(x,y) ≥ 0
- d(x,y ) = 0 implică x = y (dar nu și invers)
- d(x,y) = d(y,x)
- d(x,z) ≤ d(x,y) + d(y,z).
Metametricile apar în studiul spațiilor metrice hiperbolice Gromov(d) și al frontierelor lor. Metametrica vizuală pe un astfel de spațiu satisface condiția d(x, x) = 0 pentru punctele x de pe frontieră, dar în caz contrar d(x, x) este aproximativ distanța de la x la frontieră. Metametricile au fost definite pentru prima dată de Jussi Väisälä.[6]
Semimetricile
[modificare | modificare sursă]O semimetrică pe X este o funcție care satisface primele trei axiome, dar nu neapărat și inegalitatea triunghiului:
- d(x,y) ≥ 0
- d(x,y ) = 0 dacă și numai dacă x = y
- d(x,y) = d(y,x)
Unii autori lucrează cu o formă mai relaxată a inegalității triunghiului, cum ar fi:
- (inegalitatea triunghiului ρ-relaxată)
- (inegalitate ρ-inframetrică).
Inegalitatea ρ-inframetrică implică inegalitatea triunghiului ρ-relaxată (presupunând prima axiomă), iar inegalitatea trianghiului ρ-relaxată implică inegalitatea 2ρ-inframetrică. Semimetrica care satisface aceste condiții echivalente a fost uneori denumită „cvasimetrică,[7] „aproape-metrică”[8] sau inframetrică.[9]
Inegalitățile ρ-inframetrice au fost introduse pentru a modela timpii de întârziere dus-întors(d) pe Internet.[9] Inegalitatea triunghiului implică inegalitatea 2-inframetrică, iar inegalitatea ultrametrică(d) este exact inegalitatea(d) 1-inframetrică.
Premetrici
[modificare | modificare sursă]Relaxarea ultimelor trei axiome duce la noțiunea de premetrică, adică o funcție care îndeplinește următoarele condiții:
Acesta nu este un termen standard. Uneori este folosit pentru a se referi la alte generalizări de metrici, cum ar fi pseudosemimetrica[10] sau pseudometrica;[11] în traducerile cărților rusești uneori apare menționată drept „prametrică”.[12]
Orice premetrică dă naștere la o topologie după cum urmează. Pentru un r real pozitiv, r-bila cu centrul într-un punct p este definită ca
O mulțime se numește deschisă dacă pentru orice punct p din mulțime există o r-bilă centrată în p care este conținută în mulțime. Orice spațiu premetric este un spațiu topologic și, de fapt, un spațiu secvențial(d). În general, r-bilele nu trebuie să fie mulțimi deschise în raport cu această topologie. În ceea ce privește metricile, distanța dintre două mulțimi A și B este definită ca
Aceasta definește o premetrică asupra mulțimii de puteri(d) a unui spațiu premetric. Dacă începem cu un spațiu (pseudosemi-)metric, obținem o pseudosemimetrică, adică o premetrică simetrică. Orice premetrică dă naștere unui operator de pre-închidere(d) cl după cum urmează:
Pseudocvasimetrici
[modificare | modificare sursă]Prefixele pseudo-, cvasi- și semi- pot fi de asemenea combinate, de exemplu, o pseudocvasimetrică (uneori numită hemimetrică) relaxează atât axioma indiscernibilității cât și axioma simetriei și este pur și simplu o premetrică care satisface inegalitatea triunghiului. Pentru spațiile pseudocvasimetrice, r-bilele deschise formează o bază de mulțimi deschise. Un exemplu foarte simplu de spațiu pseudocvasimetric este mulțimea {0,1} cu premetrica dată de d(0,1) = 1 și d(1,0) = 0. Spațiul topologic asociat este spațiul Sierpiński(d).
Mulțimile echipate cu o pseudocvasimetrică extinsă au fost studiate de William Lawvere ca „spații metrice generalizate”.[13][14] Din punct de vedere categoric, spațiile pseudometrice extinse și spațiile extinse pseudocvasimetrice, împreună cu aplicațiile lor neexpansive corespunzătoare, au cele mai bune comportamente dintre categoriile spațiului metric. Se pot lua produse și coproduse arbitrare și se pot forma obiecte în cadrul categoriei date. Dacă se renunță la „extins”, se pot lua numai produse și coproduse finite. Dacă se renunță la „pseudo”, nu se mai pot forma obiecte. Spațiile de abordare(d) reprezintă o generalizare a spațiilor metrice care păstrează aceste proprietăți categorice bune.
Cazuri importante de metrici generalizate
[modificare | modificare sursă]În geometria diferențială, se consideră un tensor metric(d), care poate fi văzut ca o funcție metrică „infinitezimală” pătratică. Aceasta este definită ca o formă bilineară simetrică nedegenerată pe spațiul tangent(d) al unei varietăți cu o cerință adecvată de diferențiabilitate. Deși acestea nu sunt funcții metrice așa cum sunt definite în acest articol, ele induc ceea ce se numește o funcție pseudo-semimetrică prin integrarea rădăcinii pătrate de-a lungul unui drum prin varietate. Dacă se impune cerința de pozitiv-definitudine a unui produs scalar pe tensorul metric, acest lucru se limitează la cazul unei varietăți riemanniene(d), iar integrarea pe drum produce o metrică.
În relativitatea generală, conceptul conex este de tensor metric (relativitatea generală) care exprimă structura unei varietăți pseudoriemanniene(d). Deși termenul „metrică” este folosit în cosmologie, ideea fundamentală este diferită deoarece există vectori nuli ne-zero în spațiul tangent al acestor varietăți. Această viziune generalizată a „metricilor” în care distanța zero nu implică identitate, s-a strecurat și în scrierea matematică.[15][16]
Note
[modificare | modificare sursă]- ^ a b Vitanyi, Paul M. B. (). „Information Distance in Multiples”. IEEE Transactions on Information Theory. 57 (4): 2451. doi:10.1109/TIT.2011.2110130.
- ^ Cohen, Andrew R.; Vitanyi, Paul M. B. (). „Normalized Compression Distance of Multisets with Applications”. IEEE Transactions on Pattern Analysis and Machine Intelligence. 37 (8): 1602–1614. doi:10.1109/TPAMI.2014.2375175.
- ^ E.g. Steen & Seebach (1995).
- ^ Smyth, M. (). M.Main, ed. Quasi uniformities: reconciling domains with metric spaces. 3rd Conference on Mathematical Foundations of Programming Language Semantics. Springer-Verlag, Lecture Notes in Computer Science 298. pp. 236–253.
- ^ Rolewicz, Stefan (), Functional Analysis and Control Theory: Linear Systems, Springer, ISBN 90-277-2186-6, OCLC 13064804 Această carte le spune „semimetrici”. Același termen este frecvent folosit și pentru alte două generalizări ale metricilor.
- ^ Väisälä, Jussi (), „Gromov hyperbolic spaces” (PDF), Expositiones Mathematicae, 23 (3): 187–231, doi:10.1016/j.exmath.2005.01.010, MR 2164775
- ^ Xia, Q. (), „The Geodesic Problem in Quasimetric Spaces”, Journal of Geometric Analysis, 19 (2): 452–479, arXiv:0807.3377
 , doi:10.1007/s12220-008-9065-4
, doi:10.1007/s12220-008-9065-4
- ^ Qinglan Xia (), „The geodesic problem in nearmetric spaces”, Journal of Geometric Analysis, 19 (2): 452–479, arXiv:0807.3377
 , Bibcode:2008arXiv0807.3377X.
, Bibcode:2008arXiv0807.3377X.
- ^ a b Fraigniaud, P.; Lebhar, E.; Viennot, L. (). „The Inframetric Model for the Internet”. 2008 IEEE INFOCOM - The 27th Conference on Computer Communications. IEEE INFOCOM 2008. the 27th Conference on Computer Communications. pp. 1085–1093. doi:10.1109/INFOCOM.2008.163. ISBN 978-1-4244-2026-1.Fraigniaud, P.; Lebhar, E.; Viennot, L. (). „The Inframetric Model for the Internet”. 2008 IEEE INFOCOM - The 27th Conference on Computer Communications. IEEE INFOCOM 2008. the 27th Conference on Computer Communications. pp. 1085–1093. doi:10.1109/INFOCOM.2008.163. ISBN 978-1-4244-2026-1..
- ^ Buldygin, V.V.; Kozachenko, I.U.V. (), Metric characterization of random variables and random processes.
- ^ Khelemskiĭ (), Lectures and exercises on functional analysis.
- ^ Arkhangel'skii & Pontryagin (1990). Aldrovandi, R.; Pereira, J.G. (), An introduction to geometrical physics.
- ^ Lawvere, F.W. () [1973], Metric spaces, generalised logic, and closed categories, Reprints in Theory and Applications of Categories, 1, pp. 1–37.
- ^ Vickers, Steven (), „Localic completion of generalized metric spaces I”, Theory and Applications of Categories, 14: 328–356
- ^ S. Parrott (1987) Relativistic Electrodynamics and Differential Geometry, page 4, Springer-Verlag ISBN: 0-387-96435-5 : "This bilinear form is variously called the Lorentz metric, or Minkowski metric or metric tensor."
- ^ Thomas E. Cecil (1992) Lie Sphere Geometry, page 9, Springer-Verlag ISBN: 0-387-97747-3 : "We call this scalar product the Lorentz metric"
Bibliografie
[modificare | modificare sursă]- General Topology I: Basic Concepts and Constructions Dimension Theory,
- Counterexamples in Topology(d),






































