Paralelipiped
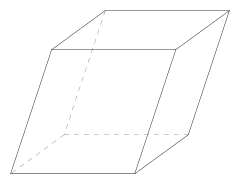
Un paralelipiped este o figură geometrică tridimensională formată din șase paralelograme ce aparțin unor trei perechi de plane paralele. Este o prismă patrulateră, un caz particular de prismă. Având 6 fețe, este un hexaedru.
Proprietăți[modificare | modificare sursă]
- fețele opuse sunt paralele;
- fețele sunt paralelograme;
- cele 12 laturi sunt congruente în serii de câte patru.
Arii[modificare | modificare sursă]
- .
- unde L este lungimea, iar l lățimea bazei.
Aria laterală - Al - se calculează cu relația:
- .
- unde h este înălțimea paralelipipedului.
Aria totală - At - reprezintă suma dintre aria laterală și dublul ariei bazei:
- .
Dacă se înlocuiește aria laterală și aria bazei în formula de mai sus, se obține formula ariei totale a paralelipipedului:
- .
Volumul paralelipipedului este egal cu aria bazei înmulțită cu înălțimea:
- .
Generalizare[modificare | modificare sursă]
Coxeter a denumit generalizarea unui paralelipiped în dimensiuni mai mari drept paralelotop. În literatura modernă, expresia „paralelipiped” este adesea folosită și în dimensiuni mai mari.[1]
Mai exact, în spațiul n-dimensional se numește paralelotop n-dimensional sau n-paralelotop (sau n-paralelipiped). Astfel, un paralelogram este un 2-paralelotop iar un paralelipiped este un 3-paralelotop.
În general, un paralelotop,[2] sau paralelotop voronoi, are fațete opuse paralele și congruente. Deci un 2-paralelotop este un paralelogon, noțiune care poate cuprinde și anumite hexagoane, iar un 3-paralelotop este un paraleloedru, existând 5 tipuri de astfel de poliedre.
Note[modificare | modificare sursă]
- ^ en Morgan, C. L. (1974). Embedding metric spaces in Euclidean space. Journal of Geometry, 5(1), 101–107. https://doi.org/10.1007/bf01954540
- ^ en Deza, Michel; Grishukhin, Viacheslav (). „Properties of parallelotopes equivalent to Voronoi's conjecture”. arXiv:math/0307170
 . Bibcode:2003math......7170D.
. Bibcode:2003math......7170D.
Vezi și[modificare | modificare sursă]
| |||||||||||||||||||||||||||




![{\displaystyle A_{t}=2[(L+l)\cdot {h}+L\cdot {l})]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4130c80fc7a19716d79298e3b30d554b1a8d49b6)



