Duoprismă

P-q duoprisme uniforme
Tip	4-politopuri uniforme prismatice
Simbol Schläfli	{p}×{q}
Diagramă Coxeter
Celule	prisme p q-gonale, prisme q p-gonale
Fețe	pq pătrate, p q-goane, q p-goane
Laturi	2pq
Vârfuri	pq
Figura vârfului	bisfenoid
Grup de simetrie	[p,2,q], de ordinul 4pq
Dual	p-q duopiramidă
Proprietăți	convex, uniform pe vârfuri

P-p duoprisme uniforme
Tip	4-politopuri uniforme prismatice
Simbol Schläfli	{p}×{p}
Diagramă Coxeter
Celule	prisme 2p p-gonale
Fețe	p² pătrate, 2p p-goane
Laturi	2p²
Vârfuri	p²
Grup de simetrie	[p,2,p] = [2p,2⁺,2p] de ordinul 8p²
Dual	p-p duopiramidă
Proprietăți	convex, uniform pe vârfuri, tranzitiv pe fețe

În geometria cvadridimensională sau din dimensiuni superioare o duoprismă este un politop rezultat din produsul cartezian a două politopuri, fiecare cu două dimensiuni sau mai mult. Produsul cartezian al unui politop $n$ -dimensional și al unui politop $m$ -dimensional este un politop ( $n+m$ )-dimensional, unde $n$ și $m$ sunt 2-politopuri (poligoane) sau din dimensiuni mai mari.

Cele mai jos dimensionale duoprisme există în spațiul cvadridimensional ca 4-politopuri fiind produsul cartezian a două poligoane din spațiul euclidian bidimensional. Mai precis, este mulțimea de puncte:

P_{1}\times P_{2}=\{(x,y,z,w)|(x,y)\in P_{1},(z,w)\in P_{2}\}

unde P₁ și P₂ sunt mulțimile punctelor din poligoanele respective. O astfel de duoprismă este convexă dacă ambele baze sunt convexe și este mărginită de celule prismatice.

Denumiri

Duoprismele cvadridimensionale sunt considerate a fi 4-politopuri prismatice. o duoprismă construită din două poligoane regulate cu aceeași lungime a laturilor este o duoprismă uniformă.

O duoprismă formată din $n$ -goane și $m$ -goane este denumită „duoprismă” urmată de numele poligoanelor de bază, de exemplu: o „duoprismă triunghiulară-pentagonală” este produsul cartezian al unui triunghi și al unui pentagon. O alternativă este notația cu un prefix cu numerele laturilor poligoanelor de bază, de exemplu „3-5 duoprismă” sau „3,5 duoprismă” pentru duoprisma triunghiulară-pentagonală.

Nume alternative:

prismă q-gonală-p-gonală
prismă dublă q-gonală-p-gonală
hiperprismă q-gonală-p-gonală

Termenul de duoprismă a fost introdus de George Olshevsky, ca prescurtare la „prismă dublă”. John Horton Conway a propus un nume similar, proprismă, pentru „prismă de produs”, un produs cartezian a două sau mai multe politopuri cel puțin bidimensionale. Duoprismele sunt proprisme formate din exact două politopuri.

Exemplu de 16-16 duoprismă


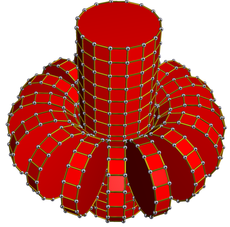
Diagramă Schlegel a unei 16-16 duoprisme, prezentând toate prismele 16-gonale, mai puțin una		Desfășurata. Sunt prezentate cele două seturi de prisme 16-gonale. Fețele de sus și de jos ale cilindrului vertical sunt conectate atunci când sunt pliate împreună în spațiul cvadridimensional.

Geometria duoprismelor cvadridimensionale

O duoprismă uniformă cvadridimensională este creată de produsul unui poligon regulat cu $n$ laturi cu un alt poligon, cu $m$ laturi de aceeași lungime. Este mărginită de $n$ prisme $m$ -gonale și $m$ prisme $n$ -gonale. De exemplu, produsul cartezian al unui triunghi și al unui hexagon este o duoprismă delimitat de 6 prisme triunghiulare și 3 prisme hexagonale.

Când $m$ și $n$ sunt identice, duoprisma rezultată este mărginită de 2 $n$ prisme identice $n$ -gonale. De exemplu, produsul cartezian a două triunghiuri este o duoprismă delimitată de 6 prisme triunghiulare.
Când $m$ și $n$ sunt identice și au valoarea 4, duoprisma rezultată este mărginită de 8 prisme pătrate (cuburi) și este identică cu tesseractul.

Prismele $m$ -gonale sunt atașate între ele prin fețele lor $m$ -gonale și formează o buclă închisă. Similar, prismele $n$ -gonale sunt atașate între ele prin fețele lor $n$ -gonale și formează o a doua buclă, perpendiculară pe prima. Aceste două bucle sunt atașate una de cealaltă prin fețele lor și sunt reciproc perpendiculare.

Pe măsură ce $m$ și $n$ se apropie de infinit, duoprismele corespunzătoare se apropie de un duocilindru. Ca atare, duoprismele sunt utile ca aproximări necuadrice ale duocilindrului.

Desfășurate

3-3	4-4	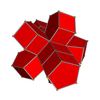5-5	6-6	8-8	10-10
3-4	3-5	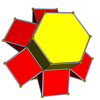3-6	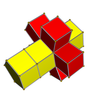4-5	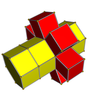4-6	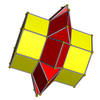3-8

Proiecții în perspectivă

Diagrame Schlegel

O prismă hexagonală proiectată pe un plan în perspectivă, centrată pe o față hexagonală, arată ca un hexagon dublu conectat prin „pătrate” (distorsionate)

O 6-6 duoprismă proiectată în 3D aproximează un tor, hexagonal atât în plan cât și în secțiune

O proiecție în perspectivă cu o celulă în față face ca o duoprismă să arate ca un tor, cu două seturi de celule ortogonale, prisme $p$ -gonale și $q$ -gonale.

Duoprismele p-q sunt identice cu duoprismele q-p, dar arată diferit în aceste proiecții, deoarece proiecțiile sunt centrate pe celule de tip diferit.

Diagrame Schlegel
3-3	3-4	3-5	3-6	3-7	3-8
4-3	4-4	4-5	4-6	4-7	4-8
5-3	5-4	5-5	5-6	5-7	5-8
6-3	6-4	6-5	6-6	6-7	6-8
7-3	7-4	7-5	7-6	7-7	7-8
8-3	8-4	8-5	8-6	8-7	8-8

Proiecții ortogonale

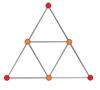
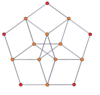
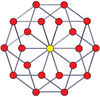
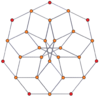
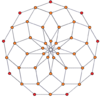
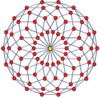
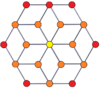
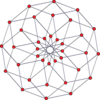
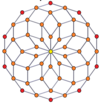
Proiecțiile ortogonale centrate pe vârfuri ale duoprismelor p-p se proiectează în [2 $n$ ] simetrie pentru grade impare și [ $n$ ] pentru grade pare. Există $n$ vârfuri proiectate în centru. Pentru 4,4, reprezintă planul A³ Coxeter al tesseractului. Proiecția 5-5 este identică cu a triacontaedrului rombic.

Proiecții ortogonale „cadru de sârmă” ale duoprismelor p-p
Impare
3-3		5-5		7-7		9-9

[3]	[6]	[5]	[10]	[7]	[14]	[9]	[18]
Pare
4-4 (tesseract)		6-6		8-8		10-10

[4]	[8]	[6]	[12]	[8]	[16]	[10]	[20]

Bibliografie

en H. S. M. Coxeter, Regular Polytopes, Dover Publications, Inc., 1973, New York, p. 124.
en Coxeter, The Beauty of Geometry: Twelve Essays, Dover Publications, 1999, ISBN: 0-486-40919-8 (Chapter 5: Regular Skew Polyhedra in three and four dimensions and their topological analogues)
en Coxeter, H. S. M. Regular Skew Polyhedra in Three and Four Dimensions. Proc. London Math. Soc. 43, 33-62, 1937.
en Henry P. Manning, Munn & Company, The Fourth Dimension Simply Explained, 1910, New York. Available from the University of Virginia library. Also accessible online: The Fourth Dimension Simply Explained—contains a description of duoprisms (double prisms) and duocylinders (double cylinders). Googlebook
en John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss, The Symmetries of Things 2008, ISBN: 978-1-56881-220-5 (Chapter 26)
en Norman Johnson, The Theory of Uniform Polytopes and Honeycombs, Ph.D. Dissertation, University of Toronto, 1966

Portal matematică