Serie Fourier

De la Wikipedia, enciclopedia liberă

Seriile Fourier sunt o unealtă matematică folosită pentru a analiza funcţiile periodice descompunându-le într-o sumă ponderată de funcţii sinusoidale componente care sunt uneori denumite armonice Fourier normale, sau pe scurt armonice. Printre generalizări se numără seriile Fourier generalizate.

Seriile Fourier au multe utilizări practice, pentru că manipularea şi conceptualizarea coeficienţilor armonici sunt adesea mai uşoare decât lucrul cu funcţia originală. Domeniile de aplicabilitate includ ingineria electrică, analiza undelor, acustică, optică, prelucrarea semnalelor şi a imaginilor, şi compresia datelor. Folosind uneltele şi tehnicile spectroscopiei, de exemplu, astronomii pot deduce compoziţia chimică a unei stele prin analizarea componentelor armonice, sau spectrului, stelei care emite lumină. Analog, inginerii pot optimiza proiectarea unui sistem de telecomunicaţii cu ajutorul informaţiilor pe care le oferă componentele spectrale ale unui semnal de date pe care sistemul le transportă.

Seriile Fourier sunt numite după omul de ştiinţă şi matematicianul francez Joseph Fourier, care le-a folosit în importanta sa lucrare despre conducţia termică, Théorie Analytique de la Chaleur (Teoria analitică a căldurii), publicată în 1822.

[modifică] Definiţie

[modifică] Forma generală

Dată fiind o funcţie cu valori complexe f de argument real t, f: R → C, unde f(t) este continuă şi derivabilă pe porţiuni, periodică de perioadă T, şi integrabilă la pătrat pe intervalul de lungime T dintre $t 1$ şi $t 2$ , adică

$\int_{t_1}^{t_2} |f(t)|^2\, dt<+\infty$

unde

$T = t 2 - t 1$ este perioada,
$t 1$ and $t 2$ sunt limitele de integrare.

Dezvoltarea în serie Fourier a lui f este

$f(t) = \frac{1}{2} a_0 + \sum_{n=1}^{\infty}[a_n \cos(\omega_n t) + b_n \sin(\omega_n t)]$

unde, pentru orice întreg nenegativ n,

$\omega_n = n\frac{2\pi}{T}$ este armonica n (în radiani) a funcţiei f,
$a_n = \frac{2}{T}\int_{t_1}^{t_2} f(t) \cos(\omega_n t)\, dt$ sunt coeficienţii Fourier pari ai lui f, iar
$b_n = \frac{2}{T}\int_{t_1}^{t_2} f(t) \sin(\omega_n t)\, dt$ sunt coeficienţii Fourier impari ai lui f.

Echivalent, în formă cu exponenţiala complexă,

$f(t) = \sum_{n=-\infty}^{+\infty} c_n e^{i \omega_n t}$

unde:

$c_n = \frac{1}{T}\int_{t_1}^{t_2} f(t) e^{-i \omega_n t}\, dt$
$i$ este unitatea imaginară, şi
$e^{i \omega_n t} = \cos(\omega_n t) + i \sin(\omega_n t)$ conform cu formula lui Euler.

[modifică] Forma canonică

În cazul special unde perioada T = 2π, avem

$\omega_n = n \,$

În acest caz, dezvoltarea în serie Fourier se reduce la o formă deosebit de simplă:

$f(t) = \frac{1}{2} a_0 +\sum_{n=1}^{\infty}[a_n \cos(nt) + b_n \sin(nt)]$

unde

$a_n = \frac{1}{\pi}\int_{-\pi}^{\pi} f(t) \cos(nt)\, dt$
$b_n = \frac{1}{\pi}\int_{-\pi}^{\pi} f(t) \sin(nt)\, dt$

oricare ar fi un întreg nenegativ n.

sau, echivalent:

$f(t) = \sum_{n=-\infty}^{+\infty} c_n e^{i nt}$

unde

$c_n = \frac{1}{2 \pi}\int_{-\pi}^{\pi} f(t) e^{-i nt}\, dt = \frac{1}{2}(a_n-ib_n).$

[modifică] Alegerea formei

Forma pentru perioada T poate fi uşor derivată din cea canonică cu schimbarea de variabilă definită de $x=\frac{2\pi}{T}t$ . De aceea, ambele formulări sunt echivalente. Totuşi, forma pentru perioada T este preferată în majoritatea cazurilor practice pentru că este direct aplicabilă. Pentru teorie, este preferată forma canonică deoarece este mai elegantă şi mai uşor de interpretat matematic.

[modifică] Exemple

[modifică] Serii Fourier simple

Fie f periodică de perioadă $2π$ , cu $f (x) = x$ pentru x între −π şi π. Se observă că această funcţie este o versiune periodică a funcţiei identitate.

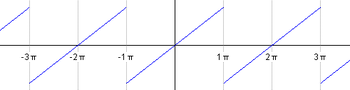
Graficul unei funcţii identitate periodice - o undă dinţi de fierăstrău.

Grafic animat cu primele cinci sume parţiale ale seriilor Fourier pentru funcţia identitate periodică

Se vor calcula coeficienţii Fourier pentr această funcţie.

$\begin{align} a_n &{}= \frac{1}{\pi}\int_{-\pi}^{\pi}f(x)\cos(nx)\,dx \\ &{}= \frac{1}{\pi}\int_{-\pi}^{\pi}x \cos(nx)\,dx \\ &{}= 0. \end{align}$

$\begin{align} b_n &{}= \frac{1}{\pi}\int_{-\pi}^{\pi}f(x)\sin(nx)\,dx \\ &{}= \frac{1}{\pi}\int_{-\pi}^{\pi} x \sin(nx)\, dx \\ &{}= \frac{2}{\pi}\int_{0}^{\pi} x\sin(nx)\, dx \\ &{}= \frac{2}{\pi} \left(\left[-\frac{x\cos(nx)}{n}\right]_0^{\pi} + \left[\frac{\sin(nx)}{n^2}\right]_0^{\pi}\right) \\ &{}= 2\frac{(-1)^{n+1}}{n}.\end{align}$

Se observă că a_n sunt 0 deoarece $x\mapsto x\cos(nx)$ sunt funcţii pare. Deci seria Fourier pentru această funcţie este:

$f(x)=\frac{a_0}{2} + \sum_{n=1}^{\infty}\left[a_n\cos\left(nx\right)+b_n\sin\left(nx\right)\right]$

$=2\sum_{n=1}^{\infty}\frac{(-1)^{n+1}}{n} \sin(nx), \quad \forall x\in [-\pi,\pi].$

O aplicaţie a acestei serii Fourier este calculul funcţiei Riemann zeta la s = 2; Conform teoremei lui Parseval, avem:

$\frac{1}{2\pi} \int_{-\pi}^\pi x^2 dx=\frac{1}{2}\sum_{n>0}\left[2\frac{(-1)^n}{n}\right]^2$

de unde rezultă: $\sum_{n>0}\frac{1}{n^2}=\frac{\pi^2}{6}$ .

[modifică] Ecuaţia undei

Ecuaţia undei descrie mişcarea unei coarde vibrante, care poate fi ţinuta fixă de capete. Soluţia acestei probleme necesită dezvoltarea în serie trigonometrică a unei funcţii generale f care dispare la capetele unui interval de la x=0 la x=L. Seria Fourier pentru o asemenea funcţie ia forma

$f(x) = \sum_{n=1}^{\infty} b_n \sin \left( \frac{n\pi}{L} x \right)$

unde

$b_n = \frac{2}{L} \int_0^L f(x) \sin \left( \frac{n\pi}{L} x\right)\, dx.$

Vibraţiile aerului într-o ţeavă deschisă la un capăt şi închisă la celălalt sunt şi ele descrise de ecuaţia undei. Soluţia ei este dată de dezvoltarea în serie Fourier a unei funcţii care dispare la x = 0 şi care nu mai este derivabilă la x=L. Seria sa Fourier ia forma

$f(x) = \sum_{n=1}^{\infty} b_n \sin \left( \frac{(2n +1)\pi}{2L} x \right)$

unde

$b_n = \frac{2}{L} \int_0^L f(x) \sin \left( \frac{(2n+1)\pi}{2L} x\right)\, dx.$

[modifică] Interpretare: descompunerea unei mişcări în rotaţii

Seriile Fourier au o interpretare cinematică. Funcţia $t\mapsto f(t)$ poate fi văzută ca mişcare a unui obiect într-un plan (t reprezentând timpul). Deoarece f ia valori complexe, se poate scrie

$f(t)=u(t)+i v(t). \,$

pentru funcţii cu valori reale u şi v. În această formă, putem interpreta f ca sumă de translaţii orizontale şi verticale.

De la un moment $t$ la un moment $t + d t$ , unde dt e o perioadă incrementală mică, obiectul se mişcă de la punctul $A=\left[\begin{matrix}u(t)\\v(t)\end{matrix}\right]$ la punctul $B=\left[\begin{matrix}u(t+dt)\\v(t+dt)\end{matrix}\right]$ , care corespunde unei translaţii infinitezimale în spaţiu după vectorul $\overrightarrow{AB}=\left[\begin{matrix}u(t+dt)-u(t)\\v(t+dt)-v(t)\end{matrix}\right]$ . Rezultă că f se poate scrie de forma:

$f(t)=\left[\begin{matrix}u(dt)-u(0)\\v(dt)-v(0)\end{matrix}\right]+\left[\begin{matrix}u(2dt)-u(dt)\\v(2dt)-v(dt)\end{matrix}\right]+\cdots+\left[\begin{matrix}u(t+dt)-u(t)\\v(t+dt)-v(t)\end{matrix}\right]$

$=\int_0^t\frac{1}{dx}\left[\begin{matrix}u(x+dx)-u(x)\\v(x+dx)-v(x)\end{matrix}\right]\,dx.$

În loc de a vedea pe f ca pe o sumă de translaţii infinitezimale, o putem vedea ca pe o sumă infinită de rotaţii cu diferite raze. Această interpretare este convenabilă, mai ales când mişcarea este periodică.

Fie $χ n = e i n x$ rotaţia de n-ture pe secundă, de rază 1). Se doreşte scrierea f ca $f(x)=\sum c_n \chi_n$ . Se poate demonstra că razele de rotaţie (coeficienţii $c n$ ) sunt exact cei daţi în paragraful anterior.

De exemplu, graficul funcţiei $f:t\mapsto 2\cos\left(\frac{t}{2}\right)e^{\frac{3}{2}it}$ este închis, ceea ce înseamnă că funcţia este periodică. Bucla de pe curbă sugerează că este suma a două funcţii periodice, una cu o perioadă mai scurtă decât cealaltă. Într-adevăr, sepoate scrie: $f (t) = e i t + e 2 i t = χ 1 (t) + χ 2 (t)$ . Toţi coeficienţii săi Fourier sunt zero cu excepţia $c 1 = 1$ şi $c 2 = 1$ . Interpretarea grafică a unei rotaţii este mult mai dificil de realizat decât a translaţiilor, pentru că în loc de a imagina vizual mişcarea dintr-u punct în altul, trebuie adăugată toată mişcarea pentru a avea sens descompunerea (gândirea se face în termeni de frecvenţă de rotaţie şi nu de timp).

Matematic, adoptarea acestui punct de vedere reprezintă o folosire a seriilor Fourier ca pe o unealtă de înţelegere a operatorilor liniari care comută cu translaţia. Funcţiile $χ n$ sunt exact caracterele multiplicative ale grupului $\mathbb{R}/2\pi\mathbb{Z}$ .

[modifică] Istoric

[modifică] Context

Seriile Fourier au fost denumite în onoarea lui Joseph Fourier (1768-1830), care a avut importante contribuţii la studiul seriilor trigonometrice, după investigaţii preliminare ale lui Madhava, Nilakantha Somayaji, Jyesthadeva, Leonhard Euler, Jean le Rond d'Alembert şi Daniel Bernoulli. El a aplicat această tehnică pentru a găsi soluţia pentru ecuaţia căldurii, publicându-şi rezultatele iniţiale în 1807 şi 1811, şi publicând lucrarea Théorie analytique de la chaleur în 1822.

Dintr-un punct de vedere modern, rezultatele lui Fourier sunt puţin informale, datorită unei lipse de notaţie precisă a funcţiei şi integralei la începutul secolului al XIX-lea (de exemplu, la acea vreme nu era lămurit dacă o funcţie definită pe două intervale diferite cu două expresii diferite mai era tot o singură funcţie). Mai târziu, Dirichlet şi Riemann au exprimat rezultatele lui Fourier cu mai mare precizie şi rigurozitate.

[modifică] Un articol revoluţionar

În lucrarea lui Fourier intitulată Mémoire sur la propagation de la chaleur dans les corps solides, la paginile 218 şi 219, se pot citi următoarele:

$\varphi(y)=a\cos\frac{\pi y}{2}+a'\cos 3\frac{\pi y}{2}+a''\cos5\frac{\pi y}{2}+\cdots.$

Înmulţind ambele părţi cu $\cos(2i+1)\frac{\pi y}{2}$ , şi apoi integrând de la $y = - 1$ la $y = + 1$ rezultă:

$a_i=\int_{-1}^1\varphi(y)\cos(2i+1)\frac{\pi y}{2}\,dy.$

În aceste câteva rânduri, surprinzător de apropiate de formalismul modern folosit în seriile Fourier, Fourier a revoluţionat fără să vrea atât matematica cât şi fizica. Deşi serii trigonometrice similare mai fuseseră folosite anterior de Euler, d'Alembert, Daniel Bernoulli şi Gauss, Fourier a fost primul care a recunoscut că astfel de serii trigonometrice pot reprezenta funcţii arbitrare, chiar şi funcţii cu discontinuităţi. A trebuit să treacă mulţi ani pentru a clarifica această idee, care a condus la importante teorii asupra convergenţei, spaţiilor de funcţii, şi analizei armonice.

Lucrarea lui Fourier a fost atât de originală încât, când a trimis-o în 1807, comisia (compusă din alţi mari matematicieni ca Lagrange, Laplace, Malus şi Legendre, printre alţii) a concluzionat: ...maniera în care autorul ajunge la aceste ecuaţii nu este una scutită de dificultăţi şi analiza sa încă lasă de dorit la capitolele generalitate şi chiar rigoare.

[modifică] Naşterea analizei armonice

Din vremea lui Fourier până astăzi au fost descoperite multe alte abordări ale definirii şi înţelegerii conceptului de serie Fourier, toate fiind corecte şi echivalente matematic, dar fiecare punând accent pe alte aspecte ale subiectului. Unele dintre cele mai elegante şi mai puternice abordări sunt bazate pe idei şi unelte matematice care nu erau disponibile la momentul când Fourier şi-a terminat lucrarea. Fourier a definit iniţial seriile Fourier pentru funcţii reale de argument real, şi folosindu-se de funcţiile sinus şi cosinus ca bază a descompunerii.

Multe alte transformări de tip Fourier au mai fost definite, extinzând cu alte noi aplicaţii ideea iniţială de reprezentare a oricărei funcţii periodice ca suprapunere de armonice. Această arie generală de studiu este uneori numită analiză armonică.

[modifică] Derivări moderne ale coeficienţilor Fourier

Metoda lui Fourier de calcul al coeficienţilor seriei este foarte practică şi potrivită problemei pe care o tratează (propagarea căldurii). Totuşi, această metodă a fost generalizată între timp la o clasă mult mai largă de probleme: scrierea unei funcţii ca sumă de funcţii periodice.

Mai exact, dacă f:R → C este o funcţie, am vrea să scriem această funcţie ca sumă de funcţii trigonometrice, i.e. $f(x)=\sum c_n e^{inx}$ . Variantele de alegere a funcţiilor trebuie să fie restrânse pentru ca descompunerea să aibă sens. În primul rând, dacă f este de perioadă T, atunci prin schimbarea variabilelor, se poate studia $x\mapsto f\left(\frac{T}{2\pi}x\right)$ de perioadă 2π. Aceasta simplifică mult notaţia şi permite utilizarea unei forme standard (canonice). Putem restrânge astfel studiul funcţiilor $x\mapsto f\left(\frac{T}{2\pi}x\right)$ la orice interval de lungime 2π, cum ar fi [-π,π].

Luând funcţia f:R → C din mulţimea celor continue pe porţiuni, funcţii periodice de perioadă 2π cu $\int_{-\pi}^\pi |f(x)|^2 \, dx<+\infty$ . De fapt, se iau funcţii din spaţiul Lp L²(μ), unde μ este măsura Lebesgue normalizată a intervalului [-π,π] (astfel încât $\int_{[-\pi,\pi]}f \, d\mu=\frac{1}{2\pi}\int_{-\pi}^\pi f(x)\,dx$ .

[modifică] Coeficienţi Fourier complecşi

Putem transforma L²(μ) într-un spaţiu Hilbert, ceea ce este potrivit pentru proiecţii ortogonale, prin definirea produsului scalar:

$\langle f, g \rangle = \int_{[-\pi,\pi]} f \overline{g} \,d\mu=\frac{1}{2\pi}\int_{-\pi}^\pi f(x)\overline{g(x)}\,dx,$

unde $\overline{f(x)}$ reprezintă conjugata lui f(x). Vom nota cu $\| \cdot \|$ norma asociată.

$E=\{t\mapsto e^{i n t},n\in\mathbb{Z}\}$ este o bază ortonormală din L²(μ), deci se poate scrie

$f(x)=\sum_{n\in\mathbb{Z}}\left\langle f,e^{i n x}\right\rangle e^{i n x}.$

De regulă se defineşte $\forall n\in\mathbb{Z}, c_n=\left\langle f,e^{i n x}\right\rangle$ . Aceste numere se numesc coeficienţi Fourier complecşi. Expresia lor este

$c_n = \frac{1}{2\pi} \int_{-\pi}^{\pi} f(x) e^{-i n x}\,dx.\,$

O formulare echivalentă este scrierea f ca sumă de funcţii sinus şi cosinus.

[modifică] Coeficienţi Fourier reali

Suma din secţiunea anterioară este simetrică în raport cu 0: într-adevăr, cu excepţia lui n = 0, un coeficient c_−n corespunde fiecărui coeficientc_n. Astfel ne amintim de formulele

$\cos x =\frac{e^{ix}+e^{-ix}}{2}{\rm~~~~and~~~~}\sin x =\frac{e^{ix}-e^{-ix}}{2i}.$

Astfel se pot exprima serii Fourier cu funcţii cu valori reale. Pentru a face aceasta se observă că

$f(x)=\sum_{n\in\mathbb{Z}}c_n e^{i n x}=c_0+\sum_{n>0}\left[c_{-n}e^{-i n x}+c_n e^{i n x}\right].$

După înlocuirea lui c_n cu expresia sa şi simplificarea rezultatului, obţinem

$f(x)=c_0+\sum_{n>0}\left[\frac{1}{\pi}\left(\int_{-\pi}^\pi f(t)\cos\left(n t\right)\, dt\right)\cos\left(n x\right)+\frac{1}{\pi}\left(\int_{-\pi}^\pi f(t)\sin\left(n t\right)\, dt\right)\sin\left(n x\right)\right].$

Dacă pentru un număr întreg nenegativ n, definim coeficienţii Fourier reali a_n şi b_n prin

$a_n = \frac{1}{\pi}\int_{-\pi}^{\pi} f(x) \cos\left(n x\right)\, dx,$

$b_n = \frac{1}{\pi}\int_{-\pi}^{\pi} f(x) \sin\left(n x\right)\, dx,$

obţinem:

$f(x)=\frac{a_0}{2}+\sum_{n>0}\left[a_n\cos\left(n x\right)+b_n\sin\left(n x\right)\right].$

[modifică] Proprietăţi

Următoarele proprietăţi se deduc din formula lui Euler: $e^{ix} = \cos x + i\sin x. \!$

a n = c n + c - n

şi $b_n=i(c_n-c_{-n})\mbox{ for all } n \mbox{ and }\,$

$c_n=\frac{a_n-ib_n}{2}$ şi $c_{-n}=\frac{a_n+ib_n}{2}\mbox{ for all } n.$

Dacă f este o funcţie impară, atunci $a n = 0$ oricare ar fi $n$ pentru că $f(x)\cos\left(n\pi\frac{x}{T}\right)$ este tot pară, deci integrala sa pe intervalul $[ - T, T]$ este zero. Dacă f este o funcţie pară, atunci $b n = 0$ dintr-un motiv similar.

Dacă f este continuă pe porţiuni, $\lim_{n\rightarrow +\infty}c_n(f)=0$ , $\lim_{n\rightarrow +\infty}c_{-n}(f)=0$ , $\lim_{n\rightarrow +\infty}a_n(f)=0$ şi $\lim_{n\rightarrow +\infty}b_n(f)=0.$

Dacă f este continuu diferenţiabilă de k ori pe porţiuni, atunci se pot calcula uşor coeficienţii Fourier ai lui $f (k)$ din cei ai lui f:

$c_n\left(f^{(k)}\right)=(in)^k c_n(f),$

unde $f (k)$ este derivata de ordin k a lui f.

Oricare ar fi un întreg pozitiv al lui k, dacă f este C^k − 1 şi C^k pe porţiuni, atunci

$\lim_{n\rightarrow +\infty}|n^kc_n(f)|=0$ pentru că $n^kc_n(f)=i^{-k}c_n\left(f^{(k)}\right)\rightarrow 0.$

Aceasta înseamnă că seria $c n (f)$ este rapid descrescătoare.

[modifică] Cazul general

Seriile Fourier exploatează periodicitatea funcţiei f dar dacă f este periodică în mai multe variabile, sau chiar f neperiodică? Aceste probleme i-au condus pe matematicieni şi pe fizicienii teoreticieni să încerce să definească seriile Fourier pe orice grup G. Avantajul este, de exemplu, definirea seriilor Fourier pentru funcţii de mai multe variabile. Seriile Fourier şi transformata Fourier folosite în prelucrarea semnalelor devin astfel cazuri speciale ale acestei teorii şi sunt mai uşor de interpretat.

Dacă G grup Abelian local compact şi T este cercul unitate, se poate defini dualul lui G prin $\widehat{G} = \{\chi:G\rightarrow\mathbb{T} \mbox{ omomorfism}\}$ . Acestea constituie mulţimea rotaţiilor pe cercul unitate şi elementele sale se numesc caractere. Se poate defini un produs scalar $\langle\cdot,\cdot\rangle$ pe C[G] prin: $\langle\chi_1, \chi_2\rangle=\int_{G}\chi_1(g) \overline{\chi_2(g)}\,dg$ . $\widehat{G}$ este atunci bază ortonormală în C[G] în raport cu acest produs scalar. Fie f :G → C. Coeficienţii Fourier ai lui f sunt definiţi prin: $\widehat{f}(\chi)=\langle f,\chi\rangle$ şi avem $f(g) = \int_{\widehat{G}} \widehat{f} (\chi)\chi(g)\,d\chi$ . Dacă grupul este discret, atunci integrala se reduce la o sumă.

De exemplu, coeficienţii Fourier ai acestui articol sunt obţinuţi luând G = R/2πZ. Obţinem

$\widehat{G}=\{\chi_n:t\mapsto e^{i n t}, n\in\mathbb{Z}\}$

şi

$c_n(f) = \widehat{f}(\chi_n) = \int_G f(g)\overline{\chi(g)}\,dg = \frac{1}{2 \pi}\int_{-\pi}^{\pi} f(t) e^{-i nt}\,dt.$

Funcţiile periodice în n dimensiuni pot fi definite pe un tor n-dimensional (funcţia ia valoare pe fiecare punct de pe tor). Un astfel de tor este definit prin Tⁿ = Rⁿ/(2πZ)ⁿ. Pentru n = 1 torul este un cerc, pentru n = 2 este produsul cartezian a două cercuri, adică un tor obişnuit. Alegând G = Tⁿ rezultă seria Fourier corespunzătoare.

[modifică] Aproximarea şi convergenţa seriilor Fourier

[modifică] Definiţia unei serii Fourier

Fie $\chi_n(x)=e^{in\pi \frac{x}{T}}$ . Se numeşte serie Fourier a funcţiei f seria $\sum c_n \chi_n$ . Pentru orice întreg pozitiv N, $f_N(x)=\sum_{n=-N}^Nc_n \chi_n(x)$ se numeşte a N-a sumă parţială a seriei Fourier a acestei funcţii.

[modifică] Aproximarea cu sume parţiale

Să zicem că dorim să găsim cea mai bună aproximare a lui f folosind doar funcţiile $χ n$ pentru n de la $- N$ la N. Fie $\mathcal{T}_N=\left\{p=\sum_{n=-N}^N x_n \chi_n, x_n\in\mathbb{C}\right\}$ . Încercăm sa găsim coeficienţii $(x_{-N},\dots,x_{N})$ astfel încât $\|f-p\|$ este minim (unde $\| \cdot \|$ este norma).

Avem $\|f-p\|^2=\|f\|^2-2\mbox{Re}\langle f,p\rangle+\|p\|^2$ , unde Re(z) notează partea reală a lui z.

$\langle f,p\rangle=\sum_{n=-N}^N\overline{x_n}\langle f,\chi_n\rangle.$

Teorema lui Parseval (ce poate fi dedusă independent din seriile Fourier) dă

$\|p\|^2=\sum_{n=-N}^N|x_n|^2.$

Prin definiţie, $c_n=\langle f,\chi_n\rangle$ ; deci

$\|f-p\|^2=\|f\|^2+\sum_{n=-N}^N\left[|c_n-x_n|^2-|c_n|^2\right].$

Este clar că această expresie este minimă pentru $x n = c n$ şi doar pentru această valoare.

Deci există un singur $f_N\in\mathcal{T}_N$ astfel încât

$\|f-f_N\|=\min_{p\in\mathcal{T}_N}\left\{\|f-p\|,p\in\mathcal{T}_N\right\},$

este dat de

$f_N(x)=\sum_{n=-N}^N c_n \chi_n(x),$

unde

$c_n=\frac{1}{2T}\int_{-T}^T f(t)\chi_{-n}(t)\,dt.$

Deci cea mai bună aproximare a lui f ce poate fi făcută folosind doar funcţiile $\chi_n(x)=e^{in\pi \frac{x}{T}}$ pentru n de la $- N$ la N este exact a N-a sumă parţială a seriei Fourier.

[modifică] Convergenţa

În timp ce coeficienţii Fourier a_n şi b_n pot fi definiţi formal pentru orice funcţie integrabilă, dacă această funcţie converge sau nu la f(x) depinde de proprietăţile lui f.

Cel mai simplu răspuns este că pentru ca seria să conveargă, f trebuie să fie integrabilă la pătrat, deci

$\lim_{N\rightarrow\infty}\int_{-\pi}^\pi\left|f(x)-\sum_{n=-N}^{N} c_n\,\chi_n(x)\right|^2\,dx=0.$

Aceasta este convergenţă în norma dată de spaţiul L². Demonstraţia acestui rezultat este simplă, spre deosebire de rezultatul mult mai puternic dat de Lennart Carleson conform căruia seriile converg aproape în orice caz.

Există mai multe teste care asigură că seria converge într-un punct dat, de exemplu, dacă funcţia este diferenţiabilă în x. Nici chiar o mică discontinuitate a derivatei nu constituie o problemă: dacă funcţia are derivată la stânga şi la dreapta în x, atunci seria Fourier va converge la media limitelor la stânga şi la dreapta (dar vezi Fenomenul Gibbs). Totuşi, fapt considerat de mulţi surprinzător, seria Fourier a unei funcţii continue nu trebuie neapărat să fie convergentă în fiecare punct.

Această situaţie neplăcută este echilibrată de o teoremă a lui Dirichlet care afirmă că dacă f este periodică de perioadă $2 T$ şi derivată cu derivata continuă, atunci seria ei Fourier converge în fiecare punct şi $\sum_{n\in\mathbb{Z}} c_n \chi_n(x)=\frac{f(x^+)+f(x^-)}{2}$ , unde $f(x^+)=\lim_{t\rightarrow x, t>x} f(x)$ şi $f(x^-)=\lim_{t\rightarrow x, t<x} f(x)$ . Dacă f este continuă şi cu derivata continuă pe porţiuni, atunci seria Fourier converge uniform.

În 1922, Andrei Kolmogorov a publicat un articol intitulat Une série de Fourier-Lebesgue divergente presque partout în care a dat un exemplu de funcţie integrabilă Lebesgue a cărei serie Fourier divere aproape în fiecare punct. Această funcţie nu este din $L 2 (μ)$ .

[modifică] Teoremele lui Plancherel şi Parseval

O altă proprietate importantă a seriilor Fourier este Teorema lui Plancherel. Fie $f,g\in L^2(\mu)$ şi $c n (f), c n (g)$ coeficienţii Fourier complecşi corespunzători. Atunci

$\sum_{n\in\mathbb{Z}} c_n(f)\overline{c_n(g)} = \frac{1}{2T} \int_{-T}^T f(x)\overline{g(x)}\,dx$

unde cu $\overline{z}$ s-a notat conjugatul lui z.

Teorema lui Parseval, un caz special al teoremei lui Plancherel, afirmă că:

$\sum_{n\in\mathbb{Z}} |c_n(f)|^2 = \frac{1}{2T} \int_{-T}^T |f(x)|^2 \,dx$

reformulabilă astfel pentru coeficienţi Fourier reali:

$\frac{a_0^2}{4} + \frac{1}{2} \sum_{n=1}^\infty \left( a_n^2 + b_n^2 \right) = \frac{1}{2T} \int_{-T}^T |f(x)|^2\, dx.$

Aceste teoreme se pot demonstra folosind relaţiile de ortogonalitate. Ele pot fi interpretate fizic spunând că scrierea unui semnal ca serie Fourier series nu îi modifică energia.

[modifică] Bibliografie

Joseph Fourier, tradusă în engleză de Alexander Freeman (publicată în 1822, tradusă 1878, republicată 2003). The Analytical Theory of Heat. Dover Publications. ISBN 0-486-49531-0. republicarea completă din 2003 a traducerii în engleză din 1878 de Alexander Freeman a lucrării lui Fourier Théorie Analytique de la Chaleur, iniţial publicată în 1822.
Yitzhak Katznelson, An introduction to harmonic analysis, Second corrected edition. Dover Publications, Inc., New York, 1976. ISBN 0-486-63331-4
Felix Klein, Development of mathematics in the 19th century. Mathsci Press Brookline, Mass, 1979. Translated by M. Ackerman from Vorlesungen über die Entwicklung der Mathematik im 19 Jahrhundert, Springer, Berlin, 1928.
Walter Rudin, Principles of mathematical analysis, Third edition. McGraw-Hill, Inc., New York, 1976. ISBN 0-07-054235-X
William E. Boyce and Richard C. DiPrima, Elementary Differential Equations and Boundary Value Problems, Eighth edition. John Wiley & Sons, Inc., New Jersey, 2005. ISBN 0-471-43338-1

Serie Fourier

De la Wikipedia, enciclopedia liberă

Cuprins

[modifică] Definiţie

[modifică] Forma generală

[modifică] Forma canonică

[modifică] Alegerea formei

[modifică] Exemple

[modifică] Serii Fourier simple

[modifică] Ecuaţia undei

[modifică] Interpretare: descompunerea unei mişcări în rotaţii

[modifică] Istoric

[modifică] Context

[modifică] Un articol revoluţionar

[modifică] Naşterea analizei armonice

[modifică] Derivări moderne ale coeficienţilor Fourier

[modifică] Coeficienţi Fourier complecşi

[modifică] Coeficienţi Fourier reali

[modifică] Proprietăţi

[modifică] Cazul general

[modifică] Aproximarea şi convergenţa seriilor Fourier

[modifică] Definiţia unei serii Fourier

[modifică] Aproximarea cu sume parţiale

[modifică] Convergenţa

[modifică] Teoremele lui Plancherel şi Parseval

[modifică] Bibliografie

Vizualizări

Unelte personale

Navigare

participare

Căutare

Trusa de unelte

În alte limbi