Hiperbolă unitate

Hiperbola unitate este cu albastru, conjugata sa este cu verde, iar asimptotele sunt cu roșu

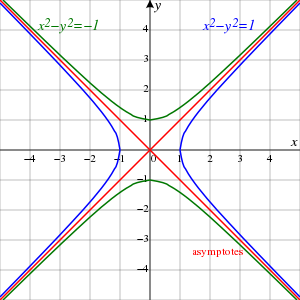
în geometrie hiperbola unitate este mulțimea punctelor (x,y) din planul cartezian care satisfac ecuația implicită^⁠(d) $x^{2}-y^{2}=1.$ În studiul grupurilor ortogonale nedefinite^⁠(d) hiperbola unitate constituie baza pentru o lungime radială alternativă

$r={\sqrt {x^{2}-y^{2}}}.$

În timp ce cercul unitate își înconjoară centrul, hiperbola unitate necesită hiperbola conjugată $y^{2}-x^{2}=1$ pentru a o completa în plan. Această pereche de hiperbole au în comun asimptotele y = x și y = −x. Împreună cu conjugata hiperbolei unitate, lungimea radială alternativă este $r={\sqrt {y^{2}-x^{2}}}.$

Hiperbola unitate este un caz particular al hiperbolei echilaterale, cu o anumită orientare, poziționare și scară. Ca atare, excentricitatea sa este ${\sqrt {2}}.$

Hiperbola unitate are aplicații în geometria analitică, în cazuri în care cercul trebuie înlocuit cu hiperbola. Un exemplu important este reprezentarea spațiu-timpului ca un spațiu pseudoeuclidian^⁠(d). Acolo asimptotele hiperbolei unitate formează un con de lumină^⁠(d). Mai mult, atenția lui Gregoire de Saint-Vincent asupra zonelor din sectorul hiperbolic a dus la funcția logaritmului și la parametrizarea modernă a hiperbolei prin sectoare. Când au fost înțelese noțiunile de hiperbolă conjugată și unghi hiperbolic^⁠(d) clasicele numere complexe, care sunt construite pe baza cercului unitate, pot fi înlocuite cu numere construite pe baza hiperbolei unitate (numerele complexe hiperbolice^⁠(d)).

Asimptote

Articol principal: Asimptotă.

În general, se spune că asimptotele unei curbe converg spre curbă. În geometria algebrică și teoria curbelor algebrice^⁠(d) există o abordare diferită a asimptotelor. Curba este mai întâi interpretată în planul proiectiv^⁠(d) folosind coordonate omogene. Apoi asimptotele sunt drepte care sunt tangente curbei proiective în punctul de la infinit, eludând astfel orice nevoie de un concept de distanță și convergență. Într-un cadru comun ( x, y, z ) sunt coordonate omogene cu dreapta de la infinit determinate de ecuația z = 0. De exemplu, C. G. Gibson a scris:

Pentru hiperbola echilaterală standard $f=x^{2}-y^{2}-1$ din ℝ², curba proiectivă corespondentă este $F=x^{2}-y^{2}-z^{2},$ care intersectează z = 0 în punctele P = (1 : 1 : 0) și Q = (1 : −1 : 0). Ambele puncte P și Q sunt intersecții simple cu F, cu tangentele x + y = 0, x − y = 0; obținându-se astfel „asimptotele” familiare din geometria elementară.

Parametrizare

Ramurile hiperbolei unitate sunt punctele $(\cosh a,\sinh a)$ și $(-\cosh a,-\sinh a)$ în funcție de parametrul $a$ al unghiului hiperbolic

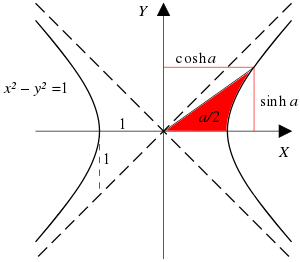
O modalitate directă de parametrizare a hiperbolei unitate începe cu hiperbola xy = 1 parametrizată cu funcția exponențială: $(e^{t},\ e^{-t}).$

Această hiperbolă este transformată în hiperbolă unitate printr-o transformare liniară având matricea $A={\tfrac {1}{2}}{\begin{pmatrix}1&1\\1&-1\end{pmatrix}}\ :$

$(e^{t},\ e^{-t})\ A=({\frac {e^{t}+e^{-t}}{2}},\ {\frac {e^{t}-e^{-t}}{2}})=(\cosh t,\ \sinh t).$

Parametrul t este unghiul hiperbolic, care este argumentul funcțiilor hiperbolice.

Ca o anumită conică, hiperbola poate fi parametrizată prin procesul de adăugare a punctelor pe o conică. Următoarea descriere a fost dată de analiștii ruși:

Se pune un punct E pe conică. Se consideră punctele în care dreapta trasată prin E paralel cu AB intersectează conica a doua oară ca fiind suma punctelor A și B.

Pentru hiperbola $x^{2}-y^{2}=1$ cu punctul E = (1,0) suma punctelor $(x_{1},\ y_{1})$ și $(x_{2},\ y_{2})$ este punctul $(x_{1}x_{2}+y_{1}y_{2},\ y_{1}x_{2}+y_{2}x_{1})$ cu parametrizarea $x=\cosh \ t$ și $y=\sinh \ t$, această adăugare corespunde adăugării parametrului t.

Bibliografie

• en F. Reese Harvey (1990) Spinors and calibrations, Figure 4.33, page 70, Academic Press, ISBN: 0-12-329650-1 .