Primitivă
În analiza matematică, o primitivă sau integrală nedefinită[a] a unei funcții f este o funcție F a cărei derivată este egală cu f, adică, F ′ = f. Procesul de calcul al primitivelor se numește primitivare (sau integrare nedefinită). Primitivele sunt legate de integralele definite prin teorema fundamentală a calculului integral, și furnizează un mijloc convenabil de calcul al integralelor definite ale multor funcții.
Exemplu[modificare | modificare sursă]
Funcția F(x) = x3/3 este o primitivă pentru f(x) = x2. Întrucât derivata unei constante este zero, x2 va avea un număr infinit de primitive; astfel (x3/3) + 0, (x3 / 3) + 7, (x3 / 3) − 42, etc. Astfel, întreaga familie de primitive ale lui x2 se poate obține prin modificarea valorii lui C în F(x) = (x3 / 3) + C; unde C este o constantă arbitrară cunoscută drept constantă de integrare. Esențial este că graficul fiecărei primitive a unei funcții date este o translație pe verticală ale unei alte funcții din familie, locația fiecărei primitive fiind dată de valoare a lui C.
Utilizări și proprietăți[modificare | modificare sursă]
Primitivele sunt importante deoarece pot fi utilizate la calculul integralelor definite, folosind teorema fundamentală a calculului integral: dacă F este o primitivă a unei funcții integrabile f, atunci:
Din acest motiv, una din infinit de multele primitive ale unei funcții date f este uneori numită "integrală generală" sau "integrală nedefinită" a lui f și este scrisă folosind simbolul de integrală fără limite:
Dacă F este o primitivă a lui f, și f este definită pe un interval, orice altă primitvă G a lui f diferă de F printr-o constantă: există un număr C astfel încât G(x) = F(x) + C oricare ar fi x. C este numită constantă de integrare. Dacă domeniul lui F este o reuniune de două sau mai multe intervale disjuncte, atunci se pot alege constante de integrare diferite pentru fiecare interval. De exemplu
este primitiva cea mai generală pentru pe domeniul său general
Toate funcțiile continue f admit primitive, iar o primitivă F este dată de integrala definită f cu limita de sus variabilă:
Varierea limitei de jos produce alte primitive (dar nu neapărat pe toate). Aceasta este o altă formulare a teoremei fundamentale a calculului integral.
Există multe funcții ale căror primitive, deși există, nu pot fi exprimate în termeni de funcții elementare [b]. Astfel de exemple sunt
Tehnici de integrare[modificare | modificare sursă]
Calculul primitivelor funcțiilor elementare este adesea considerat mai dificil decât găsirea derivatelor acestora. Pentru unele funcții elementare, este imposibil să se exprime primitivele în termeni de alte funcții elementare.
Avem la dispoziție mai multe metode:
- liniaritatea integrării ne permite să descompunem integrale mai complexe în altele mai simple
- integrarea prin substituție, adesea combinată cu identitățile trigonometrice sau cu logaritmul natural
- integrarea prin părți pentru integrarea produsului de funcții
- metoda fracțiilor parțiale permite integrarea tuturor funcțiilor raționale (fracții de două polinoame)
- algoritmul Risch
- integralele pot fi căutate într-un tabel de integrale
- la integrarea multiplă, se pot folosi și alte tehnici adiționale, vezi de exemplu integralele duble și coordonatele polare, Jacobianul și teorema lui Stokes
- Sistemele algebrice pe calculator se pot folosi pentru a automatiza parțial sau total munca depusă în tehnicile simbolice de mai sus, ceea ce e deosebit de util când manipulările algebrice implicate sunt foarte complexe sau laborioase
- dacă o funcție nu are primitive elementare (de exemplu, exp(x2)), integralele sale definite pot fi aproximate folosind integrarea numerică
Primitivele funcțiilor discontinue[modificare | modificare sursă]
Pentru a ilustra unele din subtilitățile teoremei fundamentale, se poate observa ce fel de funcții discontinue admit primitive. Chiar dacă sunt încă întrebări fără răspuns în această zonă, se știe că:
- Unele funcții patologice cu mulțimi mari de discontinuități ar putea admite totuși primitive.
- În unele cazuri, primitivele unor astfel de funcții pot fi găsite prin integrare Riemann, pe când în alte cazuri astfel de funcții nu sunt integrabile Riemann.
Să presupunem că funcțiile despre care vorbim sunt definite pe intervale deschise.
- O condiție necesară, dar nu suficientă, pentru ca o funcție f să admită primitivă este ca f să aibă proprietatea Darboux. Adică, dacă [a,b] este un subinterval al domeniului de definiție al lui f și d este un număr real între f(a) și f(b), atunci există un c între a și b astfel încât f(c)=d. Pentru a vedea aceasta, fie F o primitivă a lui f și să considerăm funcția continuă g(x)=F(x)-dx pe intervalul închis [a, b]. Atunci g trebuie să aibă fie un minim, fie un maxim c în intervalul deschis (a,b) și astfel 0=g′(c)=f(c)-d.
- Mulțimea discontinuităților lui f trebuie să fie o mulțime neglijabilă. Această mulțime trebuie să fie și mulțime F-sigma (pentru că mulțimea discontinuităților unei funcții trebuie să fie de acest fel). Mai mult, pentru orice mulțime F-sigma neglijabilă, se poate construi o funcție f care are o primitivă, și care are mulțimea dată ca mulțime de discontinuități.
- Dacă f admite primitive, este mărginită pe subintervale închise finite ale domeniului de definiție și are o mulțime de discontinuități de măsură Lebesgue 0, atunci se poate găsi o primitivă prin integrare.
- Dacă f admite o primitivă F pe un interval închis [a,b], atunci oricum s-ar alege o partiție , dacă se aleg puncte așa cum este specificat în Teorema de medie, atunci suma Riemann corespunzătoare tinde la valoarea F(b)-F(a).
- Totuși dacă mulțimea discontinuităților lui f are măsura Lebesgue pozitivă, la o altă alegere a punctelor intermediare se obține o valoare semnificativ diferită de suma Riemann, indiferent cât de fină este partiția. Vezi exemplul 4 de mai jos.
Exemple[modificare | modificare sursă]
- Funcția
- Funcția
- Dacă f(x) este funcția din exemplul 1 și F este o primitivă a ei, și este o mulțime densă numărabilă a intervalului deschis , atunci funcția
- Fie o submulțime densă numărabilă a intervalului deschis . Considerăm funcția strict crescătoare și continuă

Figura 1. 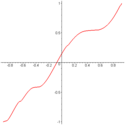
Figura 2. pentru toate valorile x unde seria este convergentă, și și că graficul F(x) are tangentă verticală în toate celelalte valori ale lui x. În particular graficul are tangente verticale în toate punctele din mulțimea .
Mai mult pentru toți x unde derivata este definită. Rezultă că funcția inversă este derivabilă în toate punctele și că
oricare ar fi x în mulțimea care este densă în intervalul . Astfel g admite o primitivă G. Pe de altă parte, nu se poate ca
fiindcă pentru orice partiție , se pot alege puncte intermediare pentru suma Riemann din mulțimea , care dau valoarea 0 sumei. Rezultă că g are mulțimea de discontinuități cu măsură Lebesgue pozitivă. Figura 1 din dreapta arată o aproximare a graficului g(x) unde iar seria este trunchiată la 8 termeni. Figura 2 arată graficul unei aproximări a primitivei G(x), și ea trunchiată la 8 termeni. Pe de altă parte dacă integrala Riemann este înlocuită de integrala Lebesgue, atunci lema lui Fatou sau teorema convergenței dominate arată că g satisface teoreme fundamentală în acest context.
- În exemplele 3 și 4, mulțimile de discontinuități ale funcțiilor g sunt dense doar într-un interval deschis finit . Totuși aceste exemple pot fi ușor modificate pentru a avea mulțimi de discontinuități dense pe întreaga dreaptă reală . Let
- Printr-o metodă similară cu cea din exemplul 5, se poate modifica g în exemplul 4 ca să dispară pentru toate numerele raționale. Dacă se folosește o versiune simplificată a integralei Riemann definită ca limita sumelor Riemann sums la stânga sau ka dreapta pe partiții regulate, se va obține că integrala unei astfel de funcții g peste un interval este 0 oricând a și b sunt ambele raționale, în loc de . Astfel teorema fundamentală eșuează spectaculos.
Note explicative[modificare | modificare sursă]
- ^ Primitivele se mai numesc și integrale generale, și uneori simplu integrale. Cel din urmă termen este generic, și nu se referă doar la integralele nedefinite (primitive), ci și la integralele definite. Când este utilizat cuvântul integrală, fără alte specificații, cititorul trebuie să deducă din context dacă referirea este la o integrală definită sau nedefinită. Unii autori definesc integrala nedefinită a unei funcții ca fiind mulțimea tuturor primitivelor posibile ale acesteia. Alții o definesc ca fiind un element ales arbitrar din acea mulțime. Wikipedia adoptă această din urmă abordare.
- ^ Funcțiile elementare includ polinomialele, exponențialele, logaritmii, trigonometricele, funcțiile trigonometrice inverse și combinările acestora
Bibliografie[modificare | modificare sursă]
- en Introduction to Classical Real Analysis, by Karl R. Stromberg; Wadsworth, 1981 (see also)
- en Historical Essay On Continuity Of Derivatives, by Dave L. Renfro; http://groups.google.com/group/sci.math/msg/814be41b1ea8c024









![{\displaystyle x_{i}^{*}\in [x_{i-1},x_{i}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dafeab86f1179399f11208ee27a15c76434aed3d)
![{\displaystyle \sum _{i=1}^{n}f(x_{i}^{*})(x_{i}-x_{i-1})=\sum _{i=1}^{n}[F(x_{i})-F(x_{i-1})]=F(x_{n})-F(x_{0})=F(b)-F(a)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f5e5c82270a166e34af6d821a0f972a4df224bcd)





















![{\displaystyle \left[F\left(-1\right),F\left(1\right)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d88b86159b2de44129d7b94b54e378bffa15a96d)







![{\displaystyle \left[a,b\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f30926fb280a9fdf66fd931e14d4363cb824feaa)
