Derivă genetică
| Parte a seriei |
| Biologie evolutivă |
|---|
 Cintezele lui Darwin de John Gould |
|
Istoria teoriei evolutive |
|
Domenii și aplicații
|
|
Implicații sociale |
Deriva genetică sau fluctuația genetică (în engleză genetic drift) este modificarea întâmplătoare a frecvenței alelelor unei gene într-o populație, de la o generație la alta.[1]
Alelele urmașilor sunt o mostră a alelelor părinților, iar soarta determină dacă un individ supraviețuiește și se reproduce. Frecvența alelelor într-o populație este proporția copiilor unei gene care au o anumită configurație.[2] Deriva genetică poate cauza dispariția unor alele și poate reduce variabilitatea genetică.
Atunci când există puține copii ale unei alele într-o populație, efectul derivei genetice e mai mare, iar când există mai mult copii efectul este mic. Numeroase discuții sunt purtate pe tema importaței acordate selecției naturale în raport cu procesele neutre (aleatoare), cum ar fi deriva genetică. Ronald Fisher susține că driftul genetic poartă un rol minor în evoluție. În anul 1968 Motoo Kimura a reaprins discuția cu a sa teorie neutră a evoluției moleculare, care susține că majoritatea cazurilor în care o modificare genetică se propagă într-o populație sunt cauzate de deriva genetică.[3]
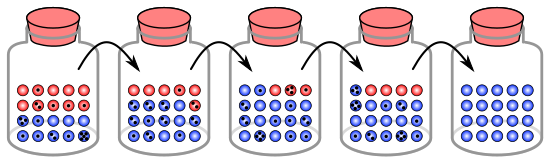
Analogia cu pietricelele dintr-un borcan[modificare | modificare sursă]
Procesul prin care se produce deriva genetică poate fi ilustrat folosind 20 de pietricele care reprezintă 20 de organisme dintr-o populație.[4]
Borcanul cu pietricele reprezintă populația inițială. Jumătate dintre pietricele sunt roșii și jumătate sunt albastre, fiecare culoare corespunzând uneia din cele două alele ale unei gene din populație. La fiecare nouă generație organismele se reproduc aleatoriu. Pentru a reprezenta reproducerea se selectează aleatoriu o pietricică din borcanul inițial și se pune o nouă pietricică cu aceeași culoare în noul borcan (pietricica selectată rămânând în borcanul inițial). Procesul este repetat până când apar 20 de noi pietricele în al doilea borcan. Al doilea borcan conține o a doua generație de urmași, care constă în 20 de pietricele de culori diferite. În afara cazului în care în al doilea borcan se află exact 10 pietricele roșii și 10 pietricele albastre, o schimbare aleatoare a avut loc în frecvența alelelor.
Procesul se repetă un anumit număr de ori, prin reproducerea unei noi generații de pietricele din generația anterioară. Numărul pietricelelor roșii și albastre fluctuează: câteodată sunt mai multe pietricele roșii și câteodată sunt mai multe pietricele albastre. Fluctuația este analoagă derivei genetice.
Se poate întâmpla ca la o anumită generație pietricelele de o anumită culoare să nu fie alese pentru a se reproduce. În acest exemplu, dacă nici o pietricică roșie nu este aleasă, borcanul care reprezintă noua generație va conține numai urmași albaștri. Alelele roșii se vor fi pierdut permanent din populație, pe când alelele albastre s-au fixat: toate viitoarele generații vor fi albastre. În cazul populațiilor de dimensiuni mici, fixarea poate avea loc în doar câteva generații.
Frecvența alelelor[modificare | modificare sursă]
Mecanismul derivei genetice poate fi ilustrat cu un exemplu simplu. Într-o colonie foarte mare de bacterii izolate dintr-o soluție, bacteriile sunt identice din punct de vedere genetic, cu excepția unei singure gene a cărei alele sunt A și B. Jumătate dintre bacterii au gena alelă A, iar cealaltă jumătate are gena alelă B. Deci atât A cât și B au frecvențele alelelor 1/2.
A și B sunt alele neutre - ele nu afectează supraviețuirea și reproducerea bacteriilor. Colonia de bacterii se micșorează într-atât încât numai patru bacterii mai au suficientă hrană. Toate celelalte bacterii din colonie mor fără a se reproduce. Există 16 combinații de alelele care pot descrie cele patru bacterii supraviețuitoare:
(A-A-A-A), (B-A-A-A), (A-B-A-A), (B-B-A-A),
(A-A-B-A), (B-A-B-A), (A-B-B-A), (B-B-B-A),
(A-A-A-B), (B-A-A-B), (A-B-A-B), (B-B-A-B),
(A-A-B-B), (B-A-B-B), (A-B-B-B), (B-B-B-B).
Combinațiile cu același număr de Auri și Buri sunt numărate și rezultă următorul tabel (probabilitățile sunt calculate luând în considerare că populația de dimensiune maximă este infinită):
| A | B | Combinații | Probabilitate |
| 4 | 0 | 1 | 1/16 |
| 3 | 1 | 4 | 4/16 |
| 2 | 2 | 6 | 6/16 |
| 1 | 3 | 4 | 4/16 |
| 0 | 4 | 1 | 1/16 |
Probabilitatea oricăi combinații posibile este
unde fracția 1/2 (probabilitatea ca A, respectiv B, să fie purtată de bacteria care supraviețuiește) este înmulțită de 4 ori(mărimea subpopulației care supraviețuiește)
După cum se poate observa din tabel, numărul total de combinații posibile care au un număr egal de Auri și Buri este 6, iar probabilitatea este 6/16. Probabilitatea de a avea un număr diferit de Auri și Buri în subpopulație este de 10/16.
Numărul de combinații posibile poate fi reprezentat folosind coeficienți binomiali care pot fi derivați din triunghiul lui Pascal. Probabilitatea oricărei combinații poate fi calculată cu formula
unde N este numărul de bacterii, iar k este numărul de alele A (sau B) din combinație.[5]
Deriva genetică are loc atunci când, în urma unor evenimente aleatoare, se schimbă frecvența alelelor dintr-o populație. În acest exemplu, populația s-a micșorat la numai 4 membri, fenomen cunoscut sub numele de Efectul „gâtului de sticlă”. Populația avea la început o distribuție egală de alele A și B, dar șansele sunt ca subpopulația supraviețuitoare de 4 bacterii să fie distribuită inegal. Probabilitatea ca subpopulația să fie supusă derivei genetice (10/16) este mai mare decât probabilitatea ca subpopulația să-și păstreze distribuția inițială (6/16).
Modele matematice ale derivei genetice[modificare | modificare sursă]
Modele matematice care descriu deriva genetică pot fi construite fie prin ecuații de difuzie , fie prin procese Markov de tipul "branching processes" (în limba engleză). [6]
Modelul Wright–Fisher[modificare | modificare sursă]
Pornim de la o genă cu două alele, A și B. În populațiile diploide cu N indivizi există 2N copii ale fiecărei gene. Un individ poate avea doua copii ale aceeași alele sau două alele diferite. Numim frecvența unei alele p, iar frecvența celeilalte alele q. Modelul Wright–Fisher (care poartă numele lui Sewall Wright și a lui Ronald Fisher) presupune că generațiile nu se suprapun și că fiecare copie din noua generație este aleasă independent și aleator din colecția de copii ale genei din vechea generație. Formula prin care se calculează probabilitatea de a obține un număr k de copii ale unei alele care a avut frecvența p în generația anterioară este [7][8]
unde simbolul "!" reprezintă funcția factorial. Această expresie mai poate fi formulată cum urmează
Modelul Moran[modificare | modificare sursă]
În modelul Moran generațiile se suprapun. La fiecare pas un individ este ales să se reproducă și un individ moare. Deci, la fiecare pas, numărul de copii ale unei alele poate crește cu 1, poate scădea cu 1 sau poate rămâne neschimbat.Matricea de transfer este tridiagonală, ceea ce înseamnă că soluțiile matematice sunt mai ușor de găsit decât în cazul modelul Wright–Fisher. Pe de altă parte, simulările pe calculator sunt mai ușor de rulat folosind modelul Wright–Fisher, pentru că necesită mai puțini pași pentru a genera o soluție. În modelul Moran o generație este prelucrată în N pași, unde N este mărimea populației. În modelul Wright–Fisher o generație este prelucrată într-un singur pas.
În practică ambele modele dau rezultate similare calitativ.
Efecte stocastice, altele decât cele datorate erorilor de eșantionare[modificare | modificare sursă]
Schimbările aleatoare ale frecvenței alelelor se pot datora și altor cauze, nu numai erorilor de eșantionare; un exemplu ar fi schimbările aleatoare ale presiunii de selecție.[9]
O altă sursă importantă de stocasticitate, poate mai importantă decât deriva genetică, este autostopul genetic .[10]
Deriva genetică și fixarea[modificare | modificare sursă]
Legea Hardy-Weinberg susține că în populații suficient de mari frecvența alelelor rămâne constantă de la o generație la alta, afară de cazurile în care apar migrația, mutațiile sau selecția.[11]
Populațiile nu dobândesc alele noi prin selecție, dar selecția poate cauza dispariția unor alele deja existente. Deoarece selecția poate elimina o alelă și pentru că scăderea și creșterea frecvenței alelelor influențează distribuția alelelor, deriva genetică poate duce la uniformizarea genetică a populație de-a lungul timpului. Când o alelă are frecvența 1 (100%) se spune că ea a fost fixată în populație iar când o alelă are frecvența 0, ea a fost eliminată. Când o alelă se fixează, deriva genetică se oprește, iar frecvența alelelor nu se poate schimba decăt dacă o noua alelă este introdusă fie prin migrație, fie prin mutație. Chiar și atunci când deriva genetică apare ca un proces aleator, în timp ea elimină variația genetică.[12]
Variația frecvenței alelelor datorată derivei genetice[modificare | modificare sursă]

Presupunând că deriva genetică este singura forță care acționează asupra unei alele, după t generații, pornind de la frecvențele p și q, variația frecvenței alelelor în populație este
Deriva genetică și selecția naturală[modificare | modificare sursă]
Legea numerelor mari susține că într-o populație mare deriva genetică nu provoacă schimbări semnificative. Într-o populație mică, erorile de eșantionare pot modifica frecvența alelelor în mod semnificativ. Deci, deriva genetică este un mecanism evolutiv cu efecte majore în populațiile mici.[14]
Cu toate că ambele procese afectează cursul evoluției, deriva genetică acționează în mod aleatoriu, în timp ce selecția naturală nu este aleatoare. În timp ce selecția naturală este direcționată, ghidând procesul evoluției spre caracteristici moștenite, care reflectă adaptarea la mediu, deriva genetică nu este direcționată și are loc numai datorită șansei, hazardului.[15] Ca un rezultat, deriva genetică acționează asupra frecvenței genelor la nivel de populație fără să țină cont de efectele fenotipice, spre deosebire de selecția naturală care favorizează genele a căror efecte fenotipice cresc șansele de reproducere și supraviețuire.[16]
Vezi și[modificare | modificare sursă]
Referințe și note[modificare | modificare sursă]
- ^ „Definiție”. DEX online. Accesat în .
- ^ Futuyma, Douglas (). Evolutionary Biology. Sinauer Associates. p. Glossary. ISBN 0-87893-189-9.
- ^ Futuyma, Douglas (). Evolutionary Biology. Sinauer Associates. p. 320. ISBN 0-87893-189-9.
- ^ „Evoluția 101:Eroarea datorită procesului de selecție și evoluția”. University of California Berkeley. Accesat în .
- ^ Walker J. „Introduction to Probability and Statistics”. The RetroPsychoKinesis Project. Fourmilab. Accesat în .
- ^ Wahl L.M. (). „Fixation when N and s Vary: Classic Approaches Give Elegant New Results”. Genetics. 188 (4): 783–785. doi:10.1534/genetics.111.131748. PMC 3176088
 . PMID 21828279.
. PMID 21828279.
- ^ Daniel Hartl, Andrew Clark (). Principles of Population Genetics (ed. 4th). Sinauer Associates. p. 112. ISBN 978-0-87893-308-2.
- ^ Tian, Jianjun Paul (). Evolution algebras and their applications. Lecture Notes in Mathematics. 1921. Berlin: Springer-Verlag. p. 11. ISBN 978-3-540-74283-8. Zbl 1136.17001.
- ^ Li, Wen-Hsiung (). Fundamentals of Molecular Evolution. Sinauer Associates. p. 28. ISBN 0-87893-452-9.
- ^ Gillespie, John H. (). „Is the population size of a species relevant to its evolution?”. Evolution. 55 (11): 2161–2169. PMID 11794777.
- ^ Warren Ewens (). Mathematical Population Genetics I. Theoretical Introduction. Interdisciplinary Applied Mathematics. Springer-Verlag.
- ^ Li, Wen-Hsiung (). Fundamentals of Molecular Evolution. Sinauer Associates. p. 29. ISBN 0-87893-452-9.
- ^ Nicholas H. Barton, Derek E. G. Briggs, Jonathan A. Eisen, David B. Goldstein, Nipam H. Patel (). Evolution. Cold Spring Harbor Laboratory Press. p. 417. ISBN 0-87969-684-2.
- ^ Zimmer, Carl (). Evolution : The Triumph of an Idea. p. 364. ISBN 0-06-095850-2. Parametru necunoscut
|editura=ignorat (ajutor); Parametru necunoscut|pagina=ignorat (posibil,|pages=?) (ajutor); Parametru necunoscut|locația=ignorat (ajutor) - ^ „Natural Selection: How Evolution Works (An interview with Douglas Futuyma, see answer to question Is natural selection the only mechanism of evolution?)”. ActionBioscience.org. Accesat în .
- ^ Cavalli-Sforza, L. L.; Menozzi, Paolo; Piazza, Alberto (). The history and geography of human genes. Princeton, N.J.: Princeton University Press. p. 413. ISBN 0-691-02905-9.






