Pătrat magic
În matematică, un pătrat magic de ordinul n este o aranjare de n² numere într-un pătrat, în așa fel încât toate numerele n din aceeași coloană, rând sau diagonală să dea adunate aceeași constantă. Un pătrat magic normal conține întregii de la 1 la n²
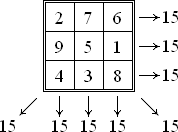
Pătrate magice exista pentru toate ordinele n ≥ 1 în afară de n = 2, deși cazul de ordine n = 1 este trivial - constă dintr-o singură celulă conținând numărul 1. Cel mai mic caz netrivial, arătat alături, este de ordinul 3.
Introducere[modificare | modificare sursă]
Fie progresia aritmetică 1, 2, 3, 4, ... 36 (pătrat de ordinul 6) și dispunerea numerelor pe două rânduri în zigzag:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 36 35 34 33 32 31 30 29 28 27 26 25 24 23 22 21 20 19
Aceasta rezultă în faptul că orice pereche de numere aliniate vertical dă aceeași sumă, știind că la deplasarea înainte în coloane numerele de sus cresc cu o unitate, pe când cele de jos scad. Suma în toate cazurile este aceea a extremelor:
Dacă se aranjează ansamblul numerelor în șase rânduri:
1 2 3 4 5 6 12 11 10 9 8 7 13 14 15 16 17 18 24 23 22 21 20 19 25 26 27 28 29 30 36 35 34 33 32 31
suma în diferitele coloane este necesar egală, fiindcă numerele sunt grupate în perechi ca și în primul caz (se pot compara perechile de rânduri 1-6, 2-5 și 3-4 cu dispunerea originală). Acum oarecum, cele trei perechi de coloane fiind (n/2), suma va fi:
ceea ce se numește constanta magică, care în cazul de față este de n×(n² + 1)/2 = 6×(36 + 1)/2 = 111.
| Ordinul n | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| M 2(n) | 15 | 34 | 65 | 111 | 175 | 260 | 369 | 505 | 671 | 870 | 1105 |
| 1 | 2 | 3 | 4 | 5 | 6 |
| 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 |
| 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 |
| 31 | 32 | 33 | 34 | 35 | 36 |
Se vede că pătratul precedent nu este un pătrat magic, pentru că aranjând numerele de manieră consecutivă, sumele cifrelor din fiecare rând cresc de fiecare dată. Există șase serii de numere între 1 și 36, a căror sumă, fără să se repete niciunul, este constanta magică. Dacă în loc de dispunerea precedentă se plasează numerele în ordine consecutivă, se obține o dispunere în care numerele din diagonala principală pot fi scrise sub forma (a-1)×n + a.
Calculând suma, rândurile a merg de la 1 la n:
Din nou constanta magică. Mai mult, orice serie de șase valori în care nu sunt două din același rând sau din aceeași coloană prin adunare va da constanta magică. Scriind termenul i, j al matricei ca (i-1)×n + j și luând șase termeni oarecare cu condiția ca nici i, nici j să nu se repete, și să varieze de la 1 la n, ecuația rezultată este aceeași ca și în cazul anterior, iar suma la fel, adică constanta magică.
Cum se și poate demonstra, numărul de serii posibile de n numere care îndeplinesc condiția anterioară este n!, 720 în pătrate de ordinul 6, și nici chiar toate sunt posibile, fiind dat că s-au obținut șase care nu sunt incluse printre ele. Prin definiție, fiind posibil să se construiască (n²)! matrice în care nici un termen să nu se repete și în care să existe cel puțin n! (de fapt mult mai multe) combinații de numere care prin adunare dau constanta magică, se înțelege intuitiv că ceea ce ar fi magic despre pătrat este că, având atâtea posibilități, să fie imposibil să se construiască un pătrat magic.
De ordinul 3 există doar un pătrat magic (variațiile diferite se pot obține prin rotație sau oglindire), în 1693 Bernard Frénicle de Bessy a stabilit că există 880 pătrate magice de ordinul 4[1], ulterior se găsiseră 275.305.334 de pătrate magice de ordinul 5; numărul de pătrate magice de ordin mai mare este necunoscut, dar după estimările lui Klaus Pinn și ale lui C. Wieczerkowski realizate în 1998 cu ajutorul metodelor Monte Carlo și ale mecanicii statistice există (1,7745 ± 0,0016) × 1019 pătrate de ordinul 6 și (3,7982 ± 0,0004) × 1034 de ordinul 7.
În ceea ce privește ordinele inferioare, este evident că de ordinul unu există numai un pătrat magic, 1 , iar de ordinul 2 nu există niciunul, ceea ce poate fi demonstrat în figura pătratului magic a, b, c, d; pentru ca această dispoziție să fie un pătrat magic ar fi trebuit să se îndeplinească următoarele ecuații (M fiind constanta magică sau orice altă cantitate, dacă este dorită):
|
|
scriind sistemul de ecuații de manieră matricială și determinând rangul matricei de coeficienți, se obține că este trei, pe când numărul de necunocute este patru, ca urmare sistemul are doar soluția trivială a = b = c = d = M/2, fiind imposibil să se construiască un pătrat magic în care cele patru cifre să fie distincte.
Istorie[modificare | modificare sursă]

Compilat prin Bao Yunlong în secolul al XIII-lea, ediția Dinastiei Ming, 1457-1463. Biblioteca Congresului SUA.
| 3 | 9 | 2 |
| 3 | 40 | 7 |
| 8 | 1 | 30 |
În China antică, se cunoșteau pătratele magice încă din Mileniul al III-lea î.Hr., după cum atestă Lo Shu. După legendă, într-o bună zi se revărsă un râu; oamenii, înfricoșați, încercară să aducă o ofrandă zeilor râului Lo (unul dintre cele revărsate) pentru a-i calma furia. Totuși, de fiecare dată când făceau aceasta, apărea o broască țestoasă care încercuia ofrandele fără să le accepte, până când un băiat își dădu seama de marcajele speciale de pe carapacea ei și așa putură să ofere cantitatea cerută (15), și să mulțumească zeul, care readuse apele la nivelul lor. Au cunoscut și combinații de această clasă indienii, arabii, egiptenii și grecii. La pătrate asemănătoare, diferitele culturi au atribuit proprietăți astrologice și divinatorii variate, fiind de numeroase ori marcate în talismane. Așa cum reia Cornelius Agrippa în Despre filozofia ocultă III (1533), pătratul de ordinul trei(15) era consacrat zeului Saturn, cel de patru(34) lui Jupiter, cel de cinci(65) lui Marte, cel de șase(111) Soare, cel de șapte(175) lui Venus, cel de opt(260) lui Mercur și cel de nouă(369)Lunei; o atribuție similară se poate găsi în astrologia hindusă.
Introducerea pătratelor magice în occident se poate atribui lui Emanuel Moschopoulos, în jurul secolului al XVI-lea, autorul unui manuscris în care pentru prima oară au fost explicate câteva metode pentru a le construi. Mai târziu, studiul proprietăților acestor pătrate a atras atenția unor mari matematicieni, care au dedicat subiectului câteva opere chiar cu toată inutilitatea practică a pătratelor magice. Printre ei se pot cita Stifel, Fermat, Pascal, Leibnitz, Frénicle de Bessy, Bachet de Méziriac, La Hire, Saurin, Euler, ... se poate zice că nici un matematician nu a putut rezista farmecelor pătratului magic.
Pătratul magic al lui Albrecht Dürer[modificare | modificare sursă]

| 16 | 3 | 2 | 13 |
| 5 | 10 | 11 | 8 |
| 9 | 6 | 7 | 12 |
| 4 | 15 | 14 | 1 |
Pătratul magic al lui Albrecht Dürer, sculptat în opera sa Melancolía este considerat primul din artele europene. În pătratul de ordinea patru se obține constanta magică (34) în rânduri, coloane, diagonale principale, și în cele patru submatrici de ordinul (2) în care se poate împărți pătratul, adăugând numerele din colțuri, cele patru numere centrale, numerele centrale ale primelor și ultimelor rânduri (sau coloane) etc. și cifrele centrale ale ultimului rând 1514 fiind anul creației operei.
|
|
|
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Câteva dispoziții în pătratul magic al lui Albrecht Dürer care se adună ca să formeze constanta magică. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Pătratul magic de la Sagrada Familia[modificare | modificare sursă]

Fațada Pasiunii a bisericii Sagrada Família în Barcelona, concepută de sculptorul Josep Subirachs arată un pătrat magic de ordinea 4:
Constanta magică a pătratului este 33, vârsta lui Iisus Cristos în timpul Pasiunii. Structural, este forte asemănătoare pătratului magic din Melancolia, dar două numere din pătrat, (12 și 16) sunt reduse cu două unități (10 și 14) iar de aceea apar repetiții. Aceasta permite să se reducă constanta magică cu 1.
Construcția Pătratelor Magice[modificare | modificare sursă]
Sunt numeroase forme de a construi un pătrat magic, dar cele mai simple consistă în a urmări anumite configurații sau formule care produc rezultate regulate. Mai mult, se poate să se impună condiții adiționale pătratului, obținându-se pătrate bimagice, trimagice etc. Prin analogie, se pot construi cercuri, poligoane și cuburi magice.
Nu există o metodă generală pentru a construi pătrate magice de orice ordin, fiind necesar să se facă distincția între cele de ordin impar, cele de ordin multiplu de 4 și restul de ordin par (4×m + 2)
Pătrate magice de ordin impar (I)[modificare | modificare sursă]
Aceste pătrate pot fi generate cu metoda publicată în 1691 de Simon de la Loubere, numită câteodată metoda siameză, metodă cunoscută de astrologii orientali. Începând în căsuța centrală a primului rând cu primul număr, umplem diagonala ruptă cu următoarele, în sens NV (sau NE). Odată umplută prima diagonală, este coborâtă de o poziție și se umple a doua în același sens ca și prima, apoi repetând pașii anteriori până se termină pătratul.
Evident, se putea începe în orice căsuță centrală a rândurilor sau coloanelor perimetrale, fiind în fiecare caz direcția diagonalelor în afara pătratului și sensul deplasării o dată terminată fiecare diagonală dat prin poziția relativă din centrul pătratului în ceea ce privește căsuța centrală.
Rezultă evident că începând cu orice altă căsuță suma rândurilor și a coloanelor va fi constanta magică, dat fiind că poziția relativă a cifrelor va fi aceeași ca și în cazul anterior; totuși, în paralela diagonală a direcției umplute nu se confirmă aceste condiție (confirmată în cealaltă). De fapt, alegerea inițială particulară a căsuței inițiale răspunde necesității ca în diagonala paralelă direcției care trebuie umplută cele cinci numere centrale ale seriei să fie plasate consecutiv dat fiind că orice alte cinci numere consecutive nu se vor aduna la constanta magică.
Pătrate magice de ordin impar (II)[modificare | modificare sursă]
| 25 | ||
| 18 | ||
| 37 |
Pasul întâi: Se scriu numerele de la 1 la n². Se scrie 1 în căsuța superioară a rombului și se urmează în formă oblică ca și în exemplul de mai jos. Pătratul magic va fi unul înscris în rombul format.
| 1 | ||||||||
| 6 | 2 | |||||||
| 11 | 7 | 3 | ||||||
| 16 | 12 | 8 | 4 | |||||
| 21 | 17 | 13 | 9 | 5 | ||||
| 22 | 18 | 14 | 10 | |||||
| 23 | 19 | 15 | ||||||
| 24 | 20 | |||||||
| 25 |
Pasul al doilea: Transferăm numerele din colțurile rombului în căsuțele goale în partea opusă a rombului.
| 1 | ||||||||
| 6 | 2 | |||||||
| 11 | 24 | 7 | 20 | 3 | ||||
| 16 | 4 | 12 | 25 | 8 | 16 | 4 | ||
| 21 | 17 | 5 | 13 | 21 | 9 | 5 | ||
| 22 | 10 | 18 | 1 | 14 | 22 | 10 | ||
| 23 | 6 | 19 | 2 | 15 | ||||
| 24 | 20 | |||||||
| 25 |
Pasul al treilea: Scoatem colțurile rombului: acum avem un pătrat magic de ordin impar.
| 11 | 24 | 7 | 20 | 3 |
| 4 | 12 | 25 | 8 | 16 |
| 17 | 5 | 13 | 21 | 9 |
| 10 | 18 | 1 | 14 | 22 |
| 23 | 6 | 19 | 2 | 15 |
Pătrate magice de ordin multiplu de 4[modificare | modificare sursă]
Se construiește un pătrat cu numerele dispuse consecutiv (să se vadă al doilea pătrat de ordinea 6 în introducere), dispoziție în care știm că suma diagonalelor este constanta magică. O dată făcut, și conservând submatricea centrală de ordinul n/2 și cele din colțuri de ordinul n/4, învârtim de 180º numerele care rămân în jurul centrului pătratului, sau, dacă se preferă sunt puse în ordin descrescător (în ambele cazuri rezultatul este același).
Plecând de la aceeași dispoziție și alegând patroane simetrice similare numerelor a fi conservate se pot construi pătrate magice diferite de cele obținute înainte, ca și următoarele:
Pătrate magice de ordin multiplu de 4n plus 2[modificare | modificare sursă]
Pentru a construi această clasă de pătrate magice se poate folosi metoda LUX. Se bazează în parte pe metoda lui la Loubere, care se folosește în construcția pătratelor magice de ordin impar (a se vedea mai sus).
Ca exemplu, o să construim un pătrat magic de latura zece.
Pasul întâi:
Regrupăm căsuțele în grupuri de 2x2, și le etichetăm pe fiecare în parte cu forma următoare:
-Pătratele din primele k+1 rânduri, unde k este împărțirea completă a mărimii pătratului în patru, sunt etichetate cu litera L (3 rânduri în cazul acesta).
-Pătratele rândului următor se etichetează cu litera U.
-Pătratele rândurilor rămase se etichetează cu litera X.
Aceste litere ne vor arăta pe urmă cum să umplem fiecare pătrat de 2x2.
| L | L | L | L | L | |||||
| L | L | L | L | L | |||||
| L | L | L | L | L | |||||
| U | U | U | U | U | |||||
| X | X | X | X | X |
Pasul al doilea:
Se schimbă pătratul U central cu pătratul L imediat superior.
| L | L | L | L | L | |||||
| L | L | L | L | L | |||||
| L | L | U | L | L | |||||
| U | U | L | U | U | |||||
| X | X | X | X | X |
Pasul al treilea
Etichetăm fiecare pătrat de 2x2 cu un număr, ghidându-ne după metoda lui la Loubere. Cu această formă indicăm în ce ordine se va umple fiecare subpătrat.
| 17 | 24 | 1 | 8 | 15 | |||||
| L | L | L | L | L | |||||
| 23 | 5 | 7 | 14 | 16 | |||||
| L | L | L | L | L | |||||
| 4 | 6 | 13 | 20 | 22 | |||||
| L | L | U | L | L | |||||
| 10 | 12 | 19 | 21 | 3 | |||||
| U | U | L | U | U | |||||
| 11 | 18 | 25 | 2 | 9 | |||||
| X | X | X | X | X |
Pasul al patrulea
Acum, subpătratului al i-lea îi corespund numerele 4i-3, 4i-2, 4i-1 și 4i. De exemplu, subpătratului 10 îi corespund numerele 37, 38, 39 și 40.
Tot ce ne mai rămâne să știm este cum să plasăm cele patru numere în subpătratul corespunzător, și aici intră în joc etichetetele LUX.
| al patrulea număr | primul număr |
| al doilea număr | al treilea număr |
| primul număr | al patrulea număr |
| al doilea număr | al treilea număr |
| primul număr | al patrulea număr |
| al treilea număr | al doilea număr |
După cum se poate vedea, literele ne spun forma pe care o iau numerele așezându-se în fiecare subpătrat.
Cu toate acesete elemente se poate construi pătratul.
| 68 | 65 | 96 | 93 | 4 | 1 | 32 | 29 | 60 | 57 |
| 66 | 67 | 94 | 95 | 2 | 3 | 30 | 31 | 58 | 59 |
| 92 | 89 | 20 | 17 | 28 | 25 | 56 | 53 | 64 | 61 |
| 90 | 91 | 18 | 19 | 26 | 27 | 54 | 55 | 62 | 63 |
| 16 | 13 | 24 | 21 | 49 | 52 | 80 | 77 | 88 | 85 |
| 14 | 15 | 22 | 23 | 50 | 51 | 78 | 79 | 86 | 87 |
| 37 | 40 | 45 | 48 | 76 | 73 | 81 | 84 | 9 | 12 |
| 38 | 39 | 46 | 47 | 74 | 75 | 82 | 83 | 10 | 11 |
| 41 | 44 | 69 | 72 | 97 | 100 | 5 | 8 | 33 | 36 |
| 43 | 42 | 71 | 70 | 99 | 98 | 7 | 6 | 35 | 34 |
Variante[modificare | modificare sursă]
Pătrate magice ezoterice[modificare | modificare sursă]
N.B. Pentru a se vedea comparările, pentru pătratele magice ezoterice, s-au luat alte culori, diferite decât cele folosite până acum.
Un pătrat magic ezoteric, folosește criterii mai restrictive în ceea ce privește condițiile unui pătrat magic, în așa fel încât să existe una pentru fiecare n. În continuare sunt descrise condițiile.
Proprietate de echivalență[modificare | modificare sursă]
| 21 | 26 |
| 25 | 27 |
| 29 | 22 |
| 8 | 1 | 6 |
| 3 | 5 | 7 |
| 4 | 9 | 2 |
În sens ezoteric, se consideră numai pătratele magice care au aceleași cifre ca și numărul căsuțelor (care urmăresc seria naturală de la 1 la n²). Pătratul din stânga nu este un pătrat magic ezoteric. În acest caz este rezultatul unui pătrat magic de n=3 a căror cifre au fost adăugate 20 (a fi comparat cu pătratul original din dreapta).
Proprietatea colțurilor[modificare | modificare sursă]
- În sens ezoteric, un pătrat magic trebuie să îndeplinească unele condiții de sumă a colțurilor lui (Pe care le numim Cifra magică-2, sau de al doilea ordin). Explicația cum se alfă:
- Dacă numim Compoziție sumarea numerelor care compun pătratul magic: C= sum (1+2+3....), sau C= ((n²+1)×(n²/2) ...
- ...și dacă numim Numărul bază (Nb) Compozăția împărțită la numărul căsuțelor care compun pătratul, vom avea Nb= C / (n²).
- Obținem și Cifra magică, Înmulțind Numărul bază cu n Cm=Nb×n (sau invers, obținem Nb, împărțind cifra magică la n Nb= Cm/n ).
| r | _ | _ | s |
| _ | _ | _ | _ |
| _ | _ | _ | _ |
| t | _ | _ | u |
| r | _ | s |
| _ | _ | _ |
| t | _ | u |
- Și fiind Cifra magică-2 suma colțurilor, atunci: Cm2= r+s+t+u
- Deci Cm2, suma colțurilor Cm2= Cm - (Nb( n-4))
- Sau (plecând de la faptul că Cm=Nb×n) : Cm2= Nb×n - (Nb(n-4)).
- Sau reducând : Cm2= 4Cm / n.
- Se semnalează în figuri căsuțele din colțuri, pentru pătrate de n=4 și n=3
- Se deduce că dacă pătratul are mai puține colțuri decât 4, atunci această cifră este adunată, și dacă este mai mare decât 4 colțuri, este scăzută. Pentru cazul în care sunt exact 4 colțuri, nici nu este adunată nici scăzută, sau adunată și scăzută,(cum este preferat să fie considerat).
- Putem să verificăm că în pătratul magic de 4 suma celor 4 colțuri Cm2 = Cm (Cifra magică-2 = Cifra magică).
Iar suma cifrelor care formează o cruce (CRUX) (cele care sunt în mijloc între două colțuri adiacente), au ca sumă Cm2. Particularitatea n = par/impar produce două cazuri.
| _ | C | _ |
| R | _ | U |
| _ | X | _ |
| _ | _ | C1 | C2 | _ | _ |
| _ | _ | _ | _ | _ | _ |
| R1 | _ | _ | _ | _ | U! |
| R2 | _ | _ | _ | _ | U2 |
| _ | _ | _ | _ | _ | _ |
| _ | _ | X1 | X2 | _ | _ |
- Pentru cazul unde n=impar: Cm2= C +R +U +X (figura din stânga)
- Și pentru cazul unde n=par cele două căsuțe adiacente care formează o cruce în aceleași condiții, doar că în acest caz fiind două grupuri de 4 căsuțe, este de două ori CM ; =2 Cm2): Cm2=(C1 +C2 +R1 +R2 + U1 +U2 +X1 +X2 )/2 (figura din dreapta)
Se arată un pătrat de n=3 ca exemplu de caz par, și unul de n=6 ca exemplu de caz impar. Să se observe că în cazul impar, se iau cele două căsuțe centrale de CRUX, motivul, pentru că trebuie împărțit după aceea în doi.
- S-a remarcat că în tablă exemplul arătat despre pătratul magic cu cazul unde n= 7 : aplicat este C=1225 ; Nb=25 ; Cm= 25×7=175 ; Cm2= 175- (25(7-4)=100
- Se poate verifica Cm2=R+S+T+U , (colțurile, în bleu deschis 22 + 4 + 46 + 28 ) = 100
- În același mod se poate verifica Cm2=C+R+U+X ,(centrele crucii, en turquoise închis 41 + 13 + 9 + 37 ) = 100
| 22 | 47 | 16 | 41 | 10 | 35 | 4 |
| 5 | 23 | 48 | 17 | 42 | 11 | 29 |
| 30 | 6 | 24 | 49 | 18 | 36 | 12 |
| 13 | 31 | 7 | 25 | 43 | 19 | 37 |
| 38 | 14 | 32 | 1 | 26 | 44 | 20 |
| 21 | 39 | 8 | 33 | 2 | 27 | 45 |
| 46 | 15 | 40 | 9 | 34 | 3 | 28 |
.
| Latura n a pătratului | Căsuțe n×n | Sumare (n²+1)×(n²/2) | Cifra magică C/n | Număr bază Cm/n | Cifra magică-2 Cm2= 4Cm / n |
| n | n² | C | Cm | Nb | Cm2 |
| 1 | 1 | 1 | 1 | 1 | 4 Non mag. |
| 2 | 4 | 10 | 5 | 2,5 | 10 Non. mág. |
| 3 | 9 | 45 | 15 | 5 | 20 |
| 4 | 16 | 136 | 34 | 8,5 | 34 |
| 5 | 25 | 325 | 65 | 13 | 52 |
| 6 | 36 | 666 | 111 | 18,5 | 74 |
| 7 | 49 | 1225 | 175 | 25 | 100 |
| 8 | 64 | 2080 | 260 | 32,5 | 130 |
| 9 | 81 | 3321 | 369 | 41 | 164 |
- Se poate înțelege că pătratul de 1 nu are 4 colțuri, și totodată a lui cifră magică-2, este 4, nefiind posibil să se adune mai mult decât 1, nu poate fi un pătrat magic ezoteric.
- Pătratul de doi, chiar dacă are 4 colțuri, a lui cifră magică-2 face să apară un rezultat de 10, ceea ce este imposibil să rezulte. Se explică mai sus în acest articol de ce un pătrat magic n=2, nu poate fi (Cm nu are rezultat), și acum de ce nu este ezoteric.
Proprietăți poziționale[modificare | modificare sursă]
Ceea ce face ca un pătrat magic ezoteric să fie ordonat sunt îndeplinirea unor alte condiții care sunt lejer diferite în pătratele cu n-par pe lângă cele cu n-impar. (același pătrat rotit sau reflectat nu mai rămâne ordonat dar continuă să fie ezoteric.
- n-impar: Nb ocupă căsuța centrală. Cifra cea mai mare este în susul căsuței centrale și cea mai mică dedesubt. Colțul r este ocupat de cifra Nb-(n/2-(1/2)) și colțul opus u de cifra Nb+(n/2-(1/2)). Colțul s este ocupat de cifra n/2+(1/2) și căsuța opusă t, de 2×Nb-(cifra s), sau, ceea ce dă același rezultat, de cifra cea mai mare a pătratului magic, - (n/2-(1/2)).
- n-par : Căsuța r (prima), este ocupată de cifra n, cifra 1 ocupă căsuța s, și ultima cifră, diagonala t, și căsuța u=t+s-r. Dacă este par, nu există căsuță centrală, și pentru același Nb, nu este întreg, și nu ocupă nici o căsuță.
Pătratul magic Renato[modificare | modificare sursă]
| 1 | 399 | 3 | 397 | 396 | 395 | 7 | 8 | 9 | 391 | 390 | 12 | 13 | 14 | 386 | 385 | 384 | 18 | 382 | 20 |
| 21 | 22 | 23 | 377 | 376 | 375 | 374 | 28 | 29 | 371 | 370 | 32 | 33 | 367 | 366 | 365 | 364 | 38 | 39 | 40 |
| 41 | 359 | 43 | 357 | 45 | 46 | 354 | 48 | 352 | 351 | 350 | 349 | 53 | 347 | 55 | 56 | 344 | 58 | 342 | 60 |
| 61 | 62 | 63 | 64 | 336 | 335 | 334 | 68 | 332 | 331 | 330 | 329 | 73 | 327 | 326 | 325 | 77 | 78 | 79 | 80 |
| 81 | 319 | 83 | 317 | 85 | 315 | 87 | 88 | 312 | 311 | 91 | 309 | 308 | 307 | 306 | 96 | 97 | 98 | 99 | 301 |
| 300 | 102 | 103 | 104 | 296 | 106 | 294 | 108 | 292 | 291 | 290 | 289 | 113 | 287 | 115 | 285 | 117 | 118 | 119 | 281 |
| 121 | 279 | 123 | 277 | 276 | 275 | 127 | 128 | 129 | 271 | 270 | 132 | 133 | 134 | 266 | 265 | 264 | 138 | 262 | 140 |
| 141 | 259 | 143 | 257 | 256 | 146 | 147 | 148 | 252 | 150 | 250 | 249 | 153 | 247 | 246 | 245 | 244 | 158 | 159 | 160 |
| 161 | 239 | 238 | 237 | 236 | 235 | 234 | 233 | 169 | 231 | 170 | 172 | 173 | 174 | 175 | 176 | 177 | 178 | 222 | 180 |
| 200 | 199 | 198 | 197 | 196 | 195 | 194 | 193 | 212 | 190 | 191 | 209 | 208 | 207 | 206 | 205 | 204 | 203 | 202 | 201 |
| 220 | 219 | 218 | 217 | 216 | 215 | 214 | 213 | 192 | 210 | 211 | 189 | 188 | 187 | 186 | 185 | 184 | 183 | 182 | 181 |
| 240 | 162 | 163 | 164 | 165 | 166 | 167 | 168 | 229 | 171 | 230 | 232 | 228 | 227 | 226 | 225 | 224 | 223 | 179 | 221 |
| 260 | 142 | 258 | 144 | 145 | 255 | 254 | 248 | 149 | 251 | 151 | 152 | 253 | 154 | 155 | 156 | 157 | 243 | 242 | 241 |
| 280 | 122 | 278 | 124 | 125 | 126 | 267 | 273 | 272 | 130 | 131 | 269 | 268 | 274 | 135 | 136 | 137 | 263 | 139 | 261 |
| 101 | 299 | 298 | 297 | 105 | 286 | 107 | 293 | 109 | 110 | 111 | 112 | 288 | 114 | 295 | 116 | 284 | 283 | 282 | 120 |
| 320 | 82 | 318 | 84 | 305 | 86 | 314 | 313 | 89 | 90 | 310 | 92 | 93 | 94 | 95 | 316 | 304 | 303 | 302 | 100 |
| 340 | 339 | 338 | 324 | 65 | 66 | 67 | 333 | 69 | 70 | 71 | 72 | 328 | 74 | 75 | 76 | 337 | 323 | 322 | 321 |
| 360 | 42 | 343 | 44 | 356 | 355 | 47 | 353 | 49 | 50 | 51 | 52 | 348 | 54 | 346 | 345 | 57 | 358 | 59 | 341 |
| 380 | 362 | 378 | 24 | 25 | 26 | 27 | 373 | 372 | 30 | 31 | 369 | 368 | 34 | 35 | 36 | 37 | 363 | 379 | 361 |
| 381 | 2 | 398 | 4 | 5 | 6 | 394 | 393 | 392 | 10 | 11 | 389 | 388 | 387 | 15 | 16 | 17 | 383 | 19 | 400 |
Acesta este pătratul magic "RENATO" al cărui autor este Jorge Egúsquiza Loayza. Acest pătrat magic care conține numerele de la 1 la 400 are suma de 4010 în direcțiile orizontale, verticale și diagonale. Crearea lui a fost posibilă folosind o metodă de creat pătrate magice de dimensiuni mari. Această metodă se bazează pe extrapolarea numerelor folosind o succesiune logică de inversare, unde se schimbă un număr superior cu unul inferior:
Numărul 2 de pe prima linie se inversează, schimbându-l cu numărul 382, care ia locul numărului 19, care trece în locul lui 399, și care se termină în căsuța numărului 2. Este o metodă logică de inversare a colțurilor.
Note[modificare | modificare sursă]
- ^ Magische Quadrate, artype.de, accesat 1 decembrie 2021






