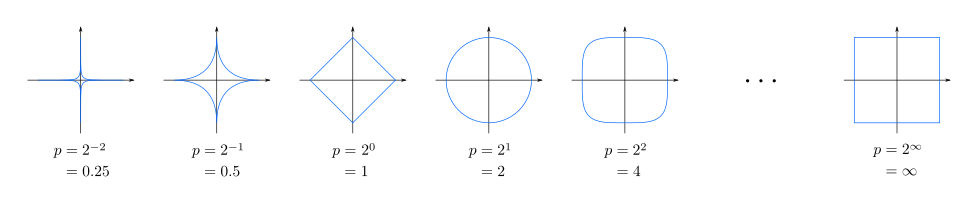Distanță Minkowski

Nu confundați cu metrica pseudoeuclidiană a spațiului Minkowski

Distanța Minkowski sau metrica Minkowski este o metrică într-un spațiu vectorial normat, care poate fi considerată ca o generalizare atât a distanței euclidiene, cât și a distanței Manhattan. Este numită după matematicianul german Hermann Minkowski.

Definiție[modificare | modificare sursă]

Distanța Minkowski de ordinul $p$ (unde $p$ este un întreg) între două puncte

X=(x_{1},x_{2},\ldots ,x_{n}){\text{ and }}Y=(y_{1},y_{2},\ldots ,y_{n})\in \mathbb {R} ^{n}

este definită drept:^[1]

D\left(X,Y\right)=\left(\sum _{i=1}^{n}|x_{i}-y_{i}|^{p}\right)^{\frac {1}{p}}.

Pentru

p\geq 1,

distanța Minkowski este metrica care rezultă din inegalitatea lui Minkowski. Când

p<1,

distanța între

(0,0)

și

(1,1)

este

2^{1/p}>2,

dar punctul

(0,1)

este la distanța

1

de ambele aceste puncte. Deoarece aceasta nu corespunde inegalității triunghiului, pentru

p<1

nu este o metrică. Totuși pentru aceste valori se poate obține o metrică prin simpla omitere a exponentului

1/p.

Metrica rezultantă este o F-normă.

De obicei distanța Minkowski este folosită cu $p$ 1 sau 2, care corespund distanței Manhattan, respectiv distanței euclidiene. În cazul limită când $p$ tinde la infinit, se obține distanța Cebîșev:^[2]

\lim _{p\to \infty }{\left(\sum _{i=1}^{n}|x_{i}-y_{i}|^{p}\right)^{\frac {1}{p}}}=\max _{i=1}^{n}|x_{i}-y_{i}|.

Similar, când $p$ tinde spre infinitul negativ, se obține:

\lim _{p\to -\infty }{\left(\sum _{i=1}^{n}|x_{i}-y_{i}|^{p}\right)^{\frac {1}{p}}}=\min _{i=1}^{n}|x_{i}-y_{i}|.

Distanța Minkowski poate fi văzută și ca un multiplu al mediei generalizate a diferențelor dintre componentele $P$ și $Q.$

Următoarele figuri arată cercurile unitare (mulțimea tuturor punctelor care se află la distanța de o unitate față de centru) pentru diferite valori ale $p$ :