Versinus
Versin or sinus versus, versin(θ), este o funcție trigonometrică egală cu 1 − cos(θ). Funcția versin apare în câteva tabele trigonometrice timpurii fiind larg răspândită, dar în ziua de azi puțin folosită.
De asemenea mai se scrie ca vers(θ) or ver(θ). În Latină, este cunoscută ca sinus versus (sinus invers) sau sagitta (săgeată).
Funcții similare[modificare | modificare sursă]
Există alte șapte funcții similare:
- Cosinus versus, sau vercosin, scrisă
- Sinus coversus, sau coversin, scrisă and sometimes abbreviated to
- Cosinus coversus, sau covercosin, scrisă
- Sinus haversus, sau haversin, scrisă , foarte cunoscută ca haversine formula și istoric folosită în navigație
- Cosinus haversus, sau havercosin, scrisă
- Sinus hacoversus, numită și hacoversin sau cohaversin, scrisă
- Cosnus hacoversus, numită și hacovercosin sau cohavercosin, scrisă
Altă funcție similară este exsecanta.
Construcția funcției versin și funcții similare[modificare | modificare sursă]
Pentru o funcție trigonometrică f, definițiile de mai sus corespund relațiilor:
Definiții[modificare | modificare sursă]
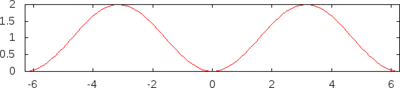
| |

| |
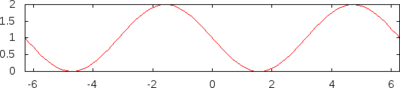
| |
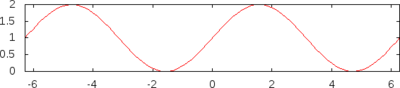
| |

| |

| |

| |

|
Derivate și integrale[modificare | modificare sursă]
Istorie și aplicații[modificare | modificare sursă]
Istoric, sinus versus a fost considerată una din cele mai importante funcții trigonometrice, dar în timpurile moderne a scăzut în popularitate datorită calculatoarelor de mână și computerelor. Când θ tinde către zero, versin(θ) este diferența dintre două mărimi foarte apropiate, deci, un utilizator al tabelului funcției cosinus are nevoie de o mare acuratețe pentru a obține funcția versin, fiind nevoit să facă tabele separate corespunzătoare. Chiar și cu calculatoarele moderne este de preferat ca pentru unghiuri θ mici să se folosească sin2. Un alt avantaj istoric al funcției versin este acela că întotdeauna este pozitivă, deci logaritmul funcției este definit pe tot domeniul cu excepția unghiurilor (θ = 0, 2π,...) unde este zero— astfel că se pot folosi tabelele logaritmice pentru înmulțiri în formulele care implică versin.
În particular, funcția haversin era importantă în navigație deoarece apare în formula haversin, care este folosită pentru calculul precis al distanțelor pe sferă atunci când sunt date pozițiile unghiulare, adică longitudinea și latitudinea. Aparent, termenul haversin, a fost născocit în textele de navigație doar pentru acest tip de aplicații (vezi referințele).
De fapt, cel mai vechi tabel care a supraviețuit, din secolele patru – cinci ale perioadei Siddhantas din India, a fost un tabel de valori numai pentru sinus și sinus versus (între 0 și 90° cu increment de 3.75°) (Boyer, 1991). Acest lucru este, poate, chiar mai surprinzător având în vedere că versin apare ca un pas intermediar în aplicarea formulei unghiului pe jumătate sin2(θ/2) = versin(θ)/2, obținută de Ptolemeu, și folosită pentru a construi astfel de tabele.
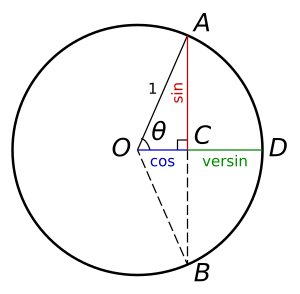
Ca și pentru sinus, etimologia derivată din secolul al 12-lea a transcris greșit cuvântul sanscrit jiva via limba arabă. Pentru a contrasta cu sinus versus, funcția sinus era numită câteodată sinus rectus sau sin vertical. Sensul acestor termeni poate fi determinat privind funcțiile în contextul lor original de definire (cercul unitate din dreapta). Pentru coarda verticală AB din cercul unitate, sinusul unghiului θ este distanța AC (jumătare din coardă). Pe de altă parte, sinus versus de θ este distanța CD de la centrul corzii la centrul arcului. Astfel, suma cos(θ) = OC și versin(θ) = CD este egală cu raza cercului OD = 1. În acest fel, sinusul este vertical (rectus) în timp ce versin este orientat pe latura sa (versus); amândouă fiind distanțe de la C la cerc.
Figura alăturată arată de asemenea motivul pentru care, uneori, versin a fost numită sagitta (săgeata), în arabă sahem cu aceeași semnificație. Dacă arcul ADB este văzut ca arma numită arc, iar coarda AB drept coarda lui, atunci versin CD este clar săgeata lui.
Mai mult, ținând de interpretarea lui sinus ca „vertical” și sinus versus ca „orizontal”, săgeata este un sinonim ieșit din uz pentru abscisă.
Funcția versin din primul cadran (0 < θ < π/2), sau haversin, sunt de asemenea folosite în mod obișnuit în procesarea semnalelor și teoria controlului ca formă a unui semnal pulsatoriu sau a unei funcții fereastră, deoarece funcția continuă este netedă ca valoare și pantă, iar valoarea ei pleacă din zero, ajunge la unu și se reîntoarce iar în zero (haversin).
"Versinus" pentru curbe arbitrare și corzi[modificare | modificare sursă]
Termenul de versin este folosit câteodată pentru a descrie deviația de la rectiliniaritate a unei curbe arbitrare plane, pentru care cercul de mai sus este un caz special. Fiind dată o coardă între două puncte ale unei curbe, distanța perpendiculară v de la coardă la curbă (uzual la mijlocul corzii) se numește măsura versin. Pentru o linie dreaptă, versinul oricărei corzi este zero, deci aceasta este măsura care caracterizează rectiliniaritatea unei curbe. La limită când lungimea corzii tinde la zero, raportul 8v/L2 tinde către curbura instantanee a curbei. Acest lucru este deosebit de util în transportul feroviar în care descrie măsura rectiliniarității liniei ferate (Nair, 1972) și este baza de calcul din metoda Hallade pentru controlul liniei. Termenul sagitta este folosit și în optică pentru a descrie suprafața lentilelor și a oglinzilor.
Vezi și[modificare | modificare sursă]
Referințe[modificare | modificare sursă]
- Boyer, Carl B. (). A History of Mathematics (ed. 2nd). New York: Wiley.
- "sagitta". Oxford English Dictionary. Oxford University Press. 2nd ed. 1989.
- Miller, J. „Earliest known uses of some of the words of mathematics (v)”.
- Calvert, James B. „Trigonometry”.
- "haversine". Oxford English Dictionary. Oxford University Press. 2nd ed. 1989. Cites coinage by Prof. Jas. Inman, D. D., in his Navigation and Nautical Astronomy, 3rd ed. (1835).
- Nair, Bhaskaran (). „Track measurement systems—concepts and techniques”. Rail International. 3 (3): 159–166. ISSN 0020-8442.
- Eric W. Weisstein, Versine la MathWorld.
- Eric W. Weisstein, Haversine la MathWorld.

































