Poliedru omnitrunchiat
| Deși acest articol conține o listă de referințe bibliografice, sursele sale rămân neclare deoarece îi lipsesc notele de subsol. Puteți ajuta introducând citări mai precise ale surselor. Întrucât este un articol tradus, a se vedea pagina de discuție, iar articolul de origine nu are nici el note de subsol, puteți ajuta și supraveghind acel articol, iar când acolo apar note de subsol, copiați-le și aici. |
În geometrie un poliedru omnitrunchiat este un Poliedru cvasiregulat trunchiat. Când astfel de poliedre sunt alternate, ele produc poliedre snub.
Toate poliedrele omnitrunchiate sunt zonoedre. Ele au simbolul Wythoff p q r | și figura vârfului 2p.2q.2r.
În general, în notația Conway a poliedrelor omnitrunchierea este un operator de teșire.
Lista poliedrelor omnitrunchiate convexe[modificare | modificare sursă]
Există trei forme convexe. Ele pot fi văzute ca fețele roșii ale unui poliedru regulat, fețele galbene sau verzi ale poliedrului dual și fețele albastre la vârfurile trunchiate ale poliedrului cvasiregulat.
| Simbol Wythoff p q r | |
Poliedru omnitrunchiat | Poliedru regulat/cvasiregulat |
|---|---|---|
| 3 3 2 | |  Octaedru trunchiat |
   Tetraedru / Octaedru / Tetraedru |
| 4 3 2 | | 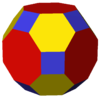 Cuboctaedru trunchiat |
   Cub / Cuboctaedru / Octaedru |
| 5 3 2 | |  Icosidodecaedru trunchiat |
   Dodecaedru / Icosidodecaedru / Icosaedru |
Lista poliedrelor omnitrunchiate neconvexe[modificare | modificare sursă]
Există 5 poliedre uniforme neconvexe omnitrunchiate.
| Simbol Wythoff p q r | |
Poliedru stelat omnitrunchiat | Simbol Wythoff p q r | |
Poliedru stelat omnitrunchiat |
|---|---|---|---|
| Domeniul triunghiurilor dreptunghice (r=2) | Domeniul triunghiurilor oarecare | ||
| 3 4/3 2 | |  Marele cuboctaedru trunchiat |
4 4/3 3 | |  Cuboctaedru cubitrunchiat |
| 3 5/3 2 | |  Marele icosidodecaedru trunchiat |
5 5/3 3 | |  Dodecadodecaedru icositrunchiat |
| 5 5/3 2 | |  Dodecadodecaedru trunchiat | ||
Alte poliedre neconvexe cu un număr par de laturi[modificare | modificare sursă]
Există 7 forme neconvexe cu simboluri Wythoff mixte „p q (r s) |’’ și figura vârfului în formă de papion, 2p.2q.-2q.-2p. Ele nu sunt adevărate poliedre omnitrunchiate: adevăratele omnitrunchiate p q r | sau p q s | au fețe coincidente 2r-gonale, respectiv 2s-gonale, care trebuie îndepărtate pentru a forma un poliedru propriu. Toate aceste poliedre sunt unilaterale, adică neorientabile. Simbolurile Wythoff degenerate p q r | sunt listate primele, urmate de simbolurile Wythoff mixte reale.
| Poliedru omnitrunchiat | Imagine | Simbol Wythoff |
|---|---|---|
| Cubohemioctaedru | 
|
3/2 2 3 | 2 3 (3/2 3/2) | |
| Micul rombihexaedru | 
|
3/2 2 4 | 2 4 (3/2 4/2) | |
| Marele rombihexaedru | 
|
4/3 3/2 2 | 2 4/3 (3/2 4/2) | |
| Micul rombidodecaedru | 
|
2 5/2 5 | 2 5 (3/2 5/2) | |
| Micul dodecicosaedru | 
|
3/2 3 5 | 3 5 (3/2 5/4) | |
| Rombicosaedru | 
|
2 5/2 3 | 2 3 (5/4 5/2) | |
| Marele dodecicosaedru | 
|
5/2 5/3 3 | 3 5/3 (3/2 5/2) | |
| Marele rombidodecaedru | 
|
3/2 5/3 2 | 2 5/3 (3/2 5/4) | |
Omnitrunchieri generale (teșire)[modificare | modificare sursă]
Omnitrunchierile mai sunt numite și cantitrunchieri sau rectificări trunchiate (tr) sau operatorul de teșire Conway (în engleză bevel – b). Când se aplică poliedrelor neregulate, pot fi generate noi poliedre, de exemplu aceste 2-poliedre uniforme:
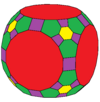
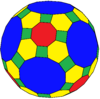
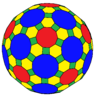
| Coxeter | trrC | trrD | trtT | trtC | trtO | trtI |
|---|---|---|---|---|---|---|
| Conway | baO | baD | btT | btC | btO | btI |
| Imagine | 
|

|

|
|
|
|
Bibliografie[modificare | modificare sursă]
- en Coxeter, Harold Scott MacDonald; Longuet-Higgins, M. S.; Miller, J. C. P. (), „Uniform polyhedra”, Philosophical Transactions of the Royal Society of London. Series A. Mathematical and Physical Sciences, 246 (916): 401–450, doi:10.1098/rsta.1954.0003, ISSN 0080-4614, JSTOR 91532, MR 0062446
- en Wenninger, Magnus (). Polyhedron Models. Cambridge University Press. ISBN 0-521-09859-9.
- en Skilling, J. (), „The complete set of uniform polyhedra”, Philosophical Transactions of the Royal Society of London. Series A. Mathematical and Physical Sciences, 278 (1278): 111–135, doi:10.1098/rsta.1975.0022, ISSN 0080-4614, JSTOR 74475, MR 0365333
- en Har'El, Z. Uniform Solution for Uniform Polyhedra., Geometriae Dedicata 47, 57-110, 1993. Zvi Har’El, Kaleido software, Images, dual images
- en Mäder, R. E. Uniform Polyhedra. Mathematica J. 3, 48-57, 1993.
| Operatori poliedrici | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Sămânță | Trunchiere | Rectificare | Bitrunchiere | Dual | Expandare | Omnitrunchiere | Alternări | ||

|

|

|

|

| |||||
| t0{p,q} {p,q} |
t01{p,q} t{p,q} |
t1{p,q} r{p,q} |
t12{p,q} 2t{p,q} |
t2{p,q} 2r{p,q} |
t02{p,q} rr{p,q} |
t012{p,q} tr{p,q} |
ht0{p,q} h{q,p} |
ht12{p,q} s{q,p} |
ht012{p,q} sr{p,q} |

