Mulțimea lui Mandelbrot

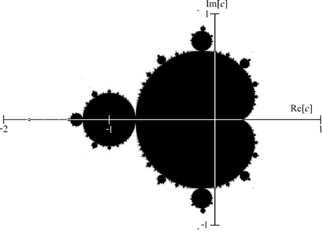
Mulțimea lui Mandelbrot este un fractal care a devenit cunoscut în afara matematicii atât pentru estetica sa, cât și pentru structura complicată, care are la bază o definiție simplă. Acest lucru se datorează în mare parte eforturilor lui Benoît Mandelbrot și ale altora de a populariza acest domeniu al matematicii. Mulțimea lui Mandelbrot se definește ca fiind mulțimea acelor puncte c din planul complex pentru care aplicând în mod repetat polinomul complex z2 + c (pornind de la z = 0) rezultatul rămâne în interiorul unui disc de rază finită.
Istoric[modificare | modificare sursă]
Mulțimea lui Mandelbrot își are locul în studiul sistemelor dinamice în planul complex, un câmp investigat pentru prima dată de către matematicienii francezi Pierre Fatou și Gaston Julia la începutul secolului 20. Primele imagini au fost desenate în 1978 de către Brooks și Matelski ca parte a studiului grupurilor Kleinian.[1]
Mandelbrot a studiat parametrul spațiu al polinoamelor pătratice într-un articol care a apărut în 1980.[2] Studiul matematic al mulțimii lui Mandelbrot a început abia cu munca matematicienilor Adrien Douady și John H. Hubbard,[3] care au stabilit multe proprietăți fundamentale ale lui și au numit mulțimea în onoarea lui Mandelbrot.
Munca lui Douady și a lui Hubbard a coincis cu un interes crescut față de dinamica complexă, iar studiul mulțimii lui Mandelbrot a fost în centrul acestui domeniu încă de atunci. Este de prisos să alcătuim o listă cu matematicienii care au contribuit la o mai bună înțelegere a mulțimii de atunci, dar o astfel de listă i-ar include cu siguranță pe Mikhail Lyubich[4][5], Curt McMullen, John Milnor, Mitsuhioo
o Shishikura și Jean-Christophe Yoccoz.
Definiție formală[modificare | modificare sursă]
Mulțimea lui Mandelbrot este definită de o familie de polinoame pătratice complexe
date de
unde este un parametru complex. Pentru fiecare , se consideră șirul obținut prin iterarea funcției începând cu , care ori tinde către infinit, ori rămâne în interiorul unui disc de rază finită. Mulțimea lui Mandelbrot este definită ca mulțimea punctelor astfel încât șirul anterior nu tinde către infinit.
Mai formal, dacă denotă a n-a iterație a funcției ( compusă cu ea de n ori) mulțimea lui Mandelbrot este submulțimea planului complex dată de
Matematic, mulțimea lui Mandelbrot este doar o mulțime de numere complexe. Un număr complex dat aparține sau nu lui . O imagine a mulțimii lui Mandelbrot poate fi creată prin colorarea punctelor care aparțin lui cu negru și a celorlalte cu alb. Imaginile colorate văzute de obicei sunt generate prin colorarea punctelor care nu aparțin mulțimii în concordanță cu cât de repede șirul diverge spre infinit. Vezi secțiunea despre imagini generate de computer de mai jos pentru detalii.
Mulțimea Mandelbrot poate fi de asemenea definită ca locul de conectivitate al familiei de polinoame . Așadar, este submulțimea planului complex formată din acei parametri pentru care mulțimea Julia a funcției este conexă.
Proprietăți de bază[modificare | modificare sursă]
Mulțimea lui Mandelbrot este o mulțime compactă, conținută în discul închis de rază 2 centrat în origine. De fapt, un punct aparține mulțimii lui Mandelbrot dacă și numai dacă pentru orice . Cu alte cuvinte, dacă valoarea absolută a devine mai mare decât 2, șirul va diverge către infinit.
Intersecția lui cu axa reală este intervalul . Parametrii de-a lungul acestui interval pot fi puși într-o corespondență unu-la-unu cu cei ai familiei logistice reale,
Corespondența este dată de
De fapt, această dă o corespodență între întreg spațiul parametrilor familiei logistice și cea a mulțimii lui Mandelbrot.
Suprafața mulțimii lui Mandelbrot este estimată la 1,506 591 77 ± 0,000 000 08. Mai exact, este conjecturat că este = 1,506591651…. [1]
Douady și Hubbard au arătat că mulțimea lui Mandelbrot este conexă. De fapt, ei au construit un izomorfism între complementara mulțimii lui Mandelbrot și complementul discului unitate închis. Mandelbrot a conjecturat inițial că mulțimea Mandelbrot este neconexă. Această conjectură fusese bazată pe imagini computerizate generate de programe care nu au capacitatea de a detecta filamentele fine care conectează diferitele părți ale lui . În urma unor experimente ulterioare, el și-a revizuit conjectura, afirmând că ar trebui să fie conexă.
Formula dinamică pentru uniformizarea complementarei mulțimii lui Mandelbrot, care reiese din demonstrațiile conexității lui ale lui Douady și Hubbard, este baza razelor externe ale mulțimii lui Mandelbrot. Aceste raze pot fi folosite în studiul mulțimii lui Mandelbrot în termeni combinatoriali, și formează baza parapuzzleului lui Yoccoz.
Frontiera mulțimii lui Mandelbrot este exact locul de bifurcație a familiei pătratice; adică mulțimea de parametri pentru care dinamica se schimbă brusc prin schimbări mici ale lui . Se poate construi ca mulțimea limită a unui șir de curbe algebrice(d) plane, curbele Mandelbrot, de tipul general, cunoscute drept lemniscate polinomiale. Curbele Mandelbrot sunt definite prin p0=z, pn=pn-12+z, și apoi interpretând mulțimea de puncte |pn(z)|=1 în planul complex drept o curbă în planul real cartezian de gradul 2n+1 în x și y.
Galerie de imagini ale unor secvențe mărite[modificare | modificare sursă]
Următorul exemplu al unei secvențe de imagini mărite până la o valoare a lui c selectată dă impresia unei mulțimi infinite de structuri geometrice diferite și explică câteva dintre regulile lor. Pentru a se obține ultima imagine, prima a fost mărită de aproximativ 60 000 000 000 de ori. În comparație cu un monitor obișnuit, ea reprezintă o secțiune într-o mulțime a lui Mandelbrot cu un diametru de 20 milioane de kilometri. Frontiera sa ar dezvălui o cantitate imensă de structuri fractale diferite.
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
- Start: Mulțimea lui Mandelbrot într-un mediu continuu colorat.
- Pasul 1: Spațiul dintre "cap" și "corp", numit și "valea căluților de mare".
- Pasul 2: La stânga, spirale duble, la dreapta, "căluți de mare".
- Pasul 3: "Căluț de mare" cu susul în jos. "Corpul" său este compus din 25 de "țepi", separați în 2 grupuri de câte 12 "țepi" fiecare și un "țep" care îl conectează la cardioida principală. Acestor două grupuri li se poate atribui un fel de metamorfoză a celor două "degete" ale "mâinii superioare" a mulțimii lui Mandelbrot. Așadar, numărul "țepilor" crește de la un "căluț" la altul cu 2. Punctul central se mai numește și punct Misiurewicz. Între "partea superioară a corpului" și "coadă" se poate observa o copie mică și distorsionată a mulțimii lui Mandelbrot, numit satelit.
- Pasul 4: Punctul central al sfârșitului "cozii căluțului de mare" este de asemenea un punct Misiurewicz.
- Pasul 5: Parte a "cozii". Există doar un singur drum format din structuri fine care merge prin întreaga "coadă". Acest zigzag trece prin "centrele" ale obiectelor mari cu 25 de "țepi" pe părțile interioară și exterioară ale "cozii". Mulțimea lui Mandelbrot este numită mulțime simplu conexă. Asta înseamnă că nu există insule și nici circuite în jurul unei găuri.
- Pasul 6: Satelit. Cele două "cozi" sunt începutul unei serii de coroane concentrice cu un satelit în centru.
- Pasul 7: Fiecare dintre aceste coroane este formată din "cozi" similare. Numărul lor crește cu puteri ale lui 2, un fenomen obișnuit în cazul sateliților. Drumul unic către centrul spiralei menționat la pasul 5 trece pe lângă satelit de la vârful cardioidei către vârful "antenei" de pe "cap".
- Pasul 8: "Antena" satelitului. Mai mulți sateliți de ordinul doi pot fi recunoscuți.
- Pasul 9: "Valea căluților de mare" a satelitului. Toate structurile din imaginea de la pasul 1 reapar.
- Pasul 10: Spirale duble și "căluți de mare". Spre deosebire de imaginea de la pasul 2, acestea au apendice formate din structuri asemănătoare "cozilor căluților de mare". Acest lucru demonstrează modul de legare a n+1 structuri diferite în mediul sateliților de ordinul n, aici pentru cazul cel mai simplu n=1.
- Pasul 11: Spirale duble cu sateliți de ordinul doi. Analog "căluților de mare", spiralele duble pot fi interpretate ca metamorfoză a "antenei".
- Pasul 12: În exteriorul apendicelor pot fi recunoscute insule de structuri. Au forma mulțimilor Julia Jc. Cea mai mare dintre ele poate fi găsită în centrul "cârligului dublu" din partea dreaptă.
- Step 13: Parte a "cârligului dublu".
- Pasul 14: La prima vedere, aceste insule par a fi formate dintr-un număr infinit de părți, precum mulțimile Cantor, așa cum se întâmplă în cazul mulțimilor Julia Jc corespunzătoare. Aici sunt conectate prin structuri minuscule astfel încât întregul reprezintă o mulțime simplu conexă. Aceste structuri mici se întâlnesc la un satelit central care este prea mic pentru a putea fi observat la această rezoluție. Valoarea lui c pentru Jc corespunzătoare nu este cea a centrului imaginii, ci are relativ la corpul principal al mulțimii lui Mandelbrot aceeași poziție ca și centrul acestei imagini în relație cu satelitul din imaginea de la pasul 7.
Cardioida principală și bulbii periodici[modificare | modificare sursă]

La privirea unei imagini reprezentând mulțimea lui Mandelbrot, se observă imediat regiunea în formă de cardioidă din centru. Această cardioidă principală este regiunea acelor parametri pentru care are punct fix de atracție. Este formată din toți parametrii de forma
pentru oricare din discul unitate deschis.
La stânga cardioidei principale, atașat de ea în punctul , se află un bulb circular. Bulbul este format din acei parametri pentru care are un ciclu de atracție de perioadă 2. Această mulțime de parametri este de fapt un cerc, mai precis de rază 1/4 și centru -1.
Există și un număr infinit de bulbi atașați la cardioida principală: pentru fiecare număr rațional , cu p și q coprime, există un astfel de bulb atașat la parametrul:
Acest bulb se numește bulbul al mulțimii lui Mandelbrot. Este format din acei parametri care au un ciclu de atracție de perioadă și număr de rotație combinatoric . Mai exact, toate componentele Fatou de perioadă conținând ciclul de atracție se ating într-un punct comun (denumit uzual punctul fix ). Dacă etichetăm aceste componente în sens trigonometric, atunci mapează componenta la componenta .

Schimbarea comportamentului care apare la este cunoscută ca o bifurcație: punctul de atracție fix "se lovește" cu un ciclu de respingere de perioadă . Pe măsură ce înaintăm prin parametrul de bifurcație în bulbul , punctul de atracție fix devine un punct de respingere fix (punctul fix ), iar ciclul de perioadă devine ciclu de atracție.
Componente hiperbolice[modificare | modificare sursă]
Toți bulbii întâlniți în secțiunea anterioară sunt interiori componentelor mulțimii lui Mandelbrot în care graficele au un ciclu de atracție periodic. Astfel de componente se numesc componente hiperbolice.
Este conjecturat că acestea sunt singurele regiuni interioare ale lui . Această problemă, cunoscută ca densitatea de hiperbolicitate, este probabil cea mai importantă problemă nerezolvată din câmpul dinamicii complexe. Componente non-hiperbolice ipotetice ale mulțimii lui Mandelbrot sunt denumite deseori componente "ciudate".
Pentru polinoamele pătratice reale, s-a răspuns la această întrebare în anii 1990, independent, de către Lyubich și de către Graczyk și Świątek. (Observați că acele componente hiperbolice care intersectează axa reală corespund exact ferestrelor periodice din diagrama Feigenbaum. Deci acest rezultat afirmă că astfel de fereste există lângă orice parametru din diagramă.)
Nu toate componentele hiperbolice pot fi atinse de o secvență de bifurcații directe din cardioida principală a mulțimii lui Mandelbrot. Totuși, o astfel de componentă poate fi atinsă de o secvență de bifurcații directe de la cardioida principală a unei copii mici a mulțimii lui Mandelbrot (vezi mai jos).
Copii mici ale mulțimii lui Mandelbrot[modificare | modificare sursă]

Mulțimea lui Mandelbrot este auto-similară în sensul că versiuni mici și distorsionate ale ei pot fi găsite la orice scară pe lângă orice punct al graniței mulțimii. Acest fenomen este explicat de teoria renormalizării a lui Douady și Hubbard.
Relația cu mulțimile Julia[modificare | modificare sursă]

Ca o consecință a definiției mulțimii lui Mandelbrot, există o legătură strânsă între geometria mulțimii lui Mandelbrot la un moment dat și structura mulțimii Julia corespunzătoare.
Acest principiu este exploatat în aproape toate rezultatele obținute asupra mulțimii lui Mandelbrot. De exemplu, Shishikura dovedește că, pentru o mulțime densă de parametri din granița mulțimii lui Mandelbrot, mulțimea Julia are dimensiunea Haussdorff doi, și apoi transferă această informație parametrului plan. În mod similar, Yoccoz dovedește întâi conectivitatea locală pentru mulțimile Julia, iar apoi o stabilește pentru mulțimea lui Mandelbrot cu parametrii corespunzători. Adrien Douady formulează acest principiu în felul următor:
Ară în planul dinamic și culege în spațiul parametrilor.
Geometria mulțimii lui Mandelbrot[modificare | modificare sursă]
Pentru fiecare număr rațional , unde și sunt coprime, există o componentă hiperbolică de perioadă care se bifurcă din cardioida principală. Partea mulțimii lui Mandelbrot care se conectează la cardioida principală în acest punct se numește membru-. Experimente computerizate sugerează că diametrul membrului tinde la zero precum . Cea mai bună estimare curentă este faimoasa inegalitate Yoccoz, care afirmă că mărimea tinde la zero precum .
O perioadă membru- va avea "antene" deasupra membrului. Putem astfel determina perioada bulbului dat prin numărarea acestor antene.

Generalizări[modificare | modificare sursă]
Uneori, punctele de conexitate ale familiilor altele decât cele pătratice sunt denumite și mulțimile lui Mandelbrot ale acelor familii.
Locurile de conexitate ale familiilor polinomiale unicritice pentru sunt deseori numite mulțimi Multibrot.

Pentru familii generale de funcții holomorfice, granița mulțimii lui Mandelbrot este generalizată în locul de bifurcație, care este un subiect de studiat chiar și când locul de conexitate nu este util.
De asemenea, este posibil să se considere construcții similare în studiul corespondențelor neanalitice. Un interes particular îl reprezintă tricornul, locul de conexitate al familiei anti-holomorfice
Tricornul (denumit și mulțime Mandelbar) a fost descoperit de către Milnor în studiul său despre secțiunile de parametri ai polinoamelor cubice reale. Nu este local conex. Această proprietate este moștenită de către puntul de conexitate al polinoamelor cubice reale.
Referințe[modificare | modificare sursă]
- ^ en Robert Brooks și Peter Matelski, The dynamics of 2-generator subgroups of PSL(2,C), în "Riemann Surfaces and Related Topics", ed. Kra and Maskit, Ann. Math. Stud. 97, 65–71, ISBN 0-691-08264-2
- ^ en Benoît Mandelbrot, Fractal aspects of the iteration of for complex , Annals NY Acad. Sci. 357, 249/259
- ^ fr Adrien Douady și John H. Hubbard, Etude dynamique des polynômes complexes, Prépublications mathémathiques d'Orsay 2/4 (1984 / 1985)
- ^ en Mikhail Lyubich, Six Lectures on Real and Complex Dynamics, mai-iunie 1999
- ^ en Mikhail Lyubich, Regular and stochastic dynamics in the real quadratic family, Proceedings of the National Academy of Sciences of the United States of America, vol. 95, pag. 14025-14027, noiembrie 1998
- Arthur C. Clarke's Fractals: The Colors Of Infinity (1995)















![{\displaystyle [-2;0,25]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/582bfeed93afc6c0e54a0d2ed82c938e058dfdf0)
![{\displaystyle z\mapsto \lambda z(z-1),\quad \lambda \in [1,4].\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/046eb39ad22ebc7cad68eee2ee24e41c1c08bb48)
























