Formulele lui De Morgan

Formulele lui De Morgan reprezentate cu diagrame Venn. În fiecare caz, mulțimea rezultată este mulțimea tuturor punctelor în orice nuanță de albastru.

În logica propozițională^⁠(d) și algebra booleană, formulele lui De Morgan, cunoscute și ca legile sau teoremele lui De Morgan, sunt o pereche de reguli de transformare care sunt reguli valide inferență^⁠(d). Ele sunt numite după Augustus De Morgan, un matematician britanic din secolul al XIX-lea. Regulile permit exprimarea conjuncțiilor^⁠(d) și disjuncțiilor în termeni reciproci prin negare^⁠(d).

Regulile pot fi exprimate în limbaj natural drept:

• Negația unei disjuncții este conjuncția negațiilor
• Negația unei conjuncții este disjuncția negațiilor

sau

• Complementul reuniunii a două mulțimi este același cu intersecția complementelor lor
• Complementul intersecției a două mulțimi este același cu reuniunea complementelor lor

sau

• non (A sau B) = (non A) și (non B)
• non (A și B) = (non A) sau (non B)

unde „A sau B” este „sau inclusiv” care înseamnă cel puțin unul dintre A sau B, și nu un „sau exclusiv” care înseamnă exact unul dintre A sau B.

În teoria mulțimilor și algebra booleană, acestea se scriu formal ca

${\begin{aligned}{\overline {A\cup B}}&={\overline {A}}\cap {\overline {B}},\\{\overline {A\cap B}}&={\overline {A}}\cup {\overline {B}},\end{aligned}}$

Unde

• $A$ și $B$ sunt mulțimi,
• ${\overline {A}}$ este complementul lui $A$ ,
• $\cap$ este intersecția și
• $\cup$ este reuniunea .

Echivalența lui ¬φ ∨ ¬ψ și ¬(φ ∧ ψ) este afișată în această tabelă de adevăr.

În limbajul formal, regulile se scriu ca

$\neg (P\lor Q)\iff (\neg P)\land (\neg Q),$

și

$\neg (P\land Q)\iff (\neg P)\lor (\neg Q)$

Unde

• P și Q sunt propoziții,
• $\neg$^⁠(d) este operatorul logic de negație (NON),
• $\land$^⁠(d) este operatorul logic de conjuncție (ȘI),
• $\lor$ este operatorul logic de disjuncție (SAU),
• $\iff$ este un simbol metalogic care înseamnă „poate fi înlocuit într-o demonstrație logică^⁠(d) cu”, adesea citit ca „dacă și numai dacă” sau „este echivalent cu”. Pentru orice combinație de valori adevărat/fals pentru P și Q, părțile din stânga și din dreapta ale săgeții vor păstra aceeași valoare de adevăr după evaluare.

Formulele lui De Morgan cu operația de scădere între mulțimi.

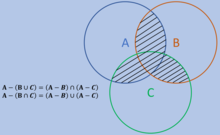
O altă formă a legilor lui De Morgan este următoarea, așa cum se vede în figura din dreapta.

$A-(B\cup C)=(A-B)\cap (A-C),$

$A-(B\cap C)=(A-B)\cup (A-C).$

Printre aplicațiile acestor formule se numără simplificarea expresiilor^⁠(d) logice în programe de calculator și proiecte de circuite digitale. Legile lui De Morgan sunt un exemplu de concept mai general al dualității matematice.

Notație formală

Regula de negație a conjuncției poate fi scrisă în notație succesivă^⁠(d):

$\neg (P\land Q)\vdash (\neg P\lor \neg Q)$ ,

și

$(\neg P\lor \neg Q)\vdash \neg (P\land Q)$ .

Regula de negație a disjuncției poate fi scrisă astfel:

$\neg (P\lor Q)\vdash (\neg P\land \neg Q)$ ,

și

$(\neg P\land \neg Q)\vdash \neg (P\lor Q)$ .

Sub formă de regulă de inferență^⁠(d): negarea conjuncției

${\frac {\neg (P\land Q)}{\therefore \neg P\lor \neg Q}}$

${\frac {\neg P\lor \neg Q}{\therefore \neg (P\land Q)}}$

și negarea disjuncției

${\frac {\neg (P\lor Q)}{\therefore \neg P\land \neg Q}}$

${\frac {\neg P\land \neg Q}{\therefore \neg (P\lor Q)}}$

și exprimată ca tautologie^⁠(d) de adevăr funcțional sau teoremă a logicii propoziționale:

${\begin{aligned}\neg (P\land Q)&\to (\neg P\lor \neg Q),\\(\neg P\lor \neg Q)&\to \neg (P\land Q),\\\neg (P\lor Q)&\to (\neg P\land \neg Q),\\(\neg P\land \neg Q)&\to \neg (P\lor Q),\end{aligned}}$

Unde $P$ și $Q$ sunt propoziții exprimate într-un sistem formal.

Forma de substituție

Legile lui De Morgan sunt prezentate în mod normal în forma compactă de mai sus, cu negarea rezultatului în stânga și negarea termenilor în dreapta. O formă mai clară de substituție poate fi enunțată astfel:

${\begin{aligned}(P\land Q)&\Longleftrightarrow \neg (\neg P\lor \neg Q),\\(P\lor Q)&\Longleftrightarrow \neg (\neg P\land \neg Q).\end{aligned}}$

Aceasta subliniază nevoia de a inversa atât intrările, cât și ieșirea, precum și de a schimba operatorul atunci când se efectuează o substituție.

Teoria mulțimilor și algebra booleană

În teoria mulțimilor și algebra booleană, este adesea menționat ca „interschimbarea de reuniunii și intersecției în raport cu complementarea”, care poate fi exprimată formal ca:

${\begin{aligned}{\overline {A\cup B}}&={\overline {A}}\cap {\overline {B}},\\{\overline {A\cap B}}&={\overline {A}}\cup {\overline {B}},\end{aligned}}$

Unde:

• ${\overline {A}}$ este negația lui $A$, bara superioară^⁠(d) fiind scrisă deasupra termenilor de negat,
• $\cap$ este operatorul de intersecție (ȘI),
• $\cup$ este operatorul de reuniune (SAU).

Reuniuni și intersecții de orice număr de mulțimi

Forma generalizată este

${\begin{aligned}{\overline {\bigcap _{i\in I}A_{i}}}&\equiv \bigcup _{i\in I}{\overline {A_{i}}},\\{\overline {\bigcup _{i\in I}A_{i}}}&\equiv \bigcap _{i\in I}{\overline {A_{i}}},\end{aligned}}$

unde I este o mulțime de indexare, care poate fi numărabil sau nenumărabil infinită.

În notația mulțimilor, legile lui De Morgan pot fi amintite folosind mnemonica^⁠(d) „rup bara, schimb semnul”.

Inginerie

În ingineria electrică și a calculatoarelor, legile lui De Morgan se scriu de regulă ca:

${\overline {(A\cdot B)}}\equiv ({\overline {A}}+{\overline {B}})$

și

${\overline {A+B}}\equiv {\overline {A}}\cdot {\overline {B}},$

Unde:

• $\cdot$ este ȘI logic,
• $+$ este SAU logic,
• bara superioară înseamnă negația logică a ceea ce este sub bară.

Căutarea în texte

Legile lui De Morgan se aplică în mod obișnuit în căutarea de texte folosind operatori booleeni AND, OR și NOT. Fie o mulțime de documente care conțin cuvintele „pisici” și „câini”. Legile lui De Morgan susțin că aceste două căutări vor returna aceeași mulțime de documente:

Căutare A: NOT (pisici OR câini)

Căutare B: (NOT pisici) AND (NOT câini)

Corpul de documente care conțin „pisici” sau „câini” poate fi reprezentat prin patru documente:

Documentul 1: Conține doar cuvântul „pisici”.

Documentul 2: Conține doar „câini”.

Documentul 3: Conține atât „pisici” cât și „câini”.

Documentul 4: Nu conține nici „pisici”, nici „câini”.

La evaluarea căutarii A, „(pisici SAU câini)”, în mod cert va returna documentele 1, 2 și 3. Deci, negarea acelei căutări (care este căutarea A) va returna orice altceva, adică documentul 4.

Evaluarea căutarii B „(NU pisici)” va returna documentele care nu conțin „pisici”, adică documentele 2 și 4. În mod similar, căutarea „(NU câini)” va returna documentele 1 și 4. Aplicarea operatorului ȘI pe aceste două căutări (Căutarea B) va returna documentele care sunt comune acestor două căutări, anume documentul 4.

O evaluare similară poate fi aplicată pentru a arăta că următoarele două căutări vor returna documentele 1, 2 și 4:

Căutarea C: NU (pisici ȘI câini),

Căutarea D: (NU pisici) SAU (NU câini).

Istorie

Formulele sunt denumite după Augustus De Morgan (1806–1871), care a introdus o versiune formală a lor în logica propozițională^⁠(d) clasică. Enunțul lui De Morgan a fost influențat de algebrizarea logicii întreprinsă de George Boole, care mai târziu a întărit meritul lui De Morgan pentru descoperirea lor. Cu toate acestea, o observație similară fusese făcută și de Aristotel și era cunoscută de logicienii greci și medievali. De exemplu, în secolul al XIV-lea, William de Ockham a notat cuvintele care ar rezulta din citirea legilor. Jean Buridan, în Summulae de Dialectica, descrie și regulile de conversie care urmează liniile formulelor lui De Morgan. Lui De Morgan i se acordă însă credit pentru enunțarea lor în termenii logicii formale moderne și încorporarea lor în limbajul logicii. Legile lui De Morgan pot fi demonstrate cu ușurință și pot părea chiar banale. Cu toate acestea, aceste legi sunt utile pentru a face inferențe valide în demonstrații și argumente deductive.

Demonstrație informală

Teorema lui De Morgan se poate aplica negației unei disjuncții sau negației unei conjuncții^⁠(d) într-o formulă sau într-o parte a unei formule.

Negarea unei disjuncții

În cazul aplicării acesteia la o disjuncție, fie următoarea afirmație: „este fals că oricare dintre A sau B este adevărat”, ceea ce se scrie astfel:

$\neg (A\lor B).$

Prin faptul că s-a stabilit că niciuna dintre A și B nu sunt adevărate, atunci trebuie să rezulte că A nu este adevărat, și^⁠(d) B nu este adevărat, ceea ce se poate scrie direct ca:

$(\neg A)\wedge (\neg B).$

Dacă A sau B ar fi adevărate, atunci disjuncția dintre A și B ar fi adevărată, făcând ca negația să fie falsă. În limbaj natural, de aici rezultă logica că „din moment ce două lucruri sunt ambele false, este și fals că oricare dintre ele este adevărat”.

Lucrând în direcția opusă, a doua expresie afirmă că A este fals și B este fals (sau echivalent că „nu A” și „nu B” sunt adevărate). Știind acest lucru, o disjuncție a lui A și B trebuie să fie și ea falsă. Negația disjuncției menționate trebuie astfel să fie adevărată, iar rezultatul este identic cu prima afirmație.

Negarea unei conjuncții

Aplicarea teoremei lui De Morgan la conjuncție este foarte asemănătoare cu aplicarea ei la o disjuncție atât ca formă, cât și ca rațiune. Fie următoarea afirmație: „este fals că A și B sunt ambele adevărate”, care se scrie:

$\neg (A\land B).$

Pentru ca această afirmație să fie adevărată, una sau ambele dintre A sau B trebuie să fie false, pentru că dacă ambele ar fi adevărate, atunci conjuncția dintre A și B ar fi adevărată, făcând ca negația să fie falsă. Astfel, unul (cel puțin) sau mai multe dintre A și B trebuie să fie false (sau echivalent, unul sau mai multe dintre „nu A” și „nu B” trebuie să fie adevărate). Aceasta se poate scrie direct:

$(\neg A)\lor (\neg B).$

În limbaj natural, aceasta urmează logica că „din moment ce este fals că două lucruri sunt ambele adevărate, cel puțin unul dintre ele trebuie să fie fals”.

Lucrând din nou în direcția opusă, a doua expresie afirmă că cel puțin unul dintre „nu A” și „nu B” trebuie să fie adevărat sau, în mod echivalent, că cel puțin unul dintre A și B trebuie să fie fals. Deoarece cel puțin unul dintre ele trebuie să fie fals, atunci conjuncția lor este și ea falsă. Negarea conjuncției menționate are ca rezultat o expresie adevărată, iar această expresie este identică cu prima afirmație.

Demonstrație formală

Aici, cu $A^{\complement }$ se notează complementul lui A. Demonstrația $(A\cap B)^{\complement }=A^{\complement }\cup B^{\complement }$ se realizează în 2 pași, în care se demonstrează că $(A\cap B)^{\complement }\subseteq A^{\complement }\cup B^{\complement }$ și $A^{\complement }\cup B^{\complement }\subseteq (A\cap B)^{\complement }$.

Partea 1

Fie $x\in (A\cap B)^{\complement }$. Atunci $x\not \in A\cap B$.

Întrucât $A\cap B=\{\,y\ |\ y\in A\wedge y\in B\,\}$, atunci $x\not \in A$ sau $x\not \in B$.

Dacă $x\not \in A$, atunci $x\in A^{\complement }$, și deci $x\in A^{\complement }\cup B^{\complement }$.

Analog, dacă $x\not \in B$, atunci $x\in B^{\complement }$, și deci $x\in A^{\complement }\cup B^{\complement }$.

Astfel, $\forall x{\Big (}x\in (A\cap B)^{\complement }\implies x\in A^{\complement }\cup B^{\complement }{\Big )}$;

adică $(A\cap B)^{\complement }\subseteq A^{\complement }\cup B^{\complement }$.

Partea 2

Pentru a demonstra reciproca, fie $x\in A^{\complement }\cup B^{\complement }$, și, prin reducere la absurd, vom presupune că $x\not \in (A\cap B)^{\complement }$.

În această ipoteză, $x\in A\cap B$,

de unde rezultă că $x\in A$ și $x\in B$, și deci $x\not \in A^{\complement }$ și $x\not \in B^{\complement }$.

Aceasta înseamnă însă că $x\not \in A^{\complement }\cup B^{\complement }$, ceea ce contrazice presupunerea că $x\in A^{\complement }\cup B^{\complement }$.

Din acest motiv, înseamnă că presupunerea că $x\not \in (A\cap B)^{\complement }$ este falsă, și deci $x\in (A\cap B)^{\complement }$.

Prin urmare, $\forall x{\Big (}x\in A^{\complement }\cup B^{\complement }\implies x\in (A\cap B)^{\complement }{\Big )}$,

adică $A^{\complement }\cup B^{\complement }\subseteq (A\cap B)^{\complement }$.

Concluzie

Dacă $A^{\complement }\cup B^{\complement }\subseteq (A\cap B)^{\complement }$ și $(A\cap B)^{\complement }\subseteq A^{\complement }\cup B^{\complement }$, atunci $(A\cap B)^{\complement }=A^{\complement }\cup B^{\complement }$; astfel se demonstrează legea lui De Morgan.

Cealaltă lege a lui De Morgan, $(A\cup B)^{\complement }=A^{\complement }\cap B^{\complement }$, se demonstrează similar.

Generalizarea dualității De Morgan

Formulele lui De Morgan reprezentate ca circuite cu porți logice (diagrame International Electrotechnical Commission).

În extensii ale logicii propoziționale clasice, dualitatea rămâne valabilă (adică oricărui operator logic i se poate găsi oricând dualul), întrucât în prezența identităților ce guvernează negarea, întotdeauna se poate introduce un care este dualul De Morgan al altuia. Aceasta conduce la o importantă proprietate a logicilor bazate pe logica clasică^⁠(d), anume existența formelor normale de negație^⁠(d): orice formulă este echivalentă cu altă formulă în care apar negații doar ca aplicate atomilor nelogici ai formulei. Existența formelor normale de negație susține multe aplicații, de exemplu în proiectarea circuitelor digitale^⁠(d), unde este folosită pentru a manipula tipurile de porți logice, și în logica formală, unde se caută forma normală conjunctivă^⁠(d) și forma normală disjunctivă^⁠(d) a unei formule. Programatorii le folosesc pe acestea pentru a simplifica sau a nega corect condiții logice^⁠(d) complicate. Adesea, ele sunt utilizate la calculele din teoria probabilității.

Dualul oricărui operator propozițional P(p, q, ...) ca funcție de propozițiile elementare p, q, ... se definește ca operatorul ${\mbox{P}}^{d}$ definit prin

${\mbox{P}}^{d}(p,q,...)=\neg P(\neg p,\neg q,\dots ).$

Extensia la logica modală și cu predicate

Această dualitate se poate generaliza și la cuantificatori, astfel că, de exemplu, cuantificatorul universal^⁠(d) și cuantificatorul existențial^⁠(d) sunt duali:

$\forall x\,P(x)\equiv \neg [\exists x\,\neg P(x)]$

$\exists x\,P(x)\equiv \neg [\forall x\,\neg P(x)]$

Pentru a pune în legătură aceste dualități de cuantificatori cu relațiile De Morgan, se alcătuiește un model^⁠(d) cu un număr mic de elemente în domeniul său D, astfel încât

D = {a, b, c}.

Atunci

$\forall x\,P(x)\equiv P(a)\land P(b)\land P(c)$

și

$\exists x\,P(x)\equiv P(a)\lor P(b)\lor P(c).$

Dar, folosind legile lui De Morgan,

$P(a)\land P(b)\land P(c)\equiv \neg (\neg P(a)\lor \neg P(b)\lor \neg P(c))$

și

$P(a)\lor P(b)\lor P(c)\equiv \neg (\neg P(a)\land \neg P(b)\land \neg P(c)),$

ceea ce confirmă dualitatea cuantificatorilor în acest model.

Apoi, dualitățile cuantificatorilor pot fi extinse mai departe în logica modală^⁠(d), punând în legătură operatorii pătrat ("este necesar ca") și caro ("este posibil ca"):

$\Box p\equiv \neg \Diamond \neg p,$

$\Diamond p\equiv \neg \Box \neg p.$

În aplicarea lor asupra modalitaților aletice^⁠(d) de necesitate și posibilitate, Aristotel a observat acest caz, și în cazul logicii modale normale^⁠(d), relațiile acestor operatori modali cu cuantificarea pot fi înțelese prin alcătuirea de modele folosind semantica Kripke^⁠(d).

În logica intuiționistă

Trei din cele patru implicații ale legilor lui De Morgan sunt valabile în logica intuiționistă^⁠(d). Anume:

$\neg (P\lor Q)\,\leftrightarrow \,{\big (}(\neg P)\land (\neg Q){\big )},$

și

${\big (}(\neg P)\lor (\neg Q){\big )}\,\to \,\neg (P\land Q).$

Reciproca ultimei implicații nu este valabilă în logica intuiționistă pură. Valoarea "fals" de adevăr a propoziției $P\land Q$ nu poate fi neapărat rezolvată prin găsirea acelui termen al conjuncției care este fals. De exemplu, dacă se știe că la întâlnirea dintre Alice și Bob nu au venit amândoi, nu se știe care dintre ei nu a venit. Acest din urmă principiu este echivalent cu principiul mijlocului exclus^⁠(d) slab ${\mathrm {WPEM} }$,

$(\neg P)\lor \neg (\neg P).$

Această formă slabă poate fi folosită ca fundamnet pentru o logică intermediară^⁠(d). Pentru versiunea rafinată a legii privind afirmațiile existențiale, vezi principiul limitat mic al omniscienței^⁠(d) ${\mathrm {LLPO} }$, care este însă diferit de principiul limitat slab al omniscienței ${\mathrm {WLPO} }$.

Celelalte trei legi ale lui De Morgan rămân valabile dacă negația $\neg P$ este înlocuită cu implicația $P\to C$ pentru un predicat arbitrar constant C, ceea ce înseamnă că legile de mai sus rămân valabile și în logica minimală^⁠(d).

Analog celor mai de sus, legile cuantificatorilor:

$\forall x\,\neg P(x)\,\leftrightarrow \,\neg \exists x\,P(x)$

și

$\exists x\,\neg P(x)\,\to \,\neg \forall x\,P(x).$

sunt tautologii chiar și în logica minimală în care negația este înlocuită cu implicația unui $Q$ fix, în vreme ce reciproca ultimei legi nu trebuie în general să fie adevărată.

Mai mult, avem:

$(P\lor Q)\,\to \,\neg {\big (}(\neg P)\land (\neg Q){\big )},$

$(P\land Q)\,\to \,\neg {\big (}(\neg P)\lor (\neg Q){\big )},$

$\forall x\,P(x)\,\to \,\neg \exists x\,\neg P(x),$

$\exists x\,P(x)\,\to \,\neg \forall x\,\neg P(x),$

dar reciproca lor implică mijlocul exclus^⁠(d), ${\mathrm {PEM} }$.

În ingineria calculatoarelor

Legile lui De Morgan sunt folosite pe scară largă în ingineria calculatoarelor și în logica digitală pentru simplificarea proiectării circuitelor.