De la Wikipedia, enciclopedia liberă
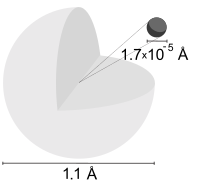
Atomul de hidrogen în tabelul nuclidelor Reprezentarea atomului de hidrogen , unde raza confirmă cea indicată de modelul atomic Bohr Atomul de hidrogen este atomul hidrogenului , care este cel mai simplu element chimic .
Este alcătuit dintr-un nucleu pozitiv compus dintr-un singur proton și un electron ce se mișcă în jurul nucleului pe o orbită închisă.
Mișcarea electronului în atomul de hidrogen (sau hidrogenoid) a fost studiată și cu metodele mecanicii cuantice .
Energia potențială a electronului este:
U
=
−
Z
e
2
4
π
ϵ
0
r
,
{\displaystyle U=-{\frac {Ze^{2}}{4\pi \epsilon _{0}r}},}
unde:
Ecuația lui Schrödinger are forma:
Δ
Ψ
+
8
π
2
m
0
h
2
(
E
+
Z
e
2
4
π
ϵ
0
r
)
Ψ
=
0
,
{\displaystyle \Delta \Psi +{\frac {8\pi ^{2}m_{0}}{h^{2}}}\left(E+{\frac {Ze^{2}}{4\pi \epsilon _{0}r}}\right)\Psi =0,}
unde:
Soluțiile în coordonate sferice sunt:
Ψ
n
l
m
=
(
1
2
π
)
1
/
2
⋅
(
2
n
r
0
)
1
/
2
⋅
(
1
2
n
π
)
1
/
2
⋅
{\displaystyle \Psi _{nlm}=\left({\frac {1}{2\pi }}\right)^{1/2}\cdot \left({\frac {2}{nr_{0}}}\right)^{1/2}\cdot \left({\frac {1}{2n\pi }}\right)^{1/2}\cdot }
⋅
[
(
n
−
l
+
1
)
!
[
(
n
+
1
)
!
]
3
]
1
/
2
⋅
[
2
l
+
1
2
⋅
l
−
|
m
|
!
l
+
|
m
|
!
]
1
/
2
⋅
P
l
m
(
cos
θ
)
e
i
m
ϕ
e
−
ρ
2
ρ
l
L
n
+
l
2
l
+
1
,
{\displaystyle \cdot \left[{\frac {(n-l+1)!}{[(n+1)!]^{3}}}\right]^{1/2}\cdot \left[{\frac {2l+1}{2}}\cdot {\frac {l-|m|!}{l+|m|!}}\right]^{1/2}\cdot P_{l}^{m}(\cos \theta )e^{im\phi }e^{-{\frac {\rho }{2}}}\rho ^{l}L_{n+l}^{2l+1},}
în care:
r
0
=
h
2
4
π
2
m
0
e
2
{\displaystyle r_{0}={\frac {h^{2}}{4\pi ^{2}m_{0}e^{2}}}}
reprezintă raza atomului de hidrogen în stare fundamentală, iar:
ρ
=
−
8
π
2
m
0
E
h
2
{\displaystyle \rho ={\sqrt {-{\frac {8\pi ^{2}m_{0}E}{h^{2}}}}}}
L
n
+
l
2
l
+
1
{\displaystyle L_{n+l}^{2l+1}}
polinoamele generalizate Laguerre .Pl m (cos θ) sunt funcțiile sferice asociate de gradul l și de ordinul m , iar n , l , m sunt numerele cuantice principal, azimutal, respectiv magnetic.
Soluțiile ecuației sunt compatibile cu realitatea fizică numai pentru anumite valori ale energiei E , numite valori proprii, egale cu:
E
n
=
−
m
0
Z
2
e
4
8
ϵ
0
2
n
2
h
2
,
{\displaystyle E_{n}=-{\frac {m_{0}Z^{2}e^{4}}{8\epsilon _{0}^{2}n^{2}h^{2}}},}
deci energia electronului este cuantificată.
Starea normală sau fundamentală a unui atom hidrogenoid corespunde valorilor n=1, l=0, m=0 ale numerelor cuantice.
Funcția de undă are valoarea proprie:
Ψ
100
=
1
(
π
r
0
3
)
1
/
2
⋅
e
−
r
r
0
{\displaystyle \Psi _{100}={\frac {1}{(\pi r_{0}^{3})^{1/2}}}\cdot e^{-{\frac {r}{r_{0}}}}}
și energia are valoarea:
E
1
=
−
m
0
Z
2
e
4
8
ϵ
0
2
h
2
.
{\displaystyle E_{1}=-{\frac {m_{0}Z^{2}e^{4}}{8\epsilon _{0}^{2}h^{2}}}.}





![{\displaystyle \cdot \left[{\frac {(n-l+1)!}{[(n+1)!]^{3}}}\right]^{1/2}\cdot \left[{\frac {2l+1}{2}}\cdot {\frac {l-|m|!}{l+|m|!}}\right]^{1/2}\cdot P_{l}^{m}(\cos \theta )e^{im\phi }e^{-{\frac {\rho }{2}}}\rho ^{l}L_{n+l}^{2l+1},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4b1db1cf82e80a004333ca7b0ffc9ecbe7e9c674)





