În matematică , polinoamele Laguerre , numite astfel în cinstea lui Edmond Laguerre (1834 - 1886), sunt soluțiile canonice ale ecuației Laguerre :
x
y
″
+
(
1
−
x
)
y
′
+
n
y
=
0
{\displaystyle x\,y''+(1-x)\,y'+n\,y=0\,}
care este o ecuație diferențială liniară de ordinul al doilea.
Această ecuație diferențială are soluții nesingulare numai dacă n este un întreg nenegativ.
Aceste polinoame, notate de regulă cu
L
0
,
L
1
,
…
{\displaystyle L_{0},L_{1},\dots }
șir polinomial ce poate fi definit prin formula Rodrigues
L
n
(
x
)
=
e
x
n
!
d
n
d
x
n
(
e
−
x
x
n
)
.
{\displaystyle L_{n}(x)={\frac {e^{x}}{n!}}{\frac {d^{n}}{dx^{n}}}\left(e^{-x}x^{n}\right).}
Ele sunt ortogonale unul pe celălalt în raport cu produsul scalar dat de
⟨
f
,
g
⟩
=
∫
0
∞
f
(
x
)
g
(
x
)
e
−
x
d
x
.
{\displaystyle \langle f,g\rangle =\int _{0}^{\infty }f(x)g(x)e^{-x}\,dx.}
Șirul polinoamelor Laguerre este un șir Sheffer .
Polinoamele Laguerre apar în mecanica cuantică, în partea radială a soluției ecuației Schrödinger pentru atomul cu un electron.
Fizicienii folosesc adesea o definiție a polinoamelor Laguerre mai mare cu un factor de
(
n
!
)
{\displaystyle (n!)}
Acestea sunt primele polinoame Laguerre:
n
L
n
(
x
)
{\displaystyle L_{n}(x)\,}
0
1
{\displaystyle 1\,}
1
−
x
+
1
{\displaystyle -x+1\,}
2
1
2
(
x
2
−
4
x
+
2
)
{\displaystyle {\scriptstyle {\frac {1}{2}}}(x^{2}-4x+2)\,}
3
1
6
(
−
x
3
+
9
x
2
−
18
x
+
6
)
{\displaystyle {\scriptstyle {\frac {1}{6}}}(-x^{3}+9x^{2}-18x+6)\,}
4
1
24
(
x
4
−
16
x
3
+
72
x
2
−
96
x
+
24
)
{\displaystyle {\scriptstyle {\frac {1}{24}}}(x^{4}-16x^{3}+72x^{2}-96x+24)\,}
5
1
120
(
−
x
5
+
25
x
4
−
200
x
3
+
600
x
2
−
600
x
+
120
)
{\displaystyle {\scriptstyle {\frac {1}{120}}}(-x^{5}+25x^{4}-200x^{3}+600x^{2}-600x+120)\,}
6
1
720
(
x
6
−
36
x
5
+
450
x
4
−
2400
x
3
+
5400
x
2
−
4320
x
+
720
)
{\displaystyle {\scriptstyle {\frac {1}{720}}}(x^{6}-36x^{5}+450x^{4}-2400x^{3}+5400x^{2}-4320x+720)\,}
Primele şase polinoame Laguerre Aceste polinoame pot fi exprimate sub formă de integrală pe contur
L
n
(
x
)
=
1
2
π
i
∮
e
−
x
t
/
(
1
−
t
)
(
1
−
t
)
t
n
+
1
d
t
{\displaystyle L_{n}(x)={\frac {1}{2\pi i}}\oint {\frac {e^{-xt/(1-t)}}{(1-t)\,t^{n+1}}}\;dt}
unde conturul este unul închis, ce ocolește originea în sens trigonometric.
Polinoamele Laguerre se pot defini recursiv, exprimând primele două polinoame ca
L
0
(
x
)
=
1
{\displaystyle L_{0}(x)=1\,}
L
1
(
x
)
=
1
−
x
{\displaystyle L_{1}(x)=1-x\,}
și apoi folosind relația de recurență pentru orice
k
≥
1
{\displaystyle k\geq 1}
L
k
+
1
(
x
)
=
1
k
+
1
(
(
2
k
+
1
−
x
)
L
k
(
x
)
−
k
L
k
−
1
(
x
)
)
{\displaystyle L_{k+1}(x)={\frac {1}{k+1}}{\bigg (}(2k+1-x)L_{k}(x)-kL_{k-1}(x){\bigg )}}
Proprietatea de ortogonalitate enunțată mai sus este echivalentă cu a spune dă dacă X este o variabilă aleatoare cu distribuție exponențială cu funcția de densitate de probabilitate
f
(
x
)
=
{
e
−
x
if
x
>
0
,
0
if
x
<
0
,
{\displaystyle f(x)=\left\{{\begin{matrix}e^{-x}&{\mbox{if}}\ x>0,\\0&{\mbox{if}}\ x<0,\end{matrix}}\right.}
atunci
E
(
L
n
(
X
)
L
m
(
X
)
)
=
0
dc.
n
≠
m
.
{\displaystyle E(L_{n}(X)L_{m}(X))=0\ {\mbox{dc.}}\ n\neq m.}
Distribuția exponențială nu este singura distribuție gamma . Un șir de polinoame ortogonale în raport cu distribuția gamma a căror funcție de densitate de probabilitate este, pentru
α
>
−
1
{\displaystyle \alpha >-1}
f
(
x
)
=
{
x
α
e
−
x
/
Γ
(
1
+
α
)
if
x
>
0
,
0
if
x
<
0
,
{\displaystyle f(x)=\left\{{\begin{matrix}x^{\alpha }e^{-x}/\Gamma (1+\alpha )&{\mbox{if}}\ x>0,\\0&{\mbox{if}}\ x<0,\end{matrix}}\right.}
este dat de rafinarea ecuației Rodrigues pentru polinoamele Laguerre generalizate :
L
n
(
α
)
(
x
)
=
x
−
α
e
x
n
!
d
n
d
x
n
(
e
−
x
x
n
+
α
)
.
{\displaystyle L_{n}^{(\alpha )}(x)={x^{-\alpha }e^{x} \over n!}{d^{n} \over dx^{n}}\left(e^{-x}x^{n+\alpha }\right).}
Acestea sunt uneori numite polinoame asociate Laguerre . Polinoamele Laguerre simple sunt recuperate din cele generalizate punând
α
=
0
{\displaystyle \alpha =0}
L
n
(
0
)
(
x
)
=
L
n
(
x
)
.
{\displaystyle L_{n}^{(0)}(x)=L_{n}(x).}
Polinoamele asociate Laguerre sunt ortogonale peste
[
0
,
∞
)
{\displaystyle [0,\infty )}
x
α
e
−
x
{\displaystyle x^{\alpha }e^{-x}}
∫
0
∞
e
−
x
x
α
L
n
(
α
)
(
x
)
L
m
(
α
)
(
x
)
d
x
=
Γ
(
n
+
α
+
1
)
n
!
δ
n
m
.
{\displaystyle \int _{0}^{\infty }e^{-x}x^{\alpha }L_{n}^{(\alpha )}(x)L_{m}^{(\alpha )}(x)dx={\frac {\Gamma (n+\alpha +1)}{n!}}\delta _{nm}.}
Următoarea integrală este necesară pentru tratarea atomului de hidrogen în mecanica cuantică ,
∫
0
∞
e
−
x
x
α
+
1
[
L
n
(
α
)
]
2
d
x
=
(
n
+
α
)
!
n
!
(
2
n
+
α
+
1
)
.
{\displaystyle \int _{0}^{\infty }e^{-x}x^{\alpha +1}\left[L_{n}^{(\alpha )}\right]^{2}dx={\frac {(n+\alpha )!}{n!}}(2n+\alpha +1).}
Polinoamele asociate Laguerre se supun următoarei ecuații diferențiale:
x
L
n
(
α
)
′
′
(
x
)
+
(
α
+
1
−
x
)
L
n
(
α
)
′
(
x
)
+
n
L
n
(
α
)
(
x
)
=
0.
{\displaystyle xL_{n}^{(\alpha )\prime \prime }(x)+(\alpha +1-x)L_{n}^{(\alpha )\prime }(x)+nL_{n}^{(\alpha )}(x)=0.\,}
Ele respectă următoarea relație de recurență pentru
n
≥
1
{\displaystyle n\geq 1}
L
n
+
1
(
α
)
(
x
)
=
1
n
+
1
(
(
2
n
+
1
+
α
−
x
)
L
n
(
α
)
(
x
)
−
(
n
+
α
)
L
n
−
1
(
α
)
(
x
)
)
.
{\displaystyle L_{n+1}^{(\alpha )}(x)={\frac {1}{n+1}}{\bigg (}(2n+1+\alpha -x)L_{n}^{(\alpha )}(x)-(n+\alpha )L_{n-1}^{(\alpha )}(x){\bigg )}.}
Două alte relații de recurență utile sunt
L
n
+
1
(
α
)
(
x
)
=
L
n
+
1
(
α
−
1
)
(
x
)
+
L
n
(
α
)
(
x
)
,
{\displaystyle L_{n+1}^{(\alpha )}(x)=L_{n+1}^{(\alpha -1)}(x)+L_{n}^{(\alpha )}(x),}
L
n
+
1
(
α
)
(
x
)
=
1
n
+
1
(
(
n
+
1
+
α
)
L
n
(
α
)
(
x
)
−
x
L
n
(
α
+
1
)
(
x
)
)
.
{\displaystyle L_{n+1}^{(\alpha )}(x)={\frac {1}{n+1}}{\bigg (}(n+1+\alpha )L_{n}^{(\alpha )}(x)-xL_{n}^{(\alpha +1)}(x){\bigg )}.}
Polinomul Laguerre generalizat de gradul
n
{\displaystyle n}
teoremei lui Leibnitz pentru derivarea produsului asupra formulei Rodrigues)
L
n
(
α
)
(
x
)
=
∑
m
=
0
n
(
n
+
α
n
−
m
)
(
−
x
)
m
m
!
{\displaystyle L_{n}^{(\alpha )}(x)=\sum _{m=0}^{n}{n+\alpha \choose n-m}{\frac {(-x)^{m}}{m!}}}
de unde se observă că coeficientul termenului dominant este
(
−
1
)
n
/
n
!
{\displaystyle (-1)^{n}/n!}
(
n
+
α
n
)
.
{\displaystyle {n+\alpha \choose n}.}
Primele polinoame Laguerre generalizate sunt:
L
0
(
α
)
(
x
)
=
1
{\displaystyle L_{0}^{(\alpha )}(x)=1}
L
1
(
α
)
(
x
)
=
−
x
+
α
+
1
{\displaystyle L_{1}^{(\alpha )}(x)=-x+\alpha +1}
L
2
(
α
)
(
x
)
=
x
2
2
−
(
α
+
2
)
x
+
(
α
+
2
)
(
α
+
1
)
2
{\displaystyle L_{2}^{(\alpha )}(x)={\frac {x^{2}}{2}}-(\alpha +2)x+{\frac {(\alpha +2)(\alpha +1)}{2}}}
L
3
(
α
)
(
x
)
=
−
x
3
6
+
(
α
+
3
)
x
2
2
−
(
α
+
2
)
(
α
+
3
)
x
2
+
(
α
+
1
)
(
α
+
2
)
(
α
+
3
)
6
{\displaystyle L_{3}^{(\alpha )}(x)={\frac {-x^{3}}{6}}+{\frac {(\alpha +3)x^{2}}{2}}-{\frac {(\alpha +2)(\alpha +3)x}{2}}+{\frac {(\alpha +1)(\alpha +2)(\alpha +3)}{6}}}
Derivarea de
k
{\displaystyle k}
d
k
d
x
k
L
n
(
α
)
(
x
)
=
(
−
1
)
k
L
n
−
k
(
α
+
k
)
(
x
)
.
{\displaystyle {\frac {\mathrm {d} ^{k}}{\mathrm {d} x^{k}}}L_{n}^{(\alpha )}(x)=(-1)^{k}L_{n-k}^{(\alpha +k)}(x)\,.}
Polinoamele Laguerre generalizate sunt legate de polinoamele Hermite :
H
2
n
(
x
)
=
(
−
1
)
n
2
2
n
n
!
L
n
(
−
1
/
2
)
(
x
2
)
{\displaystyle H_{2n}(x)=(-1)^{n}\ 2^{2n}\ n!\ L_{n}^{(-1/2)}(x^{2})}
și
H
2
n
+
1
(
x
)
=
(
−
1
)
n
2
2
n
+
1
n
!
x
L
n
(
1
/
2
)
(
x
2
)
{\displaystyle H_{2n+1}(x)=(-1)^{n}\ 2^{2n+1}\ n!\ x\ L_{n}^{(1/2)}(x^{2})}
unde
H
n
(
x
)
{\displaystyle H_{n}(x)}
polinoamele Hermite bazate pe funcția pondere
exp
(
−
x
2
)
{\displaystyle \exp {(-x^{2})}}
Din acest motiv, polinoamele Laguerre generalizate apar în tratamentul oscilatorului cuantic armonic .
Polinoamele Laguerre pot fi definite în termeni de funcții hipergeometrice , anume de funcții hipergeometrice confluente , ca
L
n
(
α
)
(
x
)
=
(
n
+
α
n
)
M
(
−
n
,
α
+
1
,
x
)
=
(
α
+
1
)
n
n
!
1
F
1
(
−
n
,
α
+
1
,
x
)
{\displaystyle L_{n}^{(\alpha )}(x)={n+\alpha \choose n}M(-n,\alpha +1,x)={\frac {(\alpha +1)_{n}}{n!}}\,_{1}F_{1}(-n,\alpha +1,x)}
unde
(
a
)
n
{\displaystyle (a)_{n}}
simbolul Pochhammer (care în acest caz reprezintă factorialul crescător ).
Eric W. Weisstein, „Laguerre Polynomial ”, de la MathWorld--A Wolfram Web Resource.
George Arfken și Hans Weber (2000 ). Mathematical Methods for Physicists . Academic Press. ISBN 0-12-059825-6 . 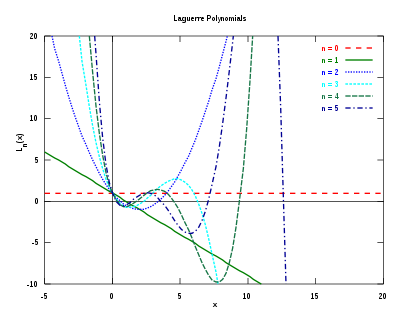





























![{\displaystyle \int _{0}^{\infty }e^{-x}x^{\alpha +1}\left[L_{n}^{(\alpha )}\right]^{2}dx={\frac {(n+\alpha )!}{n!}}(2n+\alpha +1).}](https://wikimedia.org/api/rest_v1/media/math/render/svg/747c49b8cb2c78abbad8f135bf0b6e391c792687)




















