Legea conservării energiei
| Acest articol are nevoie de ajutorul dumneavoastră. Puteți contribui la dezvoltarea și îmbunătățirea lui apăsând butonul Modificare. |
| Deși acest articol conține o listă de referințe bibliografice, sursele sale rămân neclare deoarece îi lipsesc notele de subsol. Puteți ajuta introducând citări mai precise ale surselor. |

Legea conservării energiei afirmă că energia totală a unui sistem fizic izolat rămâne nemodificată în timp, indiferent de natura proceselor interne ce au loc în sistem.
Cu alte cuvinte, diversele forme de energie ale unui sistem se pot transforma reciproc, dar suma cantităților tuturor formelor de energie rămâne constantă, ea nu poate fi creată sau distrusă. Potrivit concepțiilor fizicii moderne, orice cantitate de energie exprimă în același timp o masă, și reciproc oricărei mase îi corespunde o energie. Conservarea energiei, în fizica modernă, este echivalentă cu principiul conservării masei.
Legea conservării energiei este una din cele mai importante legi ale naturii, ea având implicații majore în toate domeniile științei și tehnicii. În activitățile cotidiene, dintre toate legile de conservare, această lege are cea mai însemnată implicare practică. Motivul primordial al acestei implicații constă în aceea că societatea este direct dependentă de efectuarea de lucru mecanic, definit într-o primă aproximație ca produsul dintre forță și deplasare, ceea ce se relizează prin consum de energie. Toate activitățile, începând cu viața de zi cu zi a oamenilor până la cele mai complexe procese industriale sau ale schimbului informațional, de exemplu, sunt dependente de capacitatea de a consuma energie. Legea conservării energiei este o expresie a acestei capacități, ea exclude, din principiu, existența unui perpetuum mobile de speța întâia, adică posibilitatea construirii unui agregat care ar produce mai multă energie decât primește din exterior.
Legea conservării energiei este o consecință a simetriei legilor fizicii la transformările liniare ale timpului, cu alte cuvinte, exprimă invarianța legilor odată cu trecera timpului.
Primul principiu al termodinamicii reprezintă legea conservării energiei pentru sistemele termodinamice.
De exemplu, atunci când folosim energie de orice fel și spunem într-un mod oarecum impropriu că o "consumăm", de fapt nu facem decât să asistam la trecerea (transformarea) energiei dintr-o forma în alta formă. De exemplu, energia potențială a unui pendul aflat în mișcare oscilatorie se transformă în energie cinetică, și invers.
Legile conservării reprezintă noțiuni fundamentale ale fizicii, ale teoriei relativității și mecanicii cuantice.
Evoluția istorică a conceptului[modificare | modificare sursă]

Legea conservării energiei în teoria căldurii[modificare | modificare sursă]
Principiul I al termodinamicii[modificare | modificare sursă]
Enunțul I[modificare | modificare sursă]
Variația energiei interne a unui sistem termodinamic, la trecerea lui dintr-o stare inițială dată, într-o stare finală dată, nu depinde de stările intermediare prin care trece sistemul, ci numai de stările inițială și finală: ΔU = U2 – U1.
Enunțul al II-lea[modificare | modificare sursă]
Variația energiei interne a unui sistem termodinamic, ΔU, la trecerea acestuia dintr-o stare inițială dată într-o stare finală, este egală cu suma dintre schimbul de căldură cu mediul exterior, Q1–2, și lucrul mecanic al forțelor exterioare care acționează asupra sistemului: ΔU = Q1–2 + Le.
Legea conservării energiei în mecanică[modificare | modificare sursă]
Conservarea energiei în mecanică este exprimată de regulă pentru sisteme pur mecanice, adică pentru sisteme supuse unor procese ce nu implică fenomene termice sau radiative, în particular, pentru punctul material sau sistemul de puncte materiale supuse legăturilor scleronome . Modelul dinamic pentru descrierea unor clase largi de procese mecanice care nu prezintă aspecte disipative este cel al unor sisteme supuse unui câmp de forțe conservative.
Sisteme conservative[modificare | modificare sursă]
În cazul mecanicii clasice, legea conservării energiei mecanice se enunță sub forma:
| În cazul în care caracteristicile mișcării mecanice a unui sistem sunt determinate doar de prezența unor forțe conservative, energia mecanică totală este o constantă a mișcării
sau: unde:
|
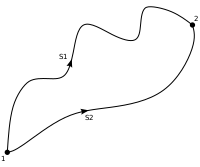
O forță conservativă, prin definiție, este dependentă doar de distanța dintre corpul studiat și un alt corp din vecinătatea lui. Lucrul mecanic al unei forțe conservative este independent de forma traiectoriei, el fiind funcție doar de poziția punctelor între care are loc deplasarea.
Legea conservării energiei mecanice nu se respectă decât în cazul sistemelor conservative. Când caracteristicile mișcării sunt determinate de alte tipuri de forțe, se vorbește despre legea conservării energiei în sens general, incluzându-se și efectele disipative, radiative etc.
Forțele conservative (câmpul vectorial al forțelor conservative ) derivă dintr-un potențial scalar , o funcție care depinde explicit numai de vectorul de poziție al puncului de aplicație al forței (poziția în care se calculează forța), față de originea sistemului de referință (ales convențional în punctul de potențial nul). În mecanica teoretică se demonstrează că relația dintre forța conservativă și potențialul său este dată de formula:
Lucrul mecanic este definit prin integrala temporală a produsului scalar dintre vectorul forță și vectorul viteză , integrarea se face între limitele t1 și t2, adică momentele de timp corespunzătoare pozițiilor inițială și finală.
Integrandul reprezintă valoarea negativă a derivatei temporale totale a potențialului , ceea ce se scrie analitic sub următoarea formă:
Astfel, teorema enunțată mai sus este demonstrată prin
Teorema lui Emmy Noether[modificare | modificare sursă]
Aceasta teoremă stabilește conexiunea dintre simetria, la aplicarea grupului transformărilor liniare ale timpului, și legile de conservare.
Conservarea energiei în teoria relativității[modificare | modificare sursă]
Legea conservării energiei în electrodinamică[modificare | modificare sursă]
Conservarea energiei și energia nucleară[modificare | modificare sursă]
Legătura nucleară și defectul de masă[modificare | modificare sursă]
Principii de conservare în reacții nucleare[modificare | modificare sursă]
Note[modificare | modificare sursă]
Bibliografie[modificare | modificare sursă]
- Iacob, Caius: Mecanică teoretică, Editura Științifică și Pedagogică, București, 1980
- Răduleț, R. și colab. Lexiconul Tehnic Român, Editura Tehnică, București, 1957-1966.
- Luca, D., Stan C. : Mecanica fizică, Editura Tehnopres, Iași, 2004.
























