Torsiune (mecanică)

Torsiunea unei bare cu secțiune pătrată

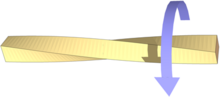
În mecanica solidului și rezistența materialelor torsiunea este răsucirea unui obiect datorită unui moment aplicat. Torsiunea este exprimată în pascali (Pa), newtoni pe metru pătrat sau multiplii acestora, în timp ce momentul este exprimat în newton metri (N•m). În secțiunile perpendiculare pe axa momentului tensiunea tangențială rezultată acționează într-un plan perpendicular pe axă.

În secțiunile transversale circulare, secțiunile rămân plane, torsiunea fiind însoțită doar de o deformație numită [unghi de] răsucire specifică, $\varphi .$ În secțiunile transversale necirculare, în afara răsucirii specifice apar și deformații axiale. Deoarece diferitele puncte ale secțiunii se deplasează axial în mod diferit, secțiunile transversale inițiale nu mai rămân plane. Ca urmare ipoteza lui Bernoulli privind conservarea planeității secțiunii nu se mai verifică. Pentru arbori cu secțiuni transversale uniforme care nu sunt supuse altor constrângeri momentul de torsiune este:

$M_{t}={\frac {I_{s}}{r}}\tau ={\frac {I_{s}}{\ell }}G\varphi$

unde:

M_t este momentul de torsiune aplicat, în Nm.

$\tau$ (tau) este tensiunea tangențială maximă pe suprafața exterioară

I_s este constanta de torsiune a secțiunii. Pentru bare rotunde sau țevi cu grosimea peretelui constantă, constanta de torsiune este chiar momentul de inerție polar al secțiunii, I_p, care moment de inerție polar este relativ mare și are o expresie simplă. Dar pentru alte forme, constanta de torsiune poate fi mult mai mică, iar calculul său poate fi complicat. Pentru acuratețe, cea mai bună metodă este analiza cu elemente finite (FEA). Altă metodă poate fi analogia cu membrana.

r este distanța dintre axă și cel mai îndepărtat punct al secținii de axă.

ℓ este lungimea obiectului în direcția axei momentului aplicat.

φ este unghiul de răsucire specifică în radiani.

G este modulul de elasticitate transversal, dat de obicei în MPa (megapascali) sau în N/mm².

Produsul GI_s este numit [modul de] rigiditate la răsucire.

Proprietăți

Rotorul unei turbine cu abur, la care arborele este lustruit pentru a evita fisurile de la suprafața lui

Tensiunea tangențială într-un punct al unui arbore este:

$\tau _{\varphi _{z}}={\frac {M_{t}r}{I_{p}}}.$

De observat că cea mai mare tensiune apare la suprafața arborelui, unde raza este maximă. Deoarece micile defecte ale suprafeței sunt concentratori de tensiuni, suprafața arborelui se lustruiește, pentru a reduce tensiunile și a prelungi durata de funcționare a arborelui.

Unghiul de răsucire este:

$\varphi ={\frac {M_{t}\ell }{GI_{p}}}.$

Ruperea la răsucire

Flambarea la torsiune a zonei dinaintea aripilor unui B-52. Se observă striațiile la 45°.

Tensiunile tangențiale principale din arbore pot fi analizate cu ajutorul cercului lui Mohr^⁠(d). Dacă arborele este încărcat numai prin torsiune, atunci una dintre tensiunile principale va fi de întindere, iar cealaltă de comprimare. Aceste tensiuni sunt orientate la un unghi elicoidal de 45° în jurul arborelui. Dacă arborele este realizat dintr-un material casant, atunci ruperea arborelui va fi determinată de o fisură inițiată de la suprafață și care se propagă până la miezul arborelui, ruptura avînd o formă elicoidală cu unghi de 45°.

În cazul arborilor tubulari cu pereți subțiri, cedarea se face la flambaj^⁠(d) prin răsucire, cu încrețituri formate la 45° față de axa arborelui.

Bibliografie

• Gheorghe Buzdugan, Rezistența materialelor, Ed. a IX-a revizuită, București: Editura Tehnică, 1970
• Indira Andreescu, Ștefan Mocanu, Compendiu de Rezistența Materialelor, (Universitatea Tehnică de Construcții din București), Editura Matrixrom, 2005, ISBN: 973-685-869-3
• Mircea Radeș, Rezistența materialelor I (curs Universitatea Politehnica din București), Editura Printech, 2010
• Mihai Hlușcu, Pavel Tripa, Rezistența materialelor, Vol. I Arhivat în 3 februarie 2024, la Wayback Machine. (curs Universitatea Politehnica Timișoara), Editura Mirton, 2014, ISBN: 978-973-521475-3