Accelerație liniară

fig.1 Acceleraţia unui mobil (punct material în mişcare) este raportul dintre variaţia vectorului viteză $\scriptstyle\Delta \vec v$ şi intervalul de timp $\scriptstyle\Delta t$ în care se produce această variaţie. Acest raport reprezintă vectorul acceleraţie medie corespunzător intervalului de timp şi el este răspunzător de variaţia atât a valorii cât şi a direcţiei vectorului viteză ce are loc în acel interval de timp. Pentru găsirea valorii instantanee la momentul t este necesară trecerea raportului la limită când $\scriptstyle\Delta t$ → 0, rezultatul este derivata temporală de ordinul întâi a vectorului viteză şi este un vector care nu e tangent la traiectoria mişcării.

fig.2 Componentele normale ale aceeleraţiei unei mişcări curbilinii plane Vectorul acceleraţie momentană este legat de punctul material aflat în mişcare pe o traiectorie oarecare (în general curbiline) şi este orientat spre interiorul curbei. Vectorul se poate descompune în două componente normale, numite şi componentele intrinseci după direcţia vectorului viteză, adică tangenta la traiectorie în punctul în care se află mobilul şi pe direcţia perpendiculară pe aceasta. Componenta tangenţială, $\scriptstyle \vec a_t$ are acelaşi suport ca şi vectorul viteză momentană, el produce variaţia valorii vitezei; compnenta normală, $\scriptstyle \vec a_c$, numită şi acceleraţie centripetă are direcţia razei de curbură locală a traiectoriei fiind orientată spre centrul de curbură, el are ca efect modificarea direcţiei vectorului viteză. În timpul mişcării, la orice moment de timp cele două componente sunt perpendiculare una pe cealaltă, putând să se modifice modulul lor.

Accelerația liniară sau uzual: accelerație, notată de regulă prin simbolul $\scriptstyle \vec a$, este în fizică o mărime vectorială care reprezintă variația vectorului viteză liniară în unitatea de timp.

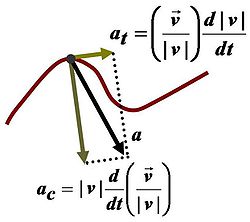
Este un vector legat, având punctul de aplicație în punctul material considerat. Ea are o componentă tangențială $\scriptstyle\vec a_t$, numită accelerația tangențială și o componentă normală $\scriptstyle\vec a_c$, numită accelerația centripetă. Mărimea fizică accelerație apare ca parametru al mișccării în ecuațiile diverselor tipuri de mișcări din cadrul cinematicii, dar și în expresia forței scrisă după legea a II-a a lui Newton.În cazul unei mișcări în care are loc scădera valorii vitezei, pentru accelerație se folosește denumirea alternativă de decelerație, uneori întârziere (expresie învechită).

Accelerația se măsoară în SI în $\scriptstyle\frac {m}{s^{2}}$ (metru pe secundă la pătrat). În sistemul de unități de măsură CGS unitatea de măsură pentru accelerație este $\scriptstyle\frac {cm}{s^{2}}$ (centimetru pe secundă la pătrat), cunoscută și sub numele gal și folosită de exemplu în seismometrie. În unele aplicații accelerația se exprimă în raport cu accelerația gravitațională, g.

În mecanică se utilizează noțiunea de vectorul accelerație medie definită ca raportul dintre variația vectorului viteză și intervalul de timp în care se produce variația:

$\vec a_m= \frac {\vec v_2-\vec v_1} {t_2-t_1}= \frac { \Delta \vec v} {\Delta t}$

Unde: $\scriptstyle \vec a_m$ este vectorul accelerație medie,$\scriptstyle \vec v_1$ și $\scriptstyle \vec v_2$ sunt vectorii viteză inițială și finală, $\scriptstyle t_1$ și $\scriptstyle t_2$ sunt momentele inițială și finală, $\scriptstyle \Delta \vec v=\vec v_2 - \vec v_1$ reprezintă vectorul variației vitezei, $\scriptstyle \Delta t=t_2 - t_1$ intervalul de timp dintre cele două momente.

Pentru descrierea exactă a mișcării se utilizează vectorul accelerație instantanee sau momentane care reprezintă vectorul accelerației pentru un moment dat. Aceasta se definește ca limita finită la care tinde raportul dintre variația vectorului viteză și intervalul de timp, atunci când valoarea intervalului de timp tinde la zero, ceea ce corespunde derivatei de ordinul întâi în raport cu timpul a vectorului viteză:

$\vec a=\lim_{\Delta t \to 0} \frac { \Delta \vec v} {\Delta t}= \frac{d \vec v}{dt}=\dot \vec v$

Țininând cont de faptul că vectorul viteză este la rândul său derivata de ordinul întâi a vectorului de poziție în raport cu timpul: $\scriptstyle \vec v= \frac{d \vec r}{dt}$, prin înlocuirea acestei relații în formula de mai sus, se găsește că vectorul accelerație instantanee este derivata de ordinul doi a vectorului de poziție în raport cu timpul:

$\vec a= \frac {d \vec v}{dt}=\frac {d}{dt} \left (\frac {d \vec r}{dt}\right)= \ddot \vec r$

Vectorul accelerație liniară, din punct de vedere matematic, este o funcție vectorială de o variabilă reală independentă: $\scriptstyle \vec a=\vec a(t)$. Relația funcțională dintre vectorii accelerație, viteză și de poziție se scrie sub forma:

$\vec a(t)=\dot \vec v(t)=\ddot \vec r(t)$

Noțiunea de accelerație

În mecanica clasică, starea de repaus relativ sau de mișcare rectilinie uniformă față de un sistem de referință inerțial sunt stări echivalente în acord cu legea întâi a mecanicii. Aceasta afirmă că un corp își păstrează una din aceste stări, atâta timp cât asupra lui nu acționează o forță externă. În cazul acțiunii unei forțe externe, starea dinamică a corpului față de un sistem de referință inerțial se modifică prin aceea că are loc modificarea în timp a vectorului viteză. Intensitatea modificării valorii și direcției vitezei trebuie raportat la valoarea intervalului de timp în care ele se produc. Pentru caracterizarea acestei intensități se introduce în studiul mișcărilor mecanice noțiunea de accelarație. Ea este intrinsec legată de forța care produce modificarea stării de mișcare prin legea a doua a mecanicii: $\scriptstyle \vec F=m \vec a$, unde $\scriptstyle\vec F$ este rezultanta forțelor externe, $\scriptstyle m$ este masa inertă a corpului (punctului material) și $\scriptstyle \vec a$ reprezintă accelerația corpului. Apariția accelerației, la un corp aflat în mișcare, este efectul acțiunii forței, pentru un corp de masă determinată, valoarea ei este direct proporțională cu forța și are aceeași direcție cu aceasta. Din punct de vedere cinematic, accelerația se definește pe baza efectului de modificare a vitezei și se introduce în studiul mișcării mecanice pe baza modelului punctului material aflat într-o mișcare oarecare. Denumirea de accelerație liniară este utilizată cu scopul de a o deosebi de accelerația unghiulară sau areolară. În limbaj comun prin folosirea expresiei accelerație, de regulă, se subânțelege mărimea accelerație liniară

fig. 3

vectorul accelerație liniară

Pentru definirea vectorului accelerație liniară, se consideră un punct material, aflat în mișcare pe o traiectorie oarecare, notă cu (C) în figura nr.3 din dreapta. Se consideră două momente diferite $\scriptstyle t_1= t$ și $\scriptstyle t_2 = t+ \Delta t$, numiți în continuare moment inițial și respectiv moment final, la care punctul material se află în punctul $\scriptstyle P$, respectiv $\scriptstyle Q$. La momentul inițial, vectorul de viteză al punctului material este $\scriptstyle \vec v_1= \vec v$ iar la momentul final $\scriptstyle\vec v_2= \vec v+\Delta \vec v$, numiți vector de viteză inițială și finală. Calculând variația vectorului viteză, produsă în intervalul de timp $\scriptstyle \Delta t$, se construiește vectorul $\scriptstyle \Delta \vec v=\vec v_2-\vec v_1$, prezentat în figura 3 dreapta, jos. Acest vector este o măsura a schimbării stării de mișcare atunci când punctul material s-a deplasat între cele două poziții. Pentru a caracteriza rata acestei schimbări este nevoie de raportarea lui la intervalul de timp în care se produce modificarea. Cu alte cuvinte, se calculează „viteza” de variație a vectorului viteză. Rezultatul raportării este vectorul accelerație liniară, corespunzător intervalului de timp $\scriptstyle \Delta t$.

accelerație medie

Raportul dintre variația vectorului viteză și intervalul de timp exprimă o accelerație medie și nu valoarea exactă a accelerației într-un moment de timp. În intervalul de timp în care are loc deplasarea punctului material între cele două puncte, vectorul viteză poate să se modifice în valoare și direcție în proporții diferite decât cel calculat pentru momentele final și inițial. Expresia vectorului accelerație liniară medie se scrie sub forma:

$\vec a_m= \frac {\vec v_2-\vec v_1} {t_2-t_1}= \frac { \Delta \vec v} {\Delta t}$

În figura 3. vectorul accelerație este notat prin simbolul $\scriptstyle < a >$. Valoarea acestui vector este proporțională cu valoarea variației vectorului vitezei și are direcția paralelă cu aceasta. Cunoașterea accelerației medii, permite cel mult, calcularea variației vitezei pentru intervalul de timp pentru care este dată, dar nu permite calculul exact al deplasării sau al drumului parcurs. Pentru descrierea exactă a stării cinematice pe tot parcursul mișcării, este nevoie de cunoașterea cu precizie a vectorului accelerației în orice moment, respectiv în oricare punct de pe traiectorie.

Vezi și

• Accelerație unghiulară
• Teorema lui Siacci

Bibliografie

Acest articol conține text din Dicționarul Enciclopedic Român 1962, aflat acum în domeniul public.