Teorema numerelor prime

Teorema numerelor prime descrie distribuția asimptotică a numerelor prime.

În linii mari, teorema precizează că, dacă N este un număr natural suficient de mare, probabilitatea ca un alt număr natural, din vecinătatea lui N să fie prim, este ${\frac {1}{ln\;N}}$ , unde ln N este logaritmul natural al lui N. De exemplu, dacă N=10 000, aproximativ unul din 9 sunt prime, iar dacă N=1.000.000.000, numai unul din 21 numere (din vecinătatea lui N) sunt prime.

Enunțul teoremei

Graficul comparaţiei dintre $\pi (x)$   şi   ${\frac {x}{\ln {x}}}$.

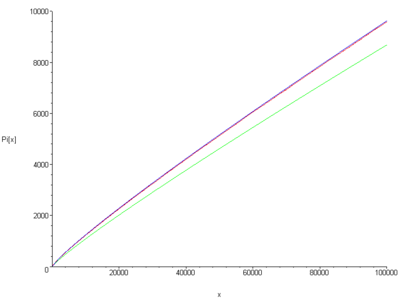
Se definește „funcția număr prim” $\pi$

$\pi (x)=\#\{p\in \mathbb {P} \mid p\leq x\}$ ,

unde $x\in \mathbb {R}$ iar $\mathbb {P}$ este mulțimea numerelor prime.

(Simbolul $\#M$ reprezintă numărul de elemente sau cardinalul mulțimii M. )

Așadar, $\pi (x)$ definește numărul numerelor prime mai mici decât x.

Teorema numerelor prime afirmă că:

$\lim _{x\to \infty }{\frac {\pi (x)}{\frac {x}{\ln(x)}}}=1$.

Sau, cu alte cuvinte, funcțiile $\pi (x)$ și ${\frac {x}{\ln(x)}}$ sunt asimptotic echivalente.

Istoric

Teorema numerelor prime demonstrată pentru prima dată de matematicianul francez Jacques Hadamard, în 1896. Teorema a fost demonstrată independent, în același an, și de Charles Jean de la Vallée-Poussin^{⁠(en)[traduceți]}.

Tabel cu π(x), x / ln x și Li(x)

x	π(x)	π(x) - x / lnx	Li(x) - π(x)	x / π(x)
10	4	-0,3	0,921	2,2	2,500
102	25	3,3	1,151	5,1	4,000
103	168	23	1,161	10	5,952
104	1.229	143	1,132	17	8,137
105	9.592	906	1,104	38	10,425
106	78.498	6.116	1,084	130	12,740
107	664.579	44.158	1,071	339	15,047
108	5.761.455	332.774	1,061	754	17,357
109	50.847.534	2.592.592	1,054	1.701	19,667
1010	455.052.511	20.758.029	1,048	3.104	21,975

Bibliografie

• Ingham, A.E. - The Distribution of Prime Numbers, Cambridge University, 1990
• Hardy, G.H. - An Introduction to the Theory of Numbers, Oxford University Press, Oxford, 1979

Legături externe

• Tabele cu numere prime Arhivat în 15 noiembrie 2010, la Wayback Machine. de Anton Felkel
• Teorema numerelor prime la MathWorld
• Prime Number Generator Arhivat în 4 septembrie 2009, la Wayback Machine.

Vezi și

• Indicatorul lui Euler