Transformările lui Lorentz

De la Wikipedia, enciclopedia liberă

Salt la: Navigare, căutare
 Acest articol sau această secţiune are bibliografia incompletă sau inexistentă.
Puteţi ajuta găsind susţinere bibliografică pentru conţinutul paginii.

În fizică, transformările Lorentz fac conversia între două măsurători diferite, efectuate de doi observatori diferiţi, asupra spaţiului şi timpului, atunci când un observator este în mişcare uniformă şi rectilinie în raport cu celălalt. În (relativitatea galileiană) din fizica clasică, singura conversie considerată necesară era x' = x − vt, descriind cum se deplasează originea sistemului de coordonate al unui observator prin spaţiu în raport cu a celuilalt, la viteza v de-a lungul axei x din fiecare sistem. Conform relativităţii restrânse, aceasta este doar o aproximaţie suficientă la viteze mici în raport cu cea a luminii, şi în general rezultatul este nu doar o deplasare de-a lungul coordonatelor x; vor fi distorsionate şi timpul şi spaţiul.

Dacă spaţiul ar fi omogen, atunci transformarea Lorentz este una liniară. De asemenea, deoarece teoria relativităţii postulează că viteza luminii este aceeaşi pentru toţi observatorii, trebuie să păstreze intervalul de spaţiu-timp dintre două evenimente din spaţiul Minkowski. Transformările Lorentz descriu doar transformările în care evenimentul de la x=0, t=0 este fix, astfel încât pot fi considerate rotaţii ale spaţiului Minkovski. Setul mai general de transformări care include şi translaţiile este cunoscut sub numele de grup Poincaré.

Henri Poincaré (1905) a denumit transformările Lorentz după fizicianul şi matematicianul olandez Hendrik Lorentz. Ele reprezintă fundamentul matematic a teoriei relativităţii restrânse a lui Albert Einstein. Transformările Lorentz elimină contradicţiile dintre teoriile electromagnetismului şi mecanicii clasice. Ele au fost deduse de către Joseph Larmor (1897) şi Lorentz (1899, 1904). În 1905, Einstein le-a dedus pe baza ipotezei covarianţei Lorentz şi a postulării constanţei vitezei luminii în orice sistem de referinţă inerţial.

Cuprins

[modifică] Transformările Lorentz pentru sisteme în configuraţie standard

Diagrama 1. Modificarea percepţiei spaţiu-timpului de-a lungul liniei de univers a unui observator care accelerează rapid.

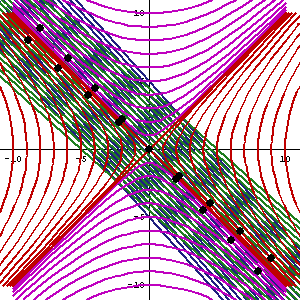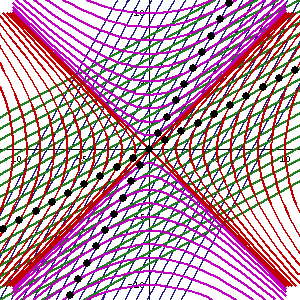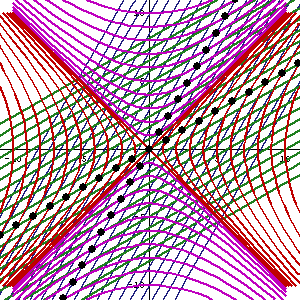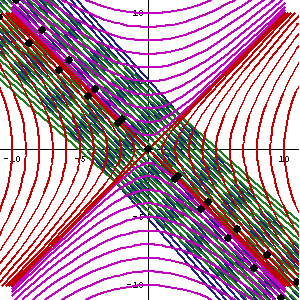
În această animaţie, direcţia verticală indică timpul iar cea orizontală indică distanţa, linia punctată este traiectoria spaţiu-timp ("linia de univers") a observatorului. Sfertul inferior al diagramei arată evenimentele vizibile pentru observator, iar sfertul superior arată conul de lumină- cei care pot vedea observatorul. Punctele mici sunt evenimente arbitrare din spaţiu-timp.

Panta liniei de univers (deviaţia de la verticală) dă viteza relativă faţă de observator. De observat cum percepţia spaţiu-timpului se modifică atunci când observatorul accelerează.

Presupunem că există doi observatori O şi Q, fiecare cu propriul lui sistem de coordonate cartezian pentru a măsura intervalele de timp şi spaţiu. O foloseşte (t,x,y,z) şi Q foloseşte (t',x',y',z'). Presupunem, mai departe, că sistemele de coordonate sunt orientate astfel încât axa x şi axa x' se suprapun, axa y este paralelă cu axa y' , şi la fel şi axa zcu axa z' . Viteza relativă a celor doi observatori este v de-a lungul axei comune x. Presupunem şi că originea celor două sisteme de coordonate that este aceeaşi. Dacă toate acestea sunt valabile, atunci se spune că aceste sisteme de coordonate sunt în configuraţie standard. O prezentare simetrică între transformarea Lorentz directă şi cea inversă se poate obţine dacă sistemele de coordonate sunt în configuraţie simetrică. Forma simetrică evidenţiază faptul că toate legile fizicii trebuie să fie de aşa natură încât ele rămân neschimbate sub o transformare Lorentz.

Transformarea Lorentz pentru sistemele în configuraţie standard este:

\begin{align}t' &= \gamma \left( t - \frac{v x}{c^{2}} \right) \\ x' &= \gamma \left( x - v t \right)\\ y' &= y \\ z' &= z \end{align}

unde \gamma = { 1 \over \sqrt{1 - \frac{v^2}{c^2}} }, se numeşte factor Lorentz.

[modifică] Forma matriceală

Această transformare Lorentz este adesea exprimată în formă matriceală astfel:

\begin{bmatrix} c t' \\ x' \\ y' \\ z' \end{bmatrix} = \begin{bmatrix} \gamma&-\beta \gamma&0&0\\ -\beta \gamma&\gamma&0&0\\ 0&0&1&0\\ 0&0&0&1\\ \end{bmatrix} \begin{bmatrix} c\,t \\ x \\ y \\ z \end{bmatrix}\ .

sau, mai general, pentru direcţiile x, y, şi z:

\begin{bmatrix} c\,t' \\ x' \\ y' \\ z' \end{bmatrix} = \begin{bmatrix} \gamma&-\beta_x\,\gamma&-\beta_y\,\gamma&-\beta_z\,\gamma\\ -\beta_x\,\gamma&1+(\gamma-1)\frac{\beta_{x}^{2}}{\beta^{2}}&(\gamma-1)\frac{\beta_{x}\beta_{y}}{\beta^{2}}&(\gamma-1)\frac{\beta_{x}\beta_{z}}{\beta^{2}}\\ -\beta_y\,\gamma&(\gamma-1)\frac{\beta_{y}\beta_{x}}{\beta^{2}}&1+(\gamma-1)\frac{\beta_{y}^{2}}{\beta^{2}}&(\gamma-1)\frac{\beta_{y}\beta_{z}}{\beta^{2}}\\ -\beta_z\,\gamma&(\gamma-1)\frac{\beta_{z}\beta_{x}}{\beta^{2}}&(\gamma-1)\frac{\beta_{z}\beta_{y}}{\beta^{2}}&1+(\gamma-1)\frac{\beta_{z}^{2}}{\beta^{2}}\\ \end{bmatrix} \begin{bmatrix} c\,t \\ x \\ y \\ z \end{bmatrix}\ .

unde \beta = \frac{v}{c}=\frac{\|\vec{v}\|}{c} şi \gamma = \frac{1}{\left( 1-\beta^2 \right)^\frac{1}{2}}.

[modifică] Rapiditatea

Transformarea Lorentz poate fi pusă într-o altă formă utilă introducând un parametru φ numit rapiditate (o instanţă de unghi hiperbolic) prin ecuaţia:

e^{\phi} = \gamma(1+\beta) = \gamma \left( 1 + \frac{v}{c} \right) = \sqrt \frac{1 + v/c}{1 - v/c}

Echivalent:

\phi = \ln \left[\gamma(1+\beta)\right] , -\phi = \ln \left[\gamma(1-\beta)\right] \,

Atunci transformarea Lorentz în configuraţie standard este:

c t-x = e^{- \phi}(c t' - x')\ ,
c t+x = e^{\phi}(c t' + x')\ ,
y = y'\ ,
z = z'\ .

[modifică] Expresii trigonometrice hiperbolice

Se poate arăta şi că:

\gamma = \cosh(\phi) = { e^{\phi} + e^{-\phi} \over 2 }
\beta = \tanh(\phi) = { e^{\phi} - e^{-\phi} \over e^{\phi} + e^{-\phi} }

şi deci,

\beta \gamma = \sinh(\phi) = { e^{\phi} - e^{-\phi} \over 2 }

[modifică] Rotaţii hiperbolice de coordonate

Substituind aceste expresii în forma matriceală a transformării, avem:

\begin{bmatrix} c t' \\ x' \\ y' \\ z' \end{bmatrix} = \begin{bmatrix} \cosh(\phi) &-\sinh(\phi)&0&0\\ -\sinh(\phi) & \cosh(\phi) &0&0\\ 0&0&1&0\\ 0&0&0&1\\ \end{bmatrix} \begin{bmatrix} c t \\ x \\ y \\ z \end{bmatrix}\ .

Astfel, transformarea Lorentz poate fi văzută ca o rotaţie hiperbolică de coordonate în spaţiul Minkowski, unde rapiditatea φ reprezintă unghiul hiperbolic de rotaţie.

Adus de la http://ro.wikipedia.org/wiki/Transform%C4%83rile_lui_Lorentz
Unelte personale