Săgeată (tehnică)

Săgeata ( f ) unei grinzi în urma încărcării

În tehnică săgeata ( f ) este deplasarea fibrei medii deformate a unui element constitutiv în urma deformării cauzate de încărcări. Prin extensie, termenul este folosit și pentru unghiurile ( φ ) tangentei la fibra medie deformată în această situație.^[1]

Săgeata poate fi calculată prin integrarea funcției care descrie matematic panta fibrei medii deformate sub acea sarcină.

Există formule standard pentru calculul săgeților configurațiilor comune de grinzi și a unor cazuri de încărcare, punctuală sau distribuită. Altfel, se folosesc metode precum lucrul mecanic virtual, integrarea analitică,^[2] metoda Castigliano,^[3] metoda lui Macaulay sau metoda rigidității directe. Deformarea elementelor grinzilor este de obicei calculată pe baza teoriei Euler–Bernoulli^⁠(d) în timp ce cea a unui element de placă sau carcasă este calculată utilizând teoria plăcilor^⁠(d).

Un exemplu de utilizare a săgeții în acest context este în construcția clădirilor. Adesea arhitecții și constructorii aleg materialele ținând cont de deformații.

Săgețile la diverse încărcări și moduri de sprijin

Grinzile pot varia foarte mult prin geometrie și materiale. De exemplu, o grindă poate fi dreaptă sau curbă. Poate avea o secțiune transversală constantă sau variabilă. Poate fi realizată în întregime din același material (omogen) sau poate fi formată din materiale diferite. Unele dintre aceste lucruri îngreunează analiza, dar multe aplicații inginerești implică cazuri care nu sunt atât de complicate. Analiza este simplificată dacă:

grinda este dreaptă și orice modificare a secțiunii este mică;
grinda este elastică, adică respectă Legea lui Hooke;
grinda este subțire (raportul dintre lungime și înălțimea secțiunii este mai mare de 10);
sunt luate în considerare numai săgețile mici (săgeta maximă este mai mică de 1/10 din deschidere).

În acest caz, relația care descrie fibra medie deformată a unei bare (grinzi) ( $w$ ) poate fi aproximată ca:

{\cfrac {\mathrm {d} ^{2}w(x)}{\mathrm {d} x^{2}}}={\frac {M(x)}{E(x)I(x)}}

unde derivata a doua a fibrei medii deformate în funcție de $x$ este interpretată drept curbura sa, $E$ este modulul lui Young, $I$ este momentul de inerție al secțiunii, iar $M$ este momentul încovoietor din bară.

Dacă bara are secțiune constantă, materialul din care este făcută este omogen și este încărcată cu o sarcină uniform distribuită $q$ , expresia de mai sus devine:

EI~{\cfrac {\mathrm {d} ^{4}w(x)}{\mathrm {d} x^{4}}}=q(x)

Această ecuație poate fi rezolvată pentru diverse tipuri de încărcări și condiții la limită. În continuare sunt prezentate o serie de exemple simple. Formulele rezultate sunt aproximări obținute pentru bare prismatice lungi, subțiri, omogene, cu deformări mici și proprietăți elastice liniare. În conformitate cu aceste restricții, aproximările ar trebui să dea rezultate în limita a 5 % din deformația efectivă.

În toate exemplele de mai jos:

$F$ este o forță concentrată, în [N] (alternativ, în [MN]);
$q$ este o sarcină uniform distribuită, în [N/m] (alternativ, în [MN/m]);
$L$ este lungimea barei, în [m];
$E$ este modulul lui Young, în [N/m²] (alternativ, în [MN/m²]). Deși unitatea de măsură N/m² are aceeași valoare ca și Pa, unitatea Pa se folosește la presiuni (externe), în timp ce în rezistența materialelor solicitările sunt tensiuni (interne).
$I$ este momentul de inerție axial (la încovoiere) al barei, în [m⁴];
$\delta$ este săgeata, în [m];
$\phi$ este unghiul tangentei la fibra medie deformată, în [radiani].

Unitățile care intră în relații trebuie să formeze un sistem de unități consistent. Actual se folosesc unitățile din SI. În decursul timpului în tehnică s-au folosit unitățile din sistemul MKfS. În țările de limbă anglo-saxonă se mai folosesc unitățile din sistemul anglo-saxon.

Grinzi în consolă

Schema deformării unei grinzi în consolă

Grinzile în consolă au un capăt fix, astfel încât unghiul și săgeata la acel capăt trebuie să fie zero.

Grindă în consolă încărcată la capăt

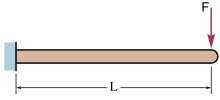
La bara în consolă (considerată fără greutate) încărcată cu o forță la capătul liber săgeata elastică și unghiul la capătul liber sunt:^[4]^[5]

\delta _{B}={\frac {FL^{3}}{3EI}}

\phi _{B}={\frac {FL^{2}}{2EI}}

De notat că dacă lungimea se dublează, săgeata crește de opt ori. Săgeata și unghiul în orice punct, $x$ , de-a lungul barei în consolă încărcată la capăt pot fi calculate cu relațiile:^[4]

\delta _{x}={\frac {Fx^{2}}{6EI}}(3L-x)

\phi _{x}={\frac {Fx}{2EI}}(2L-x)

Notă: La $x=L$ (capătul barei) ecuațiile pentru $\delta _{x}$ și $\phi _{x}$ devin identice cu cele pentru $\delta _{B}$ și $\phi _{B}$ de mai sus.

Grindă în consolă încărcată cu o sarcină uniform distribuită

La bara în consolă încărcată cu o sarcină distribuită (putând include greutatea ei) la capătul liber săgeata elastică și unghiul la capătul liber sunt:^[4]^[6]

\delta _{B}={\frac {qL^{4}}{8EI}}

\phi _{B}={\frac {qL^{3}}{6EI}}

Săgeata și unghiul într-un punct $x$ oarecare de-a lungul barei în consolă încărcată cu o sarcină uniform distribuită pot fi calculate cu relațiile:^[4]

\delta _{x}={\frac {qx^{2}}{24EI}}(6L^{2}-4Lx+x^{2})

\phi _{x}={\frac {qx}{6EI}}(3L^{2}-3Lx+x^{2})

Grinzi rezemate la capete

Schema deformării unei grinzi rezemate la capete

O grindă rezemată la capete permite rotația capetelor (deci unghiuri la capete) dar nu și săgeți la capete.

Grindă rezemată la capete încărcată cu o forță la mijloc

La bara rezemată la capete încărcată cu o forță la mijloc săgeata în orice punct, $x$ , poate fi calculată cu:^[4]

\delta _{x}={\frac {Fx}{48EI}}(3L^{2}-4x^{2})

pentru

0\leq x\leq {\frac {L}{2}}

În cazul particular în care forța este la mijlocul barei relația devine:^[4]^[7]

\delta _{C}={\frac {FL^{3}}{48EI}}

săgeata la mijloc fiind maximă.

Grindă rezemată la capete încărcată cu o forță într-un punct oarecare

În acest caz, săgeata se poate calcula cu relația:^[4]

\delta _{max}={\frac {Fa(L^{2}-a^{2})^{3/2}}{9{\sqrt {3}}LEI}}

unde $a$ este distanța de la punctul de aplicare al forței la cel mai apropiat reazem.

Distanța $x_{1}$ de cel mai apropiat reazem la care apare săgeata maximă este:^[4]

x_{1}={\sqrt {\frac {L^{2}-a^{2}}{3}}}

Grindă rezemată la capete încărcată cu o sarcină distribuită uniformă

La o bară rezemată la capete încărcată cu o sarcină distribuită uniformă săgeata maximă apare la mijlocul barei și poate fi calculată cu relația:^[4]^[8]

\delta _{C}={\frac {5qL^{4}}{384EI}}

Săgeata într-un punct $x$ oarecare poate fi calculată cu:^[4]

\delta _{x}={\frac {qx}{24EI}}(L^{3}-2Lx^{2}+x^{3})

Modificarea lungimii grinzii

Diferența de lungime între bara încărcată și cea neîncărcată (întotdeauna negativă) este în general mică. Dacă se cunoaște funcția care indică săgețile $\delta _{x}$ pentru orice $x$ , diferența de lungime poate fi calculată integrând fibra medie deformată $\theta _{x}$ pe lungime.

Unde:

\Delta L

este diferența de lungime

\theta _{x}

este funcția fibrei medii deformate (prima derivată a

\delta _{x}

)

\Delta L=-{\frac {1}{2}}\int _{0}^{L}(\theta (x))^{2}dx

^[9]

Dacă bara este uniformă și se cunosc săgețile, diferența se poate calcula fără a fi necesare alte date.

Utilizări

În special în construcții deformațiile sunt criterii pentru alegeri. De exemplu la o structură de oțel și sticlă deformațiile trebuie să fie mici pentru a nu sparge sticlele (există compensatoare, dar și ele au o plajă limitată de preluare a săgeților).

Note

^ Buzdugan, Rezistența…, p. 144
^ Buzdugan, Rezistența…, p. 146
^ Buzdugan, Rezistența…, pp. 300–305
^ ^a ^b ^c ^d ^e ^f ^g ^h ⁱ ^j en Gere, James M.; Goodno, Barry J. Mechanics of Materials (ed. Eighth). pp. 1083–1087. ISBN 978-1-111-57773-5.
^ Buzdugan, Rezistența…, p. 147
^ Buzdugan, Rezistența…, pp. 148–149
^ Buzdugan, Rezistența…, 1970, p. 154
^ Buzdugan, Rezistența…, pp. 149–150
^ Formulele Roark pentru tensiuni și deformații, Ed. a 8-a, ecuațiile 8.1–14

Bibliografie

Gheorghe Buzdugan, Rezistența materialelor, ed. a IX-a revizuită, București: Ed. Tehnică, 1970

Legături externe

en Deflection of beams
en Beam Deflections

[1] Buzdugan, Rezistența…, p. 144

[2] Buzdugan, Rezistența…, p. 146

[3] Buzdugan, Rezistența…, pp. 300–305

[gere-4] ^ ^a ^b ^c ^d ^e ^f ^g ^h ⁱ ^j en Gere, James M.; Goodno, Barry J. Mechanics of Materials (ed. Eighth). pp. 1083–1087. ISBN 978-1-111-57773-5.

[5] Buzdugan, Rezistența…, p. 147

[6] Buzdugan, Rezistența…, pp. 148–149

[7] Buzdugan, Rezistența…, 1970, p. 154

[8] Buzdugan, Rezistența…, pp. 149–150

[9] Formulele Roark pentru tensiuni și deformații, Ed. a 8-a, ecuațiile 8.1–14

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]