Capacitate electrică
În electricitate și electromagnetism, capacitatea electrică este o mărime fizică scalară care exprimă proprietatea corpurilor conductoare electric de a înmagazina și păstra sarcini electrice. Măsura ei se definește prin raportul dintre sarcina electrică a corpului izolat și potențialul său, exprimat față de un punct depărtat la infinit de potențial electric nul.[1]Capacitatea electrică este numeric egală cu sarcina electrică care produce o variație unitară a potențialului electric al unui conductor electric izolat. Unitatea de măsură în SI este faradul, notat prin litera F. Capacitatea electrică este principala caracteristică a dispozitivelor (elementelor de circuit electric) numite condensatoare.
Relația capacitate, sarcină, potențial[modificare | modificare sursă]
Capacitatea electrică (C) este direct proporțională față de sarcina electrică încărcată (Q), și invers proporțional față de tensiunea electrică (V):
Caz general[modificare | modificare sursă]

Pentru o configurație oarecare , a două corpuri conductoare separate de un mediu dielectric, capacitatea electrică a sistemului se calculează cu ajutorul formulei:
unde este vectorul inducție electrică iar reprezintă vectorul intensității câmpului electric.
Pentru vid, formula de mai sus devine:
- .
Formulă dimensională și unități de măsură[modificare | modificare sursă]
Conform analizei dimensionale, formula dimensională pentru capacitate se scrie sub forma:
Adică dimensiunea fizică a capacității electrice este masă la puterea minus unu ori lungime la minus doi ori timpul la puterea a patra ori intensitatea curentului electric la pătrat.
În Sistemul Internațional de Măsuri sarcina electrică se măsoară în coulomb, C și potențialul în volt, V, rezultă că unitatea de măsură pentru capacitatea electrică este:
În SI, capacitatea electrică se măsoară deci în farad, notat prin litera F, care este egal cu coulomb ori volt la puterea minus unu. Capacitatea electrică de un farad este numeric egală cu sarcina electrică de un coulomb, înmagazinată pe un corp conductor aflat la un potențial de un volt față de un punct la infinit de potențial nul.
Circuit paralel, circuit serie[modificare | modificare sursă]


Prin legarea în paralel (1.) a condensatoarelor se obține o capacitate (echivalentă), C, mai mare decât capacitățile individuale, iar prin legare în serie (2.) capacitatea echivalentă (totală) rezultată, este mai mică decât cea mai mică capacitate individuală a acestui circuit serie.
- (legarea în paralel).
- (legarea în serie).
Capacități electrice ale unor condensatoare și sisteme de conductoare[modificare | modificare sursă]
Dispozitivul cel mai simplu pentru a se încărca cu electricitate este condensatorul cu plăci conductoare paralele (plane). Un condensator de acest fel are (constructiv) capacitatea direct proporțională cu suprafața plăcilor conductoare și invers proporțională cu distanța dintre ele. Pentru o sarcină (încărcătură) electrică Q, în cazul unui condensator format din două armături plan-paralele, o armătură este încărcată cu sarcina electrică , iar cealaltă o sarcină negativă .
| Denumirea condensatorului | Formula capacității | Reprezentare schematică |
|---|---|---|
| Condensator plan | 
| |
| Cablu electric coaxial sau condensator cilindric de lungime |

| |
| Condensator sferic | 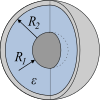
| |
| Sferă conductoare de rază față de punctul de la infinit | ||
| Cilindri paraleli de lungimi egale | 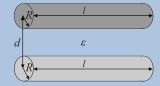
| |
| Conductor filiform de lungime , paralel cu o suprafață conductoare plană. |  d > R | |
| Două sfere conductoare de raze identice | d: distanța dintre centrele sferelor, d > 2a, D: d/2a, γ: constanta Euler-Mascheroni |
Legendă simboluri
- aria suprafeței armăturii
- distanța dintre armături
- lungimea armăturilor
- respectiv razele armăturilor
- permitivitatea electrică a dielectricului, unde este permitivitatea electrică a vidului și reprezintă permitivitatea relativă a dielectricului față de vid
- În reprezentarea schematică a diverșilor condensatori, armăturile sunt reprezentate prin culorile gri deschis respectiv gri închis, iar mediul dielectric prin albastru.
Note[modificare | modificare sursă]
- ^ Uneori, prin termenul de capacitate se denumește prescurtat dispozitivul în care capacitatea electrică este folosită ca proprietate principală a acestui dispozitiv, de exemplu condensatorul.
Vezi și[modificare | modificare sursă]
Bibliografie[modificare | modificare sursă]
- A. Amuzescu, D. Popovici Curs de electrotehnică Politehnica București Catedra de electrotehnică Editura Printech București 1999






![{\displaystyle [C]={\frac {[Q]}{[V]}}=M^{-1}\cdot L^{-2}\cdot T^{4}\cdot I^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/821315f07f929e0eefab6abbc1bdea8369b5ab17)
![{\displaystyle [C]_{SI}={\frac {[Q]_{SI}}{[V]_{SI}}}={\frac {C}{V}}=F(farad)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/88c063068690bd440a1b79c12cd80f265d2452dd)





















