Pavare apeirogonală de ordinul 3

Pavare apeirogonala de ordinul 3
Pe modelul discului Poincaré al planului hiperbolic
Descriere
Tip	pavare uniformă hiperbolică
Configurația vârfului	∞3
Configurația feței	V3∞
Simbol Wythoff	3 | ∞ 2 2 ∞ | ∞ ∞ ∞ ∞ |
Simbol Schläfli	{∞,3} t{∞,∞} t(∞,∞,∞)
Diagramă Coxeter
Grup de simetrie	[∞,3], (*∞32) [∞,∞], (*∞∞2) [(∞,∞,∞)], (*∞∞∞)
Grup de rotație	[∞,3]+, (∞32) [∞,∞]+, (∞∞2) [(∞,∞,∞)]+, (∞∞∞)
Poliedru dual	pavare triunghiulară de ordin infinit
Proprietăți	tranzitivă pe vârfuri, laturi și fețe

În geometrie pavarea apeirogonală de ordinul 3 este o pavare regulată a planului hiperbolic. Este reprezentată de simbolul Schläfli {∞,3}, având trei apeirogoane în jurul fiecărui vârf. Fiecare apeirogon este înscris într-un oriciclu.

Pavarea apeirogonală de ordinul 2 reprezintă un diedru infinit în planul euclidian ca {∞,2}.

Cercul circumscris apeirogonului

Fiecare față apeirogonală este circumscrisă de un oriciclu, care arată ca un cerc în modelul discului Poincaré, tangent intern la frontiera cercului proiectiv (de la infinit).

Colorări uniforme

La fel ca la pavările planului euclidian, există 3 colorări uniforme ale pavării apeirogonale de ordinul 3, fiecare pentru domenii de reflexie diferite ale grupului triunghiului^⁠(d):

Regulată	Trunchiate
{∞,3}	t0,1{∞,∞}	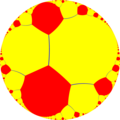t1,2{∞,∞}	t{∞[3]}
Grupului triunghiului hiperbolic
[∞,3]	[∞,∞]		[(∞,∞,∞)]

Simetrie

Duala: pavare triunghiulară de ordin infinit

Dualul acestei pavări reprezintă domeniile fundamentale ale simetriei [(∞,∞,∞)] (*∞∞∞). Există 15 subgrupuri de indici mici (7 unice) construite din [(∞,∞,∞)] prin îndepărtarea planelor de oglindire și alternare. Planele de oglindire pot fi eliminate dacă ordinul ramurilor sale este par și se reduce ordinul ramurilor învecinate la jumătate. Îndepărtarea a două plane de oglindire lasă un punct de rotație de ordin pe jumătate unde planele de oglindire îndepărtate se întâlnesc. În aceste imagini domeniile fundamentale sunt colorate alternativ alb-negru, iar planele de oglindire sunt situate la limitele dintre culori. Simetria poate fi dublată ca simetrie ∞∞2 prin adăugarea unui plan de oglindire care împarte în două domeniul fundamental. Împărțirea unui domeniu fundamental de către 3 plane de oglindire creează o simetrie ∞32.

Se construiește un subgrup mai mare [(∞,∞,∞^*)], de indice 8, deoarece (∞*∞^∞) cu punctele de rotație eliminate devine (*∞^∞).

Subgrupuri ale [(∞,∞,∞)] (*∞∞∞)
Indice⁠(d)	1	2			4
Diagramă
Coxeter	[(∞,∞,∞)]	[(1+,∞,∞,∞)] =	[(∞,1+,∞,∞)] =	[(∞,∞,1+,∞)] =	[(1+,∞,1+,∞,∞)]	[(∞+,∞+,∞)]
Orbifold	*∞∞∞	*∞∞∞∞			∞*∞∞∞	∞∞∞×
Diagramă
Coxeter		[(∞,∞+,∞)]	[(∞,∞,∞+)]	[(∞+,∞,∞)]	[(∞,1+,∞,1+,∞)]	[(1+,∞,∞,1+,∞)] =
Orbifold		∞*∞			∞*∞∞∞
Subgrupuri directe
Indice	2	4			8
Diagramă
Coxeter	[(∞,∞,∞)]+	[(∞,∞+,∞)]+ =	[(∞,∞,∞+)]+ =	[(∞+,∞,∞)]+ =	[(∞,1+,∞,1+,∞)]+ =
Orbifold	∞∞∞	∞∞∞∞			∞∞∞∞∞∞
Subgrupuri rădăcină
Indice	∞			∞
Diagramă
Coxeter	[(∞,∞*,∞)]	[(∞,∞,∞*)]	[(∞*,∞,∞)]	[(∞,∞*,∞)]+	[(∞,∞,∞*)]+	[(∞*,∞,∞)]+
Orbifold	∞*∞∞			∞∞

Poliedre și pavări înrudite

Această pavare este legată topologic ca parte a secvenței de poliedre regulate cu simbolul Schläfli {n,3}.

Variante de pavări regulate cu simetria *n62: {6,n}
Sferică	Euclidiană	Pavări hiperbolice
{6,2}	{6,3}	{6,4}	{6,5}	{6,6}	{6,7}	{6,8}	...	{6,∞}

Pavări uniforme paracompacte din familia [∞,3]
Simetrie: [∞,3], (*∞32)							[∞,3]+ (∞32)	[1+,∞,3] (*∞33)		[∞,3+] (3*∞)
		=	=	=				= or	= or	=
{∞,3}	t{∞,3}	r{∞,3}	t{3,∞}	{3,∞}	rr{∞,3}	tr{∞,3}	sr{∞,3}	h{∞,3}	h2{∞,3}	s{3,∞}
Duale uniforme
V∞3	V3.∞.∞	V(3.∞)2	V6.6.∞	V3∞	V4.3.4.∞	V4.6.∞	V3.3.3.3.∞	V(3.∞)3		V3.3.3.3.3.∞

Pavări uniforme paracompacte din familia [∞,∞]
= =	= =	= =	= =	= =	=	=
{∞,∞}	t{∞,∞}	r{∞,∞}	2t{∞,∞}=t{∞,∞}	2r{∞,∞}={∞,∞}	rr{∞,∞}	tr{∞,∞}
Pavări duale
V∞∞	V∞.∞.∞	V(∞.∞)2	V∞.∞.∞	V∞∞	V4.∞.4.∞	V4.4.∞
Alternări
[1+,∞,∞] (*∞∞2)	[∞+,∞] (∞*∞)	[∞,1+,∞] (*∞∞∞∞)	[∞,∞+] (∞*∞)	[∞,∞,1+] (*∞∞2)	[(∞,∞,2+)] (2*∞∞)	[∞,∞]+ (2∞∞)
h{∞,∞}	s{∞,∞}	hr{∞,∞}	s{∞,∞}	h2{∞,∞}	hrr{∞,∞}	sr{∞,∞}
Duale alternate
V(∞.∞)∞	V(3.∞)3	V(∞.4)4	V(3.∞)3	V∞∞	V(4.∞.4)2	V3.3.∞.3.∞

Pavări uniforme paracompacte din familia [∞,∞,∞]
(∞,∞,∞) h{∞,∞}	r(∞,∞,∞) h2{∞,∞}	(∞,∞,∞) h{∞,∞}	r(∞,∞,∞) h2{∞,∞}	(∞,∞,∞) h{∞,∞}	r(∞,∞,∞) r{∞,∞}	t(∞,∞,∞) t{∞,∞}
Pavări duale
V∞∞	V∞.∞.∞.∞	V∞∞	V∞.∞.∞.∞	V∞∞	V∞.∞.∞.∞	V∞.∞.∞
Alternări
[(1+,∞,∞,∞)] (*∞∞∞∞)	[∞+,∞,∞)] (∞*∞)	[∞,1+,∞,∞)] (*∞∞∞∞)	[∞,∞+,∞)] (∞*∞)	[(∞,∞,∞,1+)] (*∞∞∞∞)	[(∞,∞,∞+)] (∞*∞)	[∞,∞,∞)]+ (∞∞∞)
Duale alternate
V(∞.∞)∞	V(∞.4)4	V(∞.∞)∞	V(∞.4)4	V(∞.∞)∞	V(∞.4)4	V3.∞.3.∞.3.∞

Bibliografie

• en John H. Conway, Heidi Burgiel, Chaim Goodman-Strass, The Symmetries of Things 2008, ISBN: 978-1-56881-220-5 (Chapter 19, The Hyperbolic Archimedean Tessellations)
• en „Chapter 10: Regular honeycombs in hyperbolic space”. The Beauty of Geometry: Twelve Essays. Dover Publications. 1999. ISBN 0-486-40919-8. LCCN 99035678. 

Legături externe

• Materiale media legate de pavare apeirogonală de ordinul 3 la Wikimedia Commons
• en Eric W. Weisstein, Hyperbolic tiling la MathWorld.
• en Eric W. Weisstein, Poincaré hyperbolic disk la MathWorld.