Legile lui Kirchhoff

Legile lui Kirchhoff exprimă modul de conservare a energiei electrice într-un circuit electric. Au fost enunțate și dezvoltate de fizicianul german Gustav Robert Kirchhoff. Aceste teoreme se aplică în cazul rețelelor (circuitelor) electrice în curent continuu. O rețea electrică (circuit electric) e compusă din: ramuri de rețea (circuit), noduri de rețea (circuit) și ochiuri de rețea (circuit).

• Nod de rețea: reprezintă locul unde se întâlnesc cel puțin 3 conductoare ramuri (laturi) de rețea.
• O ramură de rețea reprezintă o distanță unilaterală conductoare dintre 2 noduri succesive.
• Ochi de rețea: este linia poligonală închisă formată din 3 sau mai multe laturi de rețea.

Prima lege a lui Kirchhoff

Suma intensităților curenților care intră într-un nod de rețea este egală cu suma intensităților curenților care ies din același nod. i₁ + i₄ = i₂ + i₃

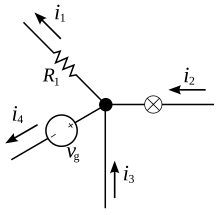
Prima lege a lui Kirchhoff (sau „legea nodurilor”) este o expresie a conservării sarcinii electrice într-un nod al unei rețele electrice. Conform acestei legi, suma intensităților curenților (continui) care intră într-un nod de rețea este egală cu suma intensităților curenților care ies din același nod.

Este evident că sarcina electrică totală ce intră într-un nod de rețea trebuie să fie egală cu sarcina electrică ce iese din acel nod:

$Q_{1}+Q_{4}=Q_{2}+Q_{3}$

Mișcarea sarcinilor electrice (ce intră și ies) efectuându-se în același timp (simultan), se poate scrie:

$i_{1}+i_{4}=i_{2}+i_{3}$,

adică: suma intensităților curenților care intră într-un nod de rețea este egală cu suma intensităților curenților (de curent continuu) care ies din același nod.

sau, altfel spus:

$i_{1}+i_{4}-i_{2}-i_{3}=0$

adică: suma algebrică a intensităților curenților electrici care se întâlnesc într-un nod de rețea este egală cu zero.

$\sum {i}_{k}=0$

Suma algebrică a tuturor căderilor de tensiune dintr-un ochi de rețea este egală cu zero. v₁ + v₂ + v₃ - v₄ = 0

A doua lege a lui Kirchhoff

A doua lege a lui Kirchhoff se referă la ochiuri de rețea și afirmă:

De-a lungul conturului unui ochi de rețea, suma algebrica a tensiunilor electromotoare ale surselor este egală cu suma algebrică a produselor dintre intensitatea curenților și rezistența totală de pe fiecare latură.

$\sum E_{n}=\sum R_{n}I_{n}$

sau

$v_{1}+v_{2}+v_{3}=v_{4}$

$v_{1}+v_{2}+v_{3}-v_{4}=0$

adică: suma algebrică a tensiunilor de-a lungul oricărui ochi de circuit este nulă.

$\sum V_{n}=0$

A doua lege a lui Kirchhoff poate fi reformulată astfel: Suma algebrică a tensiunilor (electromotoare și pe elemente rezistive) dintr-un un ochi de rețea este egală cu 0.

Importanță

Într-o rețea electrică se poate calcula căderea de potențial la bornele fiecărui rezistor și intensitatea curentului continuu în fiecare ramură (latură) de circuit aplicând cele două legi ale lui Kirchhoff: legea nodurilor și legea ochiurilor.

Pentru rezolvarea rețelelor electrice, folosind teoremele lui Kirchhoff, se parcurg următorii pași:

1. se identifică nodurile;
2. se identifică laturile, iar pe fiecare latură se alege un sens și se dă un nume intensității (de regulă, acestea vor fi necunoscutele);
3. se scrie prima lege de n-1 ori (n fiind numărul nodurilor);
4. se scriea a doua lege de atâtea ori încât numărul total de ecuații (obținute din cele două teoreme) să fie egal cu numărul necunoscutelor (intensitățile pe laturi);
5. se rezolvă numeric sistemul, obținându-se intensitățile pe laturi.

În mod practic, pentru un ochi de rețea se alege un sens de parcurgere. Dacă, în urma calculelor, unele intensități sunt negative, înseamnă că sensul real al curentului pe latura pe care s-a calculat intensitatea este invers decât s-a presupus inițial (valoarea numerică fiind corectă).

În accepțiunea celei de-a doua formulări a legii a doua a lui Kirchhoff, semnele tensiunilor se iau în considerare astfel:

• în cazul unei surse de tensiune, dacă sensul de parcurgere al ochiului coincide cu cel în care sursa tinde să producă un curent, atunci semnul acesteia este +; în caz contrar, semnul acesteia este -;
• în cazul elementelor rezistive, dacă sensul de parcurgere al ochiului coincide cu sensul curentului, tensiunea pe elementul respectiv se consideră negativă, iar în caz contrar este pozitivă.

Exemplu de calcul

Se dă circuitul din figură, unde se cunosc valorile rezistențelor r₁ = r₄ = 38 Ω, r₂ = r₃ = 8 Ω, r = 2 Ω, R = 10 Ω și valoarea curentului I = 10 A, cu sensul din figură. Se cere determinarea:

• valorii forței electromotoare E și a sensului ei;
• curenților care trec prin rezistențele r₁, r₂, r₃, r₄, și r.

Rezolvare

Folosind prima lege a lui Kirchhoff se obține:

• (nodul A):   $I=i_{1}+i_{2}$
• (nodul B):   $I=i_{3}+i_{4}$
• (nodul C):   $i_{1}=i+i_{3}$

Cu ajutorul celei de-a doua legi a lui Kirchhoff se obține:

• (circuitul ADBA):   $E-RI-r_{2}i_{2}-r_{4}i_{4}=0.$
• (circuitul ACDA):   $-r_{1}i_{1}-ri+r_{2}i_{2}=0.$
• (circuitul BCDB):   $-r_{3}i_{3}+ri+r_{4}i_{4}=0.$

Eliminând i₂ și i₄, se obține sistemul de 4 ecuații cu 4 necunoscute:

${\begin{cases}-i+i_{1}-i_{3}=0\\-E-8i_{1}-38i_{3}+560=0\\2i+46i_{1}=80\\2i-46i_{3}=-380\end{cases}}$

Rezolvând sistemul, se obține:

$E=240V,\;i=-6A,\;i_{1}=2A,\;i_{3}=8A,\;i_{2}=8A,\;i_{4}=2A.$

Bibliografie

• ,,Fizică: manual pentru clasa a X-a", Seryl Talpalaru, Dorel Haralamb, Constantin Corega
• ,,Fizică: formule și noțiuni generale - clasele VI-XII", Florin Măceșanu

Vezi și

• Analiză nodală
• Circuit electric

Legături externe

• Introducere in circuite electrice si electronice - Circuite divizoare si legile lui Kirchhoff pentru curent si tensiune