Curbă Bézier

În matematică, și anume în analiza numerică, o curbă Bézier este o curbă parametrică cu importante aplicații în grafica pe calculator și în domeniile asociate acesteia. Generalizările curbelor Bézier la dimensiuni superioare se numesc suprafețe Bézier, triunghiul Bézier fiind un caz particular al acestora.
Curbele Bézier au fost mediatizate în 1962 de inginerul francez Pierre Bézier, care le-a utilizat pentru a proiecta șasiuri de automobile. Curbele Bézier au fost dezvoltate în 1959 de Paul de Casteljau cu ajutorul algoritmului lui de Casteljau, o metodă numeric stabilă de evaluare a curbelor Bézier.
În grafica vectorială, curbele Bézier sunt o unealtă importantă folosită pentru modelarea curbelor derivabile și scalabile. Căile (în engleză Paths) așa cum sunt ele denumite adesea în programele de grafică vectorială sau de editare de imagini, cum ar fi Inkscape, Adobe Illustrator, Adobe Photoshop, sau GIMP sunt combinații de curbe Bézier interconectate. Căile nu au limitările imaginilor raster, iar modificarea lor este intuitivă. Curbele Bézier se folosesc și în animație pentru controlul mișcării în aplicații ca Adobe Flash, Adobe After Effects, Microsoft Expression Blend și Autodesk 3ds max.
Aplicații
[modificare | modificare sursă]Grafica pe calculator
[modificare | modificare sursă]Curbele Bézier sunt folosite în modelarea curbelor continue și derivabile în grafica pe calculator. Întrucât curba are proprietatea de înfășurătoare convexă (este conținută în poligonul convex definit de punctele sale de control), punctele pot fi afișate grafic și utilizate pentru manevrarea intuitivă a curbei. Transformările afine, cum ar fi translația, scalarea și rotația se pot aplica respectivei curbe prin aplicarea transformării similare asupra punctelor ei de control.
Cele mai des întâlnite curbe Bézier sunt cele cuadratice și cele cubice; evaluarea curbelor de grad superior este prea costisitoare în termeni de putere de calcul. Când sunt necesare forme mai complexe, se folosesc curbe Bézier concatenate, și nu curbe de grad superior. Unele programe de grafică, cum ar fi de exemplu Adobe Illustrator sau Inkscape, numesc aceste curbe concatenate căi. Aceste policurbe Bézier sunt reprezentate și în formatul de fișier SVG. Pentru a garanta derivabilitatea, punctul de control în care se întâlnesc cele două curbe și două puncte de control de fiecare parte a acestuia trebuie să fie coliniare.
Cea mai simplă metodă de redare (rasterizare) a unei curbe Bézier este evaluarea ei în multe puncte foarte apropiate și de a reda succesiunea corespunzătoare de segmente de dreaptă. Totuși, aceasta nu garantează că curba redată arată suficient de neted, deoarece punctele intermediare pot fi plasate prea departe unele de altele. În același timp, este posibil și să se genereze prea multe puncte acolo unde curba este aproape dreaptă. O metodă comună pentru adaptarea punctelor intermediare este subdivizarea recursivă, prin care se verifică punctele de control ale curbei pentru a afla dacă ea aproximează un segment de dreaptă cu o toleranță mică. Dacă nu aproximează un segment de dreaptă, curba este subîmpărțită parametric în două segmente, 0 ≤ t ≤ 0,5 și 0,5 ≤ t ≤ 1, și se aplică aceeași procedură recursiv pe fiecare jumătate.
Animație
[modificare | modificare sursă]În software-ul de animații, cum ar fi cazul Adobe Flash sau Adobe Shockwave, sau în aplicații ca Game Maker, curbele Bézier sunt folosite și pentru a trasa mișcarea. Utilizatorii subliniază calea dorită prin curbe Bézier, și aplicația creează cadrele necesare redării mișcării obiectului de-a lungul acelei căi.
Construcția și definiția unor curbe Bézier
[modificare | modificare sursă]Curbele liniare
[modificare | modificare sursă]
Curbele liniare sunt cazul cel mai simplu de curbă Bézier. Date fiind punctele P0 și P1, o curbă Bézier liniară este o linie dreaptă ce leagă cele două puncte. Expresia curbei este dată de
și este similară cu interpolarea liniară.
Parametrul t din expresia unei curbe Bézier liniare poate fi considerat a fi cât de departe este B(t) de P0 și P1. De exemplu, când t=0,25, B(t) a parcurs un sfert din distanța de la punctul P0 la P1. Pe măsură ce t variază de la 0 la 1, B(t) descrie o linie între P0 și P1.
Curbele Bézier cuadratice
[modificare | modificare sursă]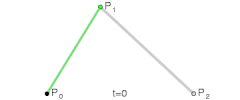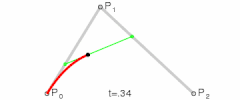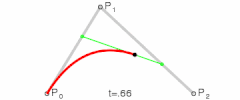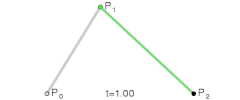
O curbă Bézier cuadratică este calea parcursă de funcția B(t), dacă sunt date punctele P0, P1, și P2,
O curbă Bézier cuadratică este un segment de parabolă.
Pentru curbele Bézier cuadratice, se pot construi puncte intermediare Q0 și Q1 astfel încât t variază de la 0 la 1:
- Punctul Q0 variază de la P0 la P1 și descrie o curbă Bézier liniară.
- Punctul Q1 variază de la P1 la P2 și descrie o curbă Bézier liniară.
- Punctul B(t) variază de la Q0 la Q1 și descrie o curbă Bézier cuadratică.
Fonturile TrueType folosesc spline-uri Bézier formate din curbe Bézier cuadratice.
Curbe Bézier cubice
[modificare | modificare sursă]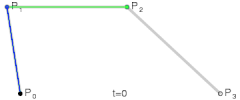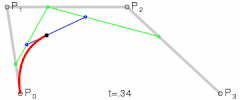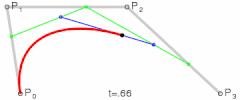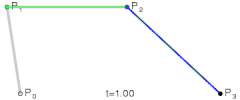
Patru puncte de control P0, P1, P2 și P3 din plan sau din spațiul tridimensional definesc o curbă Bézier cubică. Curba începe la P0, merge înspre P1 și ajunge la P3 din direcția lui P2. De regulă, ea nu trece nici prin P1 și nici prin P2; aceste puncte există doar pentru a furniza informația legată de direcție. Distanța dintre P0 și P1 determină „cât de mult timp” se mișcă curba în direcția lui P2 înainte de a se îndrepta spre P3.
Forma parametrică a curbei este:
Pentru curbele de grad superior, sunt necesare mai multe puncte de control. Pentru curbele cubice, se construiesc punctele Q0, Q1 și Q2 care descriu curbe Bézier liniare, și apoi punctele R0 și R1 care descriu curbe Bézier cuadratice.
Sistemele moderne de generale a imaginilor, cum sunt PostScript, Asymptote și Metafont folosesc spline-uri Bézier formate din curbe Bézier pentru desenarea formelor curbe.
Definiție generală
[modificare | modificare sursă]În general, o curbă Bézier de gradul se poate defini astfel: Date fiind punctele de control P0, P1,..., Pn, curba Bézier are expresia:
De exemplu, pentru :
Această formulă se poate exprima recursiv astfel: Fie curba Bézier determinată de punctele P0, P1,..., Pn. Atunci,
Cu alte cuvinte, curba Bézier de gradul este o interpolare liniară între două curbe Bézier de gradul .
Expresia unei curbe Bézier se poate scrie în funcție de polinoamele Bernstein de bază, astfel:
unde
sunt polinoamele Bernstein de gradul n, în care t0 = 1 și (1 - t)0 = 1.
Forma polinomială
[modificare | modificare sursă]Uneori, este de dorit să se exprime o curbă Bézier sub formă de polinom și nu de sumă de polinoame Bernstein. Aplicarea teoremei binomiale la definiția curbei, urmată de o rearanjare a termenilor, dă rezultatul:
unde
Această formulare este practică dacă poate fi calculat anterior evaluărilor lui .
Bibliografie
[modificare | modificare sursă]- Paul Bourke: Bézier Surfaces (in 3D), http://astronomy.swin.edu.au/~pbourke/curves/bezier/ Arhivat în , la Wayback Machine.
- Donald Knuth: Metafont: the Program, Addison-Wesley 1986, pp. 123–131.Discuție excelentă a detaliilor de implementare; distribuită gratuit împreună cu TeX.
- Dr Thomas Sederberg, BYU Bézier curves, http://www.tsplines.com/resources/class_notes/Bezier_curves.pdf Arhivat în , la Wayback Machine.
- J.D. Foley et al.: Computer Graphics: Principles and Practice in C (ediția a doua, Addison Wesley, 1992)

![{\displaystyle \mathbf {B} (t)=\mathbf {P} _{0}+t(\mathbf {P} _{1}-\mathbf {P} _{0})=(1-t)\mathbf {P} _{0}+t\mathbf {P} _{1}{\mbox{ , }}t\in [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/24758aca60716c16f5c8c48824a5f4bef6cbc19b)
![{\displaystyle \mathbf {B} (t)=(1-t)^{2}\mathbf {P} _{0}+2(1-t)t\mathbf {P} _{1}+t^{2}\mathbf {P} _{2}{\mbox{ , }}t\in [0,1].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ae58cba03138bd23af7a6f19458bd339011aee2b)
![{\displaystyle \mathbf {B} (t)=(1-t)^{3}\mathbf {P} _{0}+3(1-t)^{2}t\mathbf {P} _{1}+3(1-t)t^{2}\mathbf {P} _{2}+t^{3}\mathbf {P} _{3}{\mbox{ , }}t\in [0,1].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/037aa85c999e3e972d2e0d26926534c78e1aa3e7)

![{\displaystyle \mathbf {B} (t)=\sum _{i=0}^{n}{n \choose i}(1-t)^{n-i}t^{i}\mathbf {P} _{i}=(1-t)^{n}\mathbf {P} _{0}+{n \choose 1}(1-t)^{n-1}t\mathbf {P} _{1}+\cdots +t^{n}\mathbf {P} _{n}{\mbox{ , }}t\in [0,1].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f0e4f8a02c2b72cba1dfe1493785c08e831f691b)

![{\displaystyle \mathbf {B} (t)=(1-t)^{5}\mathbf {P} _{0}+5t(1-t)^{4}\mathbf {P} _{1}+10t^{2}(1-t)^{3}\mathbf {P} _{2}+10t^{3}(1-t)^{2}\mathbf {P} _{3}+5t^{4}(1-t)\mathbf {P} _{4}+t^{5}\mathbf {P} _{5}{\mbox{ , }}t\in [0,1].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ce0eb59d95c343d5e34e6505d4cd64ce1b968f33)



![{\displaystyle \mathbf {B} (t)=\sum _{i=0}^{n}\mathbf {b} _{i,n}(t)\mathbf {P} _{i},\quad t\in [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b386c714e76e16f8c55beffd6c3c0470cd070fd8)




