Șaua maimuței

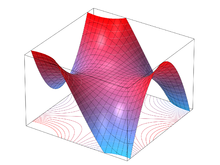
În matematică șaua maimuței este suprafața definită de ecuația

z=x^{3}-3xy^{2},

sau, în coordonate cilindrice,

z=\rho ^{3}\cos(3\varphi ).

Aparține clasei de suprafețe de tip șa, iar numele său derivă din observația că o șa pentru o maimuță ar necesita două îndoiri în jos (depresiuni) pentru picioare și una pentru coadă. Punctul $(0,0,0)$ de pe șaua maimuței corespunde unui punct critic degenerat^⁠(d) al funcției $z(x,y)$ la $(0,0)$ . Șaua maimuței are un punct ombilical^⁠(d) izolat cu curbură gaussiană^⁠(d) zero în origine, în timp ce curbura este strict negativă în toate celelalte puncte.

Ecuațiile se pot exprima și prin numere complexe $x+iy=re^{i\varphi }:$

z=x^{3}-3xy^{2}=\operatorname {Re} [(x+iy)^{3}]=\operatorname {Re} [r^{3}e^{3i\varphi }]=r^{3}\cos(3\varphi ).

Înlocuind 3 din ecuația în coordonate cilindrice cu orice număr întreg $k\geq 1,$ se poate crea o șa cu $k$ depresiuni.^[1]

O altă orientare a șeii maimuței este petala topită definită prin $x+y+z+xyz=0,$ astfel încât axa z a șeii maimuței să corespundă direcției $(1,1,1)$ a petalei topite.^[2]^[3]

Șaua ecvestră[modificare | modificare sursă]

Termenul de șa ecvestră poate fi folosit în contrast cu șaua maimuței, pentru a desemna o suprafață obișnuită în formă de șa, în care $z(x,y)$ are un punct șa, un minim sau maxim local în fiecare direcție a planului xy. În schimb, șaua maimuței are un punct de inflexiune staționar în fiecare direcție.

Note[modificare | modificare sursă]

^ en Peckham, S.D. (2011) Monkey, starfish and octopus saddles, Proceedings of Geomorphometry 2011, Redlands, CA, pp. 31-34, https://www.researchgate.net/publication/256808897_Monkey_Starfish_and_Octopus_Saddles
^ en J., Rimrott, F. P. (1989). Introductory Attitude Dynamics. New York, NY: Springer New York. p. 26. ISBN 9781461235026. OCLC 852789976.
^ en Chesser, H.; Rimrott, F.P.J. (1985). Rasmussen, H., ed. „Magnus Triangle and Smelt Petal”. CANCAM '85: Proceedings, Tenth Canadian Congress of Applied Mechanics, June 2-7, 1985, the University of Western Ontario, London, Ontario, Canada.

Legături externe[modificare | modificare sursă]

Portal Matematică

en Eric W. Weisstein, Monkey Saddle la MathWorld.

[1] Peckham, S.D. (2011) Monkey, starfish and octopus saddles, Proceedings of Geomorphometry 2011, Redlands, CA, pp. 31-34, https://www.researchgate.net/publication/256808897_Monkey_Starfish_and_Octopus_Saddles

[2] J., Rimrott, F. P. (1989). Introductory Attitude Dynamics. New York, NY: Springer New York. p. 26. ISBN 9781461235026. OCLC 852789976.

[3] Chesser, H.; Rimrott, F.P.J. (1985). Rasmussen, H., ed. „Magnus Triangle and Smelt Petal”. CANCAM '85: Proceedings, Tenth Canadian Congress of Applied Mechanics, June 2-7, 1985, the University of Western Ontario, London, Ontario, Canada.

[1]

[2]

[3]