Difracție

Schemă pentru fenomenul de difracție.

În fizică, difracția se referă la diverse fenomene asociate cu ocolirea de către unde a obstacolelor apărute în calea lor.

Difracția are loc în cazul oricărui tip de undă, inclusiv undele acustice, undele de la suprafața apei, și undele electromagnetice cum ar fi lumina vizibilă, razele x și undele radio. Întrucât obiectele materiale au și ele proprietăți ondulatorii, difracția apare și în cazul particulelor de substanță ca electroni, protoni, neutroni și poate fi studiată conform mecanicii cuantice.

În timp ce difracția are loc întotdeauna când undele întâlnesc obstacole în calea lor de propagare, efectele sale sunt în general cel mai pronunțate în cazul undelor a căror lungime de undă este de ordinul dimensiunii obstacolului. Șabloanele complexe rezultate din intensitatea unei unde difractate sunt rezultatul interferenței între diferite părți ale unei unde care au ajuns la observator urmărind căi diferite.

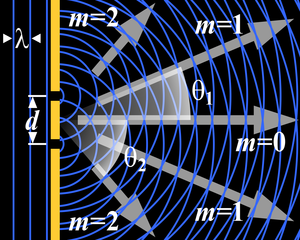
Pe ecranul $E_{2}$ se obține o imagine formată dintr-o succesiune de benzi (franje) luminoase alternate cu benzi întunecoase dispuse paralel cu fanta.

Notații consacrate utilizate

S - sursa de lumină monocromatică

$L_{1}$ - lentilă convergentă - transformă fasciculul convergent în fascicul paralel (undele sferice devin unde plane)

MN - fantă din paravanul $E_{1}$

$L_{2}$ - lentilă ce focalizează lumina difractată

Rețeaua de difracție

Rețeaua de difracție este formată din fante înguste, rectilinii, paralele, echidistante foarte apropiate.

n= numărul de trasături pe unitatea de lungime

N= numărul de zgârieturi rectilinii pe o distanță L

$n={\frac {N}{L}}.$ $\left(1\right)$

l= constanta rețelei

$l={\frac {L}{N}}={\frac {1}{n}}.$ $\left(2\right)$

Diferența de drum optic se scrie:

$\delta =l\left(\sin i-\sin \alpha \right).$ $\left(3\right)$

Determinarea maximelor, respectiv minimelor se face similar ca la interferență impunând condițiile:

$\delta =l\left(\sin i-\sin \alpha \right)=k\lambda .$ $\left(4\right)$

$\delta =l\left(\sin i-\sin \alpha \right)=k\lambda +{\frac {\lambda }{2}}.$ $\left(5\right)$

Determinarea lungimii de undă cu ajutorul rețelei optice

Deoarece $i=0$ relația (4) devine:

$\delta =l\left(\sin \alpha \right)=k\lambda .$ $\left(6\right)$

$n={\frac {1}{l}}.$ $\left(7\right)$

Pentru unghiuri mici:

$\tan \alpha ={\frac {x}{f}}=\sin \alpha ={\frac {k\lambda }{l}}.$ $\left(8\right)$

Deci:

$\lambda ={\frac {x}{kfn}}.$ $\left(9\right)$

Simulare pe calculator a șablonului de intensități produs de un laser de 663 nm incident pe o deschidere de 20x20 μm vizibilă pe un ecran aflat la 1 metru de deschidere

Difracție

Exemple de difracție în viața de zi cu zi

Efectele difracției pot fi ușor observate în viața de zi cu zi.

Cele mai des întâlnite exemple de difracție sunt cele de difracție a luminii; unul îl reprezintă banda spirală cu spațiere foarte mică, de pe un CD ori DVD care se comportă ca o rețea de difracție formând imaginea unui curcubeu în direcția discului. Acest principiu poate fi extins pentru a proiecta o rețea care să producă un șablon de difracție dorit; hologramele de pe cardurile de credit sau debit sunt și ele un exemplu.

Difracția atmosferică produsă de particulele fine pot cauza apariția unui halo (inel strălucitor în jurul unei surse de lumină puternice, ca soarele sau luna). Umbra unui obiect mat, produsă de lumina unei surse compacte, prezintă mici franje în jurul marginilor. Toate aceste efecte sunt consecințe ale faptului ca lumina este o undă.

Difracția poate apărea însă cu orice fel de undă. Undele de pe suprafața apei ocolesc obstacolele întâlnite în cale (bărci, pietre). Undele sonore ocolesc obiectele, motiv pentru care o persoană care vorbește de după un copac poate fi auzită. Difracția poate fi însă și o problemă în unele aplicații tehnice. Ea stabilește o limită fundamentală a rezoluției aparatelor foto, telescoapelor sau microscoapelor.

Vezi și

• Difracție Fresnel
• Difracție Fraunhofer
• Difracția electronilor
• Pata lui Poisson

Bibliografie

A. N. Tihonov, A. A. Samarski Ecuațiile fizicii matematice (traducere din limba rusă), Editura Tehnică, 1956