Utilizator:109.166.138.49

Traducere text

Moving a charge from a reference point to a specific point inside the field without producing an acceleration. Typically, the reference point is the Earth or a point at infinity, although any point can be used.

In classical electrostatics, the electrostatic field is a vector quantity which is expressed as the gradient of the electrostatic potential, which is a scalar quantity denoted by V or occasionally φ,[1] equal to the electric potential energy of any charged particle at any location (measured in joules) divided by the charge of that particle (measured in coulombs). By dividing out the charge on the particle a quotient is obtained that is a property of the electric field itself. In short, electric potential is the electric potential energy per unit charge.

This value can be calculated in either a static (time-invariant) or a dynamic (varying with time) electric field at a specific time in units of joules per coulomb (J C−1), or volts (V). The electric potential at infinity is assumed to be zero.

The electric potential at a point r in a static electric field E is given by the line integral

$V_{\mathbf {E} }=-\int _{C}\mathbf {E} \cdot \mathrm {d} {\boldsymbol {\ell }}\,$

where C is an arbitrary path connecting the point with zero potential to r. When the curl ∇ × E is zero, the line integral above does not depend on the specific path C chosen but only on its endpoints. In this case, the electric field is conservative and determined by the gradient of the potential:

$\mathbf {E} =-\mathbf {\nabla } V_{\mathbf {E} }.\,$

Then, by Gauss's law, the potential satisfies Poisson's equation:

$\mathbf {\nabla } \cdot \mathbf {E} =\mathbf {\nabla } \cdot \left(-\mathbf {\nabla } V_{\mathbf {E} }\right)=-\nabla ^{2}V_{\mathbf {E} }=\rho /\varepsilon _{0},\,$

where ρ is the total charge density (including bound charge) and ∇· denotes the divergence.

The concept of electric potential is closely linked with potential energy. A test charge q has an electric potential energy U_E given by

$U_{\mathbf {E} }=q\,V.\,$

The potential energy and hence also the electric potential is only defined up to an additive constant: one must arbitrarily choose a position where the potential energy and the electric potential are zero.

O sarcina electrică test are o energie potențială dată de:

$U_{\mathbf {E} }=q\,V.\,$

Energia potențială și astfel și potențialul electric este definit până la o constantă aditivă: este necesar de ales un punct arbitrar în care energia potentiala și potențialul electric sunt zero.

These equations cannot be used if the curl ∇ × E ≠ 0, i.e., in the case of a non-conservative electric field (caused by a changing magnetic field; see Maxwell's equations). The generalization of electric potential to this case is described below.

Le potentiel électrique, exprimé en volts (symbole : V), est l'une des grandeurs définissant l'état électrique d'un point de l'espace. Il correspond à l'énergie potentielle électrostatique que posséderait une charge électrique unitaire située en ce point, c'est-à-dire à l'énergie potentielle (mesurée en joules) d'une particule chargée en ce point divisée par la charge (mesurée en coulombs) de la particule.

La différence de potentiel électrique entre deux points de l'espace ou d'un circuit permet de calculer la variation d'énergie potentielle d'une charge électrique, ou de trouver plusieurs tensions inconnues dans un circuit électrique ou électronique.

Potentialul electric, exprimat in volti (V) e una din marimile definind starea electrica intr-un punct al spatiului. Corespunde energiei potentiale electrostatice pe care ar avea-o o sarcină electrică unitară situată în acest punct, adica energia potentiala a unei sarcini punct in acest punct raportata la sarcina particulei.

Diferența de potențial electric intre două puncte din spațiu permite calcularea variatiei energiei potentiale a unei sarcini electrice, sau de a afla mai multe tensiuni necunoscute intr-un circuit electric.

Para obter o potencial elétrico de um ponto, coloca-se nele uma carga de prova q e mede-se a energia potencial adquirida por ela. Essa energia potencial é proporcional ao valor de q. Portanto, o quociente entre a energia potencial e a carga é constante. Esse quociente chama-se potencial elétrico do ponto. Ele pode ser calculado pela expressão:

$V={\frac {E_{p}}{q}}\,$ , onde

• $V\,$ é o potencial elétrico,
• $E_{p}\,$ a energia potencial elétrica
• $q\,$ a carga.

Data una regione di spazio in cui è presente un campo elettrico conservativo, si definisce potenziale elettrico in un punto, il valore dato dal rapporto dell'energia potenziale elettrica rilevato da una carica elettrica di prova, posta in quel punto, e il valore della carica di prova. Il potenziale elettrico è dunque il rapporto tra l'energia potenziale elettrica, ossia il lavoro che deve compiere la forza dovuta al campo elettrico per spostare una o più cariche da quel punto fino all'infinito (ove si assume potenziale nullo), e la carica di prova.

Non potendo spostare una carica elettrica "fino all'infinito" si pone allora l'attenzione sulla energia "potenziale" liberabile da questa durante l'ipotetico movimento.

L'energia potenziale elettrica della carica è il livello di energia che la carica possiede a causa della sua posizione all'interno del campo elettrico, e pertanto il potenziale elettrico $V$ della carica di prova è definito operativamente come il rapporto tra l'energia potenziale $U$ e il valore della carica stessa, cioè:

$\operatorname {V} ={\frac {U_{E}}{q}}$

Il potenziale è dunque una quantità scalare e non dipende dal valore della carica di prova. La sua unità di misura è inoltre il volt: il punto A è al potenziale di 1 volt quando la forza elettrica compirebbe il lavoro di un Joule per portare una carica di un Coulomb libera di muoversi da A a all'infinito. Per estensione, si dice che tra due punti A e B esiste una differenza di potenziale di un volt se una forza elettrica compisse pari lavoro, sulla stessa carica, nello spostamento tra i due punti. Il lavoro $dW$ svolto dal campo elettrico $\mathbf {E} _{0}$ per un percorso infinitesimo $d\mathbf {s}$ su una carica $q$ è dato da:

$dW=q\mathbf {E} _{0}\cdot d\mathbf {s}$

e per calcolare il lavoro lungo una linea $l$ da un punto A ad un punto B:

$W=\int _{A}^{B}q\mathbf {E} _{0}\cdot d\mathbf {s}$

Si definiscono superfici equipotenziali per il potenziale elettrico le superfici in ogni punto delle quali il potenziale elettrico assume lo stesso valore. Questo implica che il lavoro del campo elettrico lungo una superficie equipotenziale è nullo ovunque perché è nulla la componente del campo elettrico parallela alla superficie, cioè il campo elettrico è ortogonale alla superficie equipotenziale.

Electric potential due to a point charge

Vezi și: Coulomb's law.

The electric potential created by a charge Q is V=Q/(4πε_or). Different values of Q will make different values of electric potential V (shown in the image).

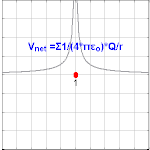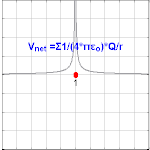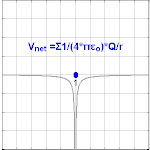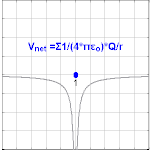
The electric potential arising from a point charge Q, at a distance r from the charge is observed to be

$V_{\mathbf {E} }={\frac {1}{4\pi \varepsilon _{0}}}{\frac {Q}{r}},\,$

where ε₀ is the permittivity of vacuum.Format:Physconst $V_{\mathbf {E} }$ is known as the Coulomb potential.

The electric potential for a system of point charges is equal to the sum of the point charges' individual potentials. This fact simplifies calculations significantly, because addition of potential (scalar) fields is much easier than addition of the electric (vector) fields.

(The equation given above for the electric potential (and all the equations used here) are in the forms required by SI units. In some other (less common) systems of units, such as CGS-Gaussian, many of these equations would be altered.)

Dal momento che per il teorema di Helmholtz si può sempre definire una funzione scalare $V_{0}$ il cui gradiente, cambiato di segno, coincida con il campo $\mathbf {E} _{0}$:

$\mathbf {E} _{0}=-\nabla V_{0}$

il potenziale elettrico nel vuoto per una carica puntiforme è dato da:

$V_{0}(r)={\frac {1}{4\pi \varepsilon _{0}}}{\frac {Q}{r}}+cost$

Il potenziale elettrico è quindi definito a meno di una costante arbitraria, essendo il gradiente di una costante nullo. Questo non rappresenta un problema pratico, poiché normalmente interessa conoscere la differenza di potenziale $-\Delta V_{0}$, più che il valore del potenziale elettrico in un punto. Convenzionalmente, la costante viene determinata considerando nullo il potenziale che una carica puntiforme produce all'infinito.

In coordinate cartesiane, si ha:

$\mathbf {E} _{0}\,=\,\left(-{\frac {\partial V_{0}}{\partial x}},-{\frac {\partial V_{0}}{\partial y}},-{\frac {\partial V_{0}}{\partial z}}\right)$

Distribuzione di cariche puntiformi

Una volta introdotta la definizione di potenziale per una carica puntiforme, per il principio di sovrapposizione lineare è possibile generalizzare la definizione del potenziale nel vuoto generato da una distribuzione di cariche puntiformi $q_{1},q_{2},...,q_{n}$, disposte nello spazio nelle posizioni $r_{1},r_{2},...,r_{n}$:

$\mathbf {E} _{0i}=-\nabla V_{0i}$

ovvero:

$\mathbf {E} _{0}(P)=\sum _{i=1}^{n}{\frac {q_{i}}{4\pi \varepsilon _{0}}}{\frac {(\mathbf {r} _{i}-\mathbf {r} )}{\left|\mathbf {r} _{i}-\mathbf {r} \right|^{3}}}$

Distribuzione continua di cariche

Poiché la carica elettrica è quantizzata, (non è stata sinora dimostrata l'esistenza in Natura di cariche elettriche libere inferiori a quelle di un elettrone) a rigore non esistono distribuzioni continue di carica elettrica. Tuttavia, in un corpo esteso le cariche elementari sono in numero talmente elevato che è conveniente utilizzare il formalismo infinitesimale ed introdurre la densità di carica volumetrica $\rho =dq/dv$, superficiale $\sigma =dq/dS$ e lineare $\lambda =dq/dl$. In questo modo il potenziale elettrico in un punto dello spazio $(x,y,z)$ generato da una sorgente estesa con carica totale

$Q=\int _{v}\rho (x',y',z'){dx}'{dy}'{dz}'\$

è dato dall'integrale:

$V_{0}(P)={\frac {1}{4\pi \varepsilon _{0}}}\int _{v}{\frac {\rho (x',y',z')}{r-r'}}{dx}'{dy}'{dz}'\$

in cui $r$ è la distanza dall'origine del punto P e $r'$ è la distanza dall'origine del volume infinitesimale $dv'={dx}'{dy}'{dz}'$.

Potencial e campo nos condutores

Consideremos um condutor cilíndrico e retilíneo com os dois extremos ligados aos terminais de uma bateria. Entre os extremos do condutor existirá uma diferença de potencial. Se A for o extremo que está ligado ao terminal negativo e B o extremo ligado ao terminal positivo, o potencial será maior em B do que em A: VB > VA.

As cargas de condução no condutor deslocam-se na direção do campo elétrico; no mesmo sentido do campo, se forem cargas positivas, ou no sentido oposto se forem negativas. Assim, as linhas de campo elétrico deverão ser retas paralelas ao eixo do cilindro. Portanto, o campo tem módulo E constante e segue a direção do deslocamento d s ao longo do condutor; o integral de linha que define a diferença de potencial , pode ser calculado facilmente:

$\int \limits _{B}^{A}E\;ds=V_{B}-V_{A}\quad \Rightarrow \quad V_{B}-V_{A}=E\;\Delta s$

onde $\Delta s$ é o comprimento do condutor. Assim, o módulo do campo no condutor é igual à diferença de potencial entre os seus extremos, dividida pelo seu comprimento:

$E={\frac {\Delta V}{\Delta s}}$

O resultado anterior também mostra que o campo aponta sempre desde o ponto com maior potencial até o ponto com menor potencial, já que para obtermos um resultado positivo, tivemos que integrar desde B até A.

Corrente e campo elétrico em dois condutores diferentes, ligados à mesma diferença de potencial

Se o condutor na figura acima for um semicondutor tipo N, as cargas de condução negativas deslocam-se no sentido oposto ao campo e, portanto, a corrente é no sentido do campo. Se o semicondutor for do tipo P, as cargas de condução positivas deslocam-se no sentido do campo e a corrente também é no sentido do campo. Consequentemente, independentemente o tipo de condutor ou semicondutor, a corrente será sempre na direção e sentido do campo elétrico, nomeadamente, desde o extremo com maior potencial para o extremo com menor potencial.

Se o condutor não for retilíneo, como no lado direito da figura, as linhas de campo já não são retas mas seguirão a direção do condutor. Isso implica que o campo vetorial ${\vec {E}}$ não é constante, mas se o condutor for homogéneo, as separação entre as linhas será sempre igual, indicando que o módulo E do campo é constante.

Dezplazamiento

Considérese una carga eléctrica puntual $q$ en presencia de un campo eléctrico ${\vec {E}}$. La carga experimentará una fuerza eléctrica:

${\vec {F}}=q{\vec {E}}\,\!$ |1|

Esta fuerza realizará un trabajo para trasladar la carga o elemento de un punto A a otro B, de tal forma que para producir un pequeño desplazamiento $dl$ la fuerza eléctrica hará un trabajo diferencial $dW$ expresado como:

$dW={\vec {F}}\cdot d{\vec {l}}=q{\vec {E}}\cdot d{\vec {l}}\,\!$ |2|

Por lo tanto, integrando la expresión {{|2}} se obtiene el trabajo total realizado por el campo eléctrico:

$W=\int _{A}^{B}q{\vec {E}}\cdot d{\vec {l}}\,\!$ |3|

Un caso particular de la fórmula anterior, es el del caso de un campo eléctrico creado por una carga puntual estática Q. Sea una carga puntual $q$ que recorre una determinada trayectoria A - B en las inmediaciones de una carga $Q$ tal y como muestra la figura 1. Siendo $dr$ el desplazamiento infinitesimal de la carga $q$ en la dirección radial, el trabajo diferencial $dW$ se puede expresar así:

{{|$W=\int {\vec {F}}\cdot d{\vec {l}}=\int F\,dl\cos(\theta )=\int F\,dr\,\!$|4|center}}

Para calcular el trabajo total, se integra entre la posición inicial A, distante $r_{A}\,\!$ de la carga $Q$ y la posición final B, distante $r_{B}\,\!$ de la carga $Q$:

| $W=\int _{r_{A}}^{r_{B}}Fdr=\int _{r_{A}}^{r_{B}}{\frac {1}{4\pi {\epsilon }_{0}}}{\frac {Qq}{r^{2}}}\,dr={\frac {Qq}{4\pi {\epsilon }_{0}}}\left({\frac {1}{r_{A}}}-{\frac {1}{r_{B}}}\right)$ |5|center}}

En la expresión Format:Eqnref, $\epsilon _{0}$ es la permitividad del vacío; de dicha expresión se concluye que el trabajo $W$ no depende de la trayectoria seguida por la partícula, sólo depende de la posición inicial y final, lo cual implica que la fuerza eléctrica ${\vec {F}}\,\!$ es una fuerza conservativa. Por lo tanto se puede definir una energía potencial que permite calcular el trabajo más fácilmente:

$E_{p}={\frac {1}{4\pi {\epsilon }_{0}}}{\frac {Qq}{r}}$|6|center

El trabajo realizado por la fuerza eléctrica para desplazar una partícula entre A y B será:

$W=-\Delta E_{p}=E_{p_{A}}-E_{p_{B}}$|7|center}}

Usualmente, el nivel cero de energía potencial se suele establecer en el infinito, es decir, si y sólo si $r=\infty \rightarrow E_{p}=0\,\!$ (esto tiene que ver con la elección de la constante de integración en la fórmula del potencial).

Versiune ro

Potențialul electric e energia potențială electrică per unitate de sarcină electrică.--109.166.138.49 (discuție) 17 decembrie 2019 14:19 (EET)

Câmpul electric este exprimat ca gradient cu semn schimbat al unei mărimi scalare denumite potențial.

Sarcina punct

Potențialul electric datorat unei sarcini punct Q la distanța r e:

$V_{\mathbf {E} }={\frac {1}{4\pi \varepsilon _{0}}}{\frac {Q}{r}}+Const\,$

Constanta poate fi nula. In mod uzual interesează diferența de potențial electric $-\Delta V_{0}$, astfel constanta dispare. Constanta e zero prin alegerea punctului de la infinit cu valoare zero a potențialului.

Sistem de sarcini punctuale

Potențialul electric al unui sistem de sarcini punctuale e suma potențialelor individuale ale sarcinilor punctuale. Această proprietate permite simplificarea calculelor.