Omotetie

Un pantograf.

În geometrie, omotetia exprimă într-o formă algebrică asemănarea a două figuri.

Exemple

Pentru a ilustra o omotetie nu este nevoie de 2, 3 sau mai multe dimensiuni

Cel mai simplu exemplu este dat de către o riglă.

Vârful 0 este centrul de omotetie.

Punctul 1 este transportat, de pildă, în punctul 4, printr-o omotetie de centru 0 și raport patru ; putem scrie foarte bine :

04 = 01 + 12 + 23 + 34 = 01 + 01 + 01 + 01 = patru × 01

sau, pe scurt,

04 = patru × 01,

și încă :

4 = 0 + patru × 01

Un mod răspândit de a nota informația de mai sus este :

$1\mapsto 0+\lambda {\overrightarrow {01}},$

unde λ = patru. Dificultatea la citire este dată de faptul că semnul + este folosit ca o adunare între două tipuri distincte de obiecte : în stânga puncte iar în dreapta, segmente orientate. Astfel de abuzuri de notație sunt acceptate în matematică, pentru a nu încărca o formulă cu prea feluri de multe semne.

Teorema lui Thales

Segmentul DE este transformat în segmentul BC printr-o omotetie de centru A și raport 3:2

Folosind notația de mai sus, o configurație de cinci puncte legate prin teorema lui Thales poate fi descrisă astfel :

$D\mapsto B=A+\lambda {\overrightarrow {AD}},$

$E\mapsto C=A+\lambda {\overrightarrow {AE}}$

unde coeficientul (sau raportul de omotetie) λ este aproximativ 3/2 (pentru desenul din imagine).

Teorema lui Desargues

O configurație de șapte puncte legate prin teorema lui Desargues

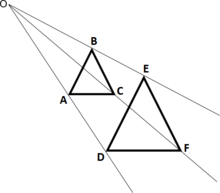
Folosind notația de mai sus, o configurație de șapte puncte legate prin teorema lui Desargues poate fi descrisă astfel:

$A\mapsto D=O+\lambda {\overrightarrow {OA}},$

$B\mapsto E=O+\lambda {\overrightarrow {OB}},$

$C\mapsto F=O+\lambda {\overrightarrow {OC}}$

Echivalent, se poate scrie la fel de bine:

$OD=\lambda {\overrightarrow {OA}},$

$OE=\lambda {\overrightarrow {OB}},$

$OF=\lambda {\overrightarrow {OC}}$

Avantaje

Noțiunea de omotetie aduce în plus, în geometrie, coeficientul $\lambda$.

În geometria riglei și a compasului, numerele care pot lua locul lui $\lambda$ nu ajung pentru a putea trisecta un unghi, dubla un cub sau pentru a face cuadratura cercului.

Însă dacă asemanarea a două obiecte a fost descrisă folosind relațiile de omotetie, geometria riglei și a compasului poate fi riguros generalizată la alte geometrii care corespund corpului de ”coeficienți”, oricât de sărac sau de bogat în numere ar fi acesta.

Astfel, $\lambda$ poate fi un număr algebric, un număr real, un număr complex sau alt număr dintr-un corp oarecare. În plus, noțiunea de asemănare transcrisă astfel poate fi (și este) implementată în programele de calculator.

Bibilografie

• Dicționar Tehnic Poliglot, română, rusă, engleză, germană, franceză, spaniolă, ediția a doua, Editura Tehnică, București 1967
• Michèle Audin, Géométrie, EDP Sciences, 2006