Izogonal conjugat

Drepte izogonal conjugate.

Izogonal conjugatul lui P.

Transformarea izogonal conjugată efectuată asupra punctelor din interiorul triunghiului.

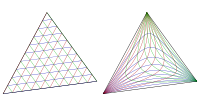
Oricare două drepte AX și AY se numesc izogonal conjugate în raport cu triunghiul ABC dacă $\angle XAY$ are aceeași bisectoare ca a $\angle BAC$.

Punctul izogonal conjugat al unui punct P în raport cu triunghiul ABC se construiește prin reflexia dreptelor PA, PB și PC față de bisectoarele unghiurilor A, B și C.

Punctul izogonal conjugat al lui P este punctul P* din figură. Punctul izogonal conjugat al lui P* is P.

Punctul izogonal conjugat al centrului cercului înscris este el însuși I.

Punctul izogonal al ortocentrului H este centrul O al cercului circumscris triunghiului.

Punctul izogonal conjugat al centrului de greutate G al triunghiului este (prin definiție) punctul simedian K.

În coordonate triliniare, dacă X = x : y : z este un punct care nu se află pe laturile triunghiului ABC, atunci izogonalul lui conjugat este 1/x : 1/y : 1/z. Din acest motiv, izogonalul conjugat al lui X se mai notează prin X ⁻¹.

Setul S de centre ale triunghiurilor dat de produsul trilinear definit prin:

(p : q : r) * (u : v : w) = pu : qv : rw,

este un grup comutative, iar inversul fiecărui punct X din S este X ⁻¹.

Vezi și

• Izotomic conjugate
• Punctul lui Brocard

Legături externe

• Interactive Java Applet illustrating isogonal conjugate and its properties Arhivat în 19 martie 2011, la Wayback Machine.
• MathWorld
• Pedal Triangle and Isogonal Conjugacy