Demonstrație fără divulgare de cunoștințe

În criptografie, o demonstrație fără divulgare de cunoștințe sau un protocol fără divulgare de cunoștințe este o metodă prin care o parte (demonstratorul) poate dovedi altei părți (verificatorul) că o anumită afirmație este adevărată, evitând în același timp să transmită verificatorului orice informație în plus față de de simplu fapt al adevărului afirmației.^[1] Intuiția care stă la baza demonstrațiilor fără divulgare de cunoștințe este aceea că este trivial să dovedești deținerea anumitor informații prin simpla dezvăluire a lor; provocarea este de a dovedi această posesie fără a dezvălui informațiile sau orice aspect ale acestora.^[2]

Având în vedere faptul că ar trebui să se poată genera o demonstrație a unei afirmații numai atunci când deține anumite informații secrete legate de acea afirmație, verificatorul, chiar și după ce s-a convins de adevărul afirmației, ar trebui totuși să rămână în imposibilitatea de a dovedi afirmația către terți.

În modelul simplu, demonstrațiile netriviale fără divulgare de cunoștințe (adică cele pentru limbaje din afara clasei de complexitate BPP ) necesită interacțiune între demonstrator și verificator.^[3] Această interacțiune implică de obicei selectarea de către verificator a uneia sau mai multor provocări aleatorii; faptul că aceste provocări sunt aleatorii, împreună cu răspunsurile corecte ale demonstratorului la acestea, în ciuda naturii lor aleatoare, au scopul de a convinge verificatorul că demonstratorul deține cunoștințele pretinse. Dacă interacțiunea nu ar fi prezentă, atunci verificatorul, după ce a obținut transcrierea de execuție a protocolului, adică singurul mesaj al demonstratorului, ar putea reda acea transcriere unei terțe părți, convingând astfel această terță parte (în mod eronat) că și verificatorul deținea informațiile secrete.

Vorbitorii de limbă engleză folosesc abrevierea ZKIP pentru Zero Knowledge Interactive proof.

În modelele obișnuite ale șirurilor aleatoare și ale oracolului aleatoriu, există și demonstrații non-interactive fără divulgare de cunoștințe, drept consecință a euristicii Fiat-Shamir.^[4]^[5]^[6] În practică, aceste demonstrații se bazează pe ipoteze de calcul (de obicei, rezistența la coliziune a unei funcții hash criptografice ).

Exemple abstracte

Peștera lui Ali Baba

Există o poveste binecunoscută care prezintă ideile fundamentale ale demonstrațiilor fără divulgare de cunoștințe, publicată pentru prima dată în 1990 de Jean-Jacques Quisquater și alții în lucrarea lor „Cum să explici copiilor tăi protocoalele fără divulgare de cunoștințe”.^[7] Cele două părți din povestea cu demonstrații fără divulgare de cunoștințe sunt Denisa ca demonstrator și Victor, verificatorul demonstrației.

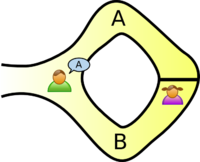
În această poveste, Denisa a descoperit cuvântul secret folosit pentru a deschide o ușă magică într-o peșteră. Peștera are forma unui inel, cu intrarea pe o parte și ușa magică blocând partea opusă. Victor vrea să știe dacă Denisa cunoaște cuvântul secret; dar Denisa, fiind o persoană foarte privată, nu vrea să-și dezvăluie cunoștințele (cuvântul secret) lui Victor și nici să dezvăluie lumii ceea ce cunoaște.

Ei etichetează cu A și B căile din stânga și din dreapta de la intrare. Mai întâi, Victor așteaptă în afara peșterii când Denisa intră. Denisa o ia fie pe calea A, fie pe calea B; Victor nu are voie să vadă pe ce drum o ia. Apoi, Victor intră în peșteră și strigă numele căii pe care vrea ca Denisa să o folosească pentru a se întoarce, fie A sau B, aleasă la întâmplare. Dacă Denisa cunoaște într-adevăr cuvântul magic, acest lucru este îi este ușor: deschide ușa, dacă este necesar, și se întoarce pe calea dorită.

Totuși, să presupunem că ea nu știa cuvântul. În acest caz, ea s-ar putea întoarce pe calea numită doar dacă Victor ar striga numele aceleiași căi pe care a intrat ea. Deoarece Victor alege A sau B la întâmplare, ea ar avea șanse de 50% să ghicească corect. Dacă cei doi ar repeta acest joc de multe ori, să zicem de 20 de ori la rând, șansa ei de a anticipa cu succes toate cererile lui Victor ar fi redusă la 1 în 2 ²⁰, sau 9,56 × 10 ⁻⁷.

Astfel, dacă Denisa apare în mod repetat la ieșirea pe care o numește Victor, el poate concluziona că este extrem de probabil ca Denisa să cunoască, de fapt, cuvântul secret.

O observație cu privire la observatorii terți: chiar dacă Victor poartă o cameră ascunsă care înregistrează întreaga tranzacție, singurul lucru pe care camera îl va înregistra este într-un caz Victor strigând „A!” iar Denisa apărând la A sau în celălalt caz Victor strigând "B!" și Denisa apărând la B. O înregistrare de acest tip ar fi trivială pentru oricare doi oameni să o falsifice (cerând doar ca Denisa și Victor să se pună de acord în prealabil asupra secvenței de A și B pe care Victor o va striga). Cu siguranță, o astfel de înregistrare nu va fi niciodată convingătoare pentru nimeni, în afară de participanții inițiali. De fapt, chiar și o persoană care a fost prezentă ca observator la experimentul inițial nu ar fi convins, deoarece Victor și Denisa ar fi putut orchestra întregul „experiment” de la început până la sfârșit.

Dacă însă Victor alege A și B dând cu banul în timp ce se filmează, acest protocol își pierde proprietatea de a nu divulga cunoștințe; filmarea aruncării monedei ar fi probabil convingătoare pentru orice persoană care urmărește înregistrarea mai târziu. Astfel, deși acest lucru nu îi dezvăluie cuvântul secret lui Victor, îi permite lui Victor să convingă pe oricune că Denisa are aceste cunoștințe – contrar dorințelor declarate ale Denisei. Cu toate acestea, criptografia digitală e în general bazată pe „dat cu banul”, bazându-se pe un generator de numere pseudoaleatoare, care este asemănător unei monede cu un model fix de distribuție de cap și pajură, cunoscut doar de proprietarul monedei. Dacă moneda lui Victor s-ar comporta în acest fel, atunci din nou ar fi posibil ca Victor și Denisa să fi falsificat experimentul, așa că utilizarea unui generator de numere pseudoaleatoare nu ar dezvălui lumii cunoștințele Denisei în același mod în care ar fi făcut-o folosind folosirea unei monede.

Observați că Denisa i-ar putea demonstra lui Victor că știe cuvântul magic, fără să i-l dezvăluie, dintr-o singură încercare. Dacă atât Victor, cât și Denisa merg împreună la gura peșterii, Victor o poate vedea pe Denisa intrând prin A și ieșind prin B. Acest lucru ar dovedi cu certitudine că Denisa cunoaște cuvântul magic, fără să-i dezvăluie cuvântul magic lui Victor. Cu toate acestea, o astfel de dovadă ar putea fi observată de un terț sau înregistrată de Victor și o astfel de dovadă ar fi convingătoare pentru oricine. Cu alte cuvinte, Denisa nu ar putea respinge o astfel de dovadă susținând că s-a înțeles cu Victor; prin urmare, nu ar mai deține controlul asupra celor pe care îi alege să își dezvăluie cunoștințele.

Două bile și prietenul daltonist

Imaginează-ți că prietenul tău „Victor” este daltonist roșu-verde (în timp ce tu nu ești) și ai două bile: una roșie și una verde, dar în rest identice. Pentru Victor, bilele par complet identice. Victor este sceptic că bilele pot fi de fapt diferențiate. Vrei să-i demonstrezi lui Victor că bilele sunt de fapt colorate diferit, dar nimic altceva. Mai ales, nu vrei să dezvălui care bilă este cea roșie și care este cea verde.

Iată sistemul de demonstrație. Îi dai cele două bile lui Victor și le ascunde la spate. Apoi, scoate una dintre bile și o arată. Apoi o ascunde din nou la spate și apoi scoate și arată iar una dintre cele două bile, la întâmplare, cu aceeași probabilitate. Te va întreba: „Am schimbat bila?” Toată această procedură se repetă ori de câte ori este necesar.

Privind culorile bilelor, poți, desigur, să spui cu certitudine dacă le-a schimbat sau nu. Pe de altă parte, dacă bilele ar fi de aceeași culoare și, prin urmare, imposibil de distins, nu ai putea ghici corect cu o probabilitate mai mare de 50%.

Deoarece probabilitatea ca ai fi reușit aleatoriu să identifici fiecare schimbare/ne-schimbare este de 50%, probabilitatea de a fi reușit aleatoriu la toate schimbările/ne-schimbările se apropie de zero („corectitudine”). Dacă tu și prietenul tău repetați această „demonstrație” de mai multe ori (de exemplu, de 20 de ori), prietenul tău ar trebui să se convingă („completitudine”) că bilele sunt într-adevăr de culoare diferită.

Demonstrația de mai sus este fără divulgare de cunoștințe pentru că prietenul tău nu învață niciodată care minge este verde și care este roșie; într-adevăr, el nu obține cunoștințe despre cum să distingă bilele.^[8]

Unde e Waldo

Un exemplu binecunoscut de demonstrație fără divulgare de cunoștințe este exemplul „Unde este Waldo”. În acest exemplu, demonstratorul dorește să-i demonstreze verificatorului că știe unde se află Waldo pe o pagină din cartea Unde este Waldo?, fără a dezvălui verificatorului locația sa.^[9]

Demonstratorul începe prin a lua o placă mare neagră cu o mică gaură în ea, de dimensiunea lui Waldo. Placa are de două ori dimensiunea cărții în ambele direcții, astfel încât verificatorul nu poate vedea unde pe pagină o plasează demonstratorul. Demonstratorul pune apoi placa peste pagină, astfel încât Waldo să fie vizibil prin gaură.^[9]

Verificatorul poate privi acum prin gaură și îl poate vedea pe Waldo, dar nu poate vedea nicio altă parte a paginii. Prin urmare, demonstratorul a dovedit verificatorului că știe unde se află Waldo, fără a dezvălui alte informații despre locația sa.^[9]

Acest exemplu nu este o demonstrație fără divulgare de cunoștințe perfectă, deoarece demonstratorul dezvăluie unele informații despre locația lui Waldo, cum ar fi poziția corpului său. Cu toate acestea, este o ilustrare decentă a conceptului de bază al unei demonstrații fără divulgare de cunoștințe.

Sudoku

În acest exemplu, Denisa vrea să îi demonstreze lui Victor că știe soluția unei grile de Sudoku^[10].

Pentru a face acest lucru, după ce a rezolvat grila de Sudoku, Denisa decupează cu grijă grila cu foarfecele. În urma acestui proces, ea obține 81 de pătrate mici de hârtie pe care sunt scrise numerele grilei de Sudoku rezolvate. Ea întoarce apoi bucățile de hârtie cu fața în jos, cu excepția numerelor care erau scrise la început pe grilă (cele prezente înainte de a fi început să rezolve grila). Procedura de demonstrare poate începe.

Victor poate alege orice rând, coloană sau pătrat de 3x3. Denisa ia cele 9 pătrate de hârtie corespunzătoare, le amestecă cu grijă și i le dă lui Victor. Victor poate verifica apoi dacă aceste pătrate conțin numerele de la 1 la 9. Apoi, Denisa pune din nou pătratele mici la locul lor cu fața în jos pe grilă. Victor repetă procedura până când a verificat cele 9 rânduri, 9 coloane și 9 pătrate 3x3 ale grilei Sudoku.

La sfârșitul acestui proces, Victor are dovada că Denisa a rezolvat grila Sudoku, fără însă să fi aflat nimic suplimentar despre grilă.

Definiție

O demonstrație fără divulgare de cunoștințe a unei afirmații trebuie să satisfacă trei proprietăți:

Completitudine (completeness): dacă afirmația este adevărată, un verificator onest (adică unul care urmează protocolul în mod corespunzător) va fi convins de acest fapt de un demonstrator onest.
Corectitudine (soundness): dacă afirmația este falsă, niciun demonstrator trișor nu poate convinge un verificator onest că afirmația este adevărată, decât cu probabilitate redusă.
Nici o informație suplimentară (zero-knowledge): dacă afirmația este adevărată, niciun verificator nu învață altceva decât faptul că afirmația este adevărată. Cu alte cuvinte, doar cunoașterea afirmației (nu a secretului) este suficientă pentru a imagina un scenariu care arată că cel care dovedește cunoaște secretul. Acest lucru este formalizat arătând că fiecare verificator are un simulator care, pornind doar de la afirmația care trebuie demonstrată (și fără acces la demonstrator), poate produce o transcriere care „pare” o interacțiune între un demonstrator onest și verificatorul în cauză.

Primele două dintre aceste proprietăți caracterizează noțiunea mai generală a sistemelor de demonstrare interactive. Al treilea este ceea ce face ca demonstrația să fie fără divulgare de cunoștințe.^[11]

Demonstrațiile fără divulgare de cunoștințe nu sunt demonstrații în sensul matematic al termenului, deoarece există o mică probabilitate, eroarea de corectitudine, ca un demonstrator trișor să poată convinge verificatorul de o afirmație falsă. Cu alte cuvinte, demonstrațiile fără divulgare de cunoștințe sunt „demonstrații” probabiliste mai degrabă decât demonstrații deterministe. Cu toate acestea, există tehnici pentru a reduce eroarea de corectitudine la valori neglijabil de mici (de exemplu, ghicirea corectă a unei sute sau mii de decizii binare are o eroare de corectitudine de $1/2^{100}$ sau $1/2^{1000}$ , respectiv. Pe măsură ce numărul de biți crește, eroarea de corectitudine scade spre zero).

O definiție formală a proprietății de nedivulgare a cunoștințelor trebuie să folosească un model de calcul, cel mai comun fiind cel al unei mașini Turing. Fie $D$ , $V$ și $S$ mașini Turing. Un sistem de demonstrare interactiv cu $(D,V)$ pentru un limbaj $L$ este fără divulgare de cunoștințe dacă pentru orice verificator probabilistic de timp polinomial (PPT). ${\hat {V}}$ există un simulator PPT $S$ astfel încât:

\forall x\in L,z\in \{0,1\}^{*},\operatorname {Transcriere} _{\hat {V}}\left[D(x)\leftrightarrow {\hat {V}}(x,z)\right]=S(x,z)

Unde $\operatorname {Transcriere} _{\hat {V}}\left[D(x)\leftrightarrow {\hat {V}}(x,z)\right]$ este o înregistrare a interacțiunilor dintre $D(x)$ și ${\hat {V}}(x,z)$ . Demonstratorul $D$ este modelat ca având putere de calcul nelimitată (în practică, $D$ este de obicei o mașină Turing probabilistică ). Intuitiv, definiția afirmă că un sistem de dovezi interactiv $(D,V)$ este fără divulgare de cunoștințe dacă pentru orice verificator ${\hat {V}}$ există un simulator $S$ eficient (în funcție de ${\hat {V}}$ ) care poate reproduce conversația dintre $D$ și ${\hat {V}}$ pe orice intrare dată. Șirul auxiliar $z$ din definiție joacă rolul de „cunoștințe anterioare” (inclusiv monedele aleatorii ale ${\hat {V}}$ ). Definiția presupune că ${\hat {V}}$ nu poate folosi niciun șir de cunoștințe anterioare $z$ pentru a extrage informații din conversația sa cu $D$ , deoarece dacă simulatorului $S$ i se oferă și această cunoaștere anterioară, atunci acesta poate reproduce conversația dintre ${\hat {V}}$ și $D$ la fel ca înainte.

Definiția dată este cea a noțiunii perfecte de nedivulgare de cunoștințe. Noțiunea computațională de nedivulgare de cunoștințe este obținută prin relaxarea condiției de mai sus, cerând doar ca înregistrările interacțiunilor dintre verificatorului ${\hat {V}}$ și simulatorul nu se pot distinge din punct de vedere computațional, folosind șirul auxiliar.

Exemple practice

Logaritmul discret al unei valori date

De exemplu, dată fiind o valoare $y$ , un număr prim mare $p$ și un generator $g$ , Denisa vrea să demonstreze că știe o valoare $x$ astfel încât $g^{x}{\bmod {p}}=y$ , fără a dezvălui $x$ . Într-adevăr, faptul că Denisa ar cunoaște numărul $x$ ar putea fi folosită ca dovadă a identității, în sensul că Denisa ar putea avea astfel de cunoștințe pentru că a ales o valoare aleatorie $x$ pe care nu a dezvăluit-o nimănui, a calculat $y=g^{x}{\bmod {p}}$ și a distribuit valoarea $y$ tuturor verificatorilor potențiali, astfel încât, ulterior, demonstrarea faptului că știe valoarea lui $x$ să fie echivalent cu a-și demonstra identitatea ca Denisa.

Protocolul decurge după cum urmează: în fiecare rundă, Denisa generează un număr aleatoriu $r$ , calculează $C=g^{r}{\bmod {p}}$ și îi dezvăluie asta lui Victor. După primirea lui $C$ , Victor emite aleatoriu una dintre următoarele două solicitări: fie cere ca Denisa să dezvăluie valoarea $r$ , sau valoarea expresiei $(x+r){\bmod {(p-1)}}$ .

Victor poate verifica oricare dintre răspunsuri; dacă a cerut $r$ , apoi poate calcula valoarea expresiei $g^{r}{\bmod {p}}$ și verifica dacă aceasta este egală cu $C$ . Dacă a cerut $(x+r){\bmod {(p-1)}}$ , poate verifica dacă $C$ este în concordanță cu aceasta, calculând $g^{(x+r){\bmod {(p-1)}}}{\bmod {p}}$ și verificând dacă se valoarea sa este egală cu $(C\cdot y){\bmod {p}}$ . Dacă Denisa știe într-adevăr valoarea $x$ , ea poate răspunde la oricare dintre posibilele provocări ale lui Victor.

Dacă Denisa știa sau ar putea ghici ce provocare va lansa Victor, atunci ar putea să-l înșele cu ușurință și să-l convingă pe Victor că știe $x$ când de fapt nu îl știe: dacă știe că Victor va cere $r$ , apoi procedează normal: ea alege $r$ , calculează $C=g^{r}{\bmod {p}}$ și dezvăluie $C$ lui Victor; ea va putea răspunde provocării lui Victor. Pe de altă parte, dacă știe că Victor va cere $(x+r){\bmod {(p-1)}}$ , apoi alege o valoare aleatorie $r'$ , calculează $C'=g^{r'}\cdot \left(g^{x}\right)^{-1}{\bmod {p}}$ , și dezvăluie $C'$ lui Victor ca valoarea $C$ la care acesta se aștepta. Când Victor o provoacă să dezvăluie $(x+r){\bmod {(p-1)}}$ , ea dezvăluie $r'$ , pentru care Victor va verifica consistența, deoarece va calcula la rândul său $g^{r'}{\bmod {p}}$ , care va fi egală cu $C'\cdot y$ , deoarece Denisa a înmulțit cu inversul multiplicativ modular al lui $y$ .

Totuși, dacă în oricare dintre scenariile de mai sus, Victor lansează o altă provocare decât cea pe care Denisa o aștepta și pentru care a produs rezultatul, atunci ea nu va putea răspunde provocării sub ipoteza infezabilității rezolvării problemei logaritmului discret pentru acest grup. Dacă ea a ales $r$ și a dezvăluit $C=g^{r}{\bmod {p}}$ , atunci ea nu va putea produce un valoare validă $(x+r){\bmod {(p-1)}}$ care ar trece de verificarea lui Victor, în condițiile în care ea nu știe valoarea lui $x$ . Și dacă a ales o valoare $r'$ pe post de $(x+r){\bmod {(p-1)}}$ , ca mai sus, atunci ea ar trebui să răspundă cu logaritmul discret al valorii pe care a dezvăluit-o – dar Denisa nu cunoaște acest logaritm discret, deoarece valoarea C pe care a dezvăluit-o a fost obținută prin aritmetică cu valori cunoscute și nu prin calculul unei puteri cu un exponent cunoscut.

Astfel, un demonstrator trișor are o probabilitate de 0,5 de a trișa cu succes într-o rundă. Prin executarea unui număr suficient de mare de runde, probabilitatea ca un demonstrator trișor să reușească poate fi redusă în mod arbitrar.

Pentru a arăta că demonstrația interactivă de mai sus nu divulgă alte cunoștințe în afară de faptul că Denisa cunoaște valoare lui $x$ , se pot folosi argumente similare cu cele folosite în demonstrația de mai sus a completitudinii și corectitudinii. Mai exact, un simulator, să zicem Simon, care nu cunoaște valoarea lui $x$ , poate simula schimbul de mesaje dintre Denisa și Victor folosind următoarea procedură. În primul rând, Simon dă cu banul folosind o monedă corectă. Dacă rezultatul este „cap”, el alege o valoare aleatorie $r$ , calculează $C=g^{r}{\bmod {p}}$ , și dezvăluie $C$ ca mesaj de la Denisa către Victor. Apoi Simon trimite și un mesaj „cerere valoarea lui $r$ " ca și cum ar fi trimis de la Victor către Denisa și emite imediat valoarea lui $r$ ca mesaj de la Denisa la Victor. O rundă este completă. Pe de altă parte, dacă rezultatul aruncării monedei este „pajură”, Simon alege un număr aleatoriu $r'$ , calculează $C'=g^{r'}\cdot \left(y\right)^{-1}{\bmod {p}}$ , și dezvăluie $C'$ ca mesaj de la Denisa către Victor. Apoi Simon dă „cerere valoarea lui $(x+r){\bmod {(p-1)}}$ " ca mesaj de la Victor către Denisa. În cele din urmă, Simon emite valoarea lui $r'$ ca răspunsul al Denisei către Victor. O rundă este completă. Folosind argumentele anterioare din demonstrațiile completitudinii și corectitudinii, comunicarea interactivă simulată de Simon nu se distinge de adevărata corespondență dintre Denisa și Victor. Proprietatea de nedivulgare de cunoștințe este astfel garantată.

Rezumat

Denisa dovedește că știe valoarea lui x (de exemplu parola ei).

Denisa și Victor cad de acord asupra unui număr prim $p$ și a un generator $g$ al grupului multiplicativ al lui $\mathbb {Z} _{p}$ .
Denisa calculează valoarea expresiei $y=g^{x}{\bmod {p}}$ și i-o trimite lui Victor.
Următorii doi pași se repetă de un număr (mare) de ori.
1. Denisa alege în mod repetat o valoare aleatorie $r\in U[0,p-2]$ și calculează $C=g^{r}{\bmod {p}}$ . Ea îi trimite lui Victor valoarea $C$ .
2. Victor îi cere Denisei să calculeze și să trimită înapoi valoarea $(x+r){\bmod {(p-1)}}$ sau valoarea $r$ . În primul caz Victor verifică $(C\cdot y){\bmod {p}}\equiv g^{(x+r){\bmod {(p-1)}}}{\bmod {p}}$ . În al doilea caz el verifică $C\equiv g^{r}{\bmod {p}}$ .

Valoarea $(x+r){\bmod {(}}p-1)$ poate fi văzută ca valoarea criptată a lui $x{\bmod {(}}p-1)$ . Dacă $r$ este cu adevărat aleatorie, distribuită egal între zero și $(p-2)$ , acest lucru nu scurge nicio informație despre $x$ .

Ciclul hamiltonian pentru un grafic mare

Următoarea schemă se datorează lui Manuel Blum.^[12]

În acest scenariu, Denisa cunoaște un ciclu hamiltonian pentru un graf mare $G$ . Victor cunoaște $G$ dar nu și ciclul (de exemplu, Denisa a generat $G$ și i l-a dezvăluit lui Victor). Se crede că găsirea unui ciclu hamiltonian pentru un graf mare este nefezabilă din punct de vedere computațional, deoarece problema de decizie corespunzătoare este cunoscută ca fiind NP-completă. Denisa va dovedi că știe ciclul fără să-l dezvăluie pur și simplu (poate că Victor este interesat să-l cumpere, dar dorește mai întâi verificarea, sau poate că Denisa este singura care cunoaște aceste informații și își dovedește astfel identitatea lui Victor).

Pentru a arăta că Denisa cunoaște acest ciclu hamiltonian, ea și Victor joacă mai multe runde ale unui joc:

La începutul fiecărei runde, Denisa creează $H$ , un graf izomorf cu $G$ (adică $H$ este la fel ca $G$ , cu excepția faptului că toate vârfurile au nume diferite). Deoarece este trivial să transferăm un ciclu hamiltonian între grafuri izomorfe dat fiind un izomorfism cunoscut, dacă Denisa cunoaște un ciclu hamiltonian pentru $G$ , trebuie să cunoască și unul pentru $H$ .
Denisa își ia un angajament față de alegerea $H$ . Ea ar putea face acest lucru folosind o schemă de angajament criptografic. Alternativ, ea ar putea numerota vârfurile lui $H$ . Apoi, pentru fiecare muchie a grafului $H$ , pe o bucată mică de hârtie, ea notează cele două vârfuri unite de muchie. Apoi pune toate aceste bucăți de hârtie cu fața în jos pe o masă. Scopul acestui angajament este ca Denisa să nu fie capabilă să schimbe $H$ , în timp ce, în același timp, Victor nu are informații despre $H$ .
Victor alege apoi la întâmplare una dintre cele două întrebări pe care să le pună Denisei. El îi poate cere fie să arate izomorfismul dintre $H$ și $G$ , fie îi poate cere să arate un ciclu hamiltonian în $H$ .
Dacă Denisei i se cere să arate că cele două grafuri sunt izomorfe, ea descoperă mai întâi întreg graful $H$ (de exemplu, răsturnând toate bucățile de hârtie pe care le-a pus pe masă) și apoi furnizează translațiile vârfurilor care mapează $G$ la $H$ . Victor poate verifica că acestea sunt într-adevăr izomorfe.
Dacă Denisei i se cere să demonstreze că știe un ciclu hamiltonian în $H$ , ea își translatează ciclul hamiltonian din $G$ în $H$ și descoperă doar muchiile ciclului hamiltonian. Adică, Denisa întoarce doar exact $|V(G)|$ bucăți de hârtie care corespund muchilor ciclului hamiltonian, lăsând restul cu fața în jos. Acest lucru este suficient pentru ca Victor să verifice că $H$ conține într-adevăr un ciclu hamiltonian.

Este important ca angajamentul față de graf să fie astfel încât Victor să poată verifica, în al doilea caz, că ciclul este într-adevăr format din muchii din $H$ . Acest lucru se poate face, de exemplu, luând angajamentul față de fiecare muchie (sau lipsa acesteia) separat.

Completitudine

Dacă Denisa cunoaște un ciclu hamiltonian în $G$ , ea poate satisface cu ușurință cererea lui Victor fie pentru izomorfismul de grafuri care produce $H$ din $G$ (la care s-a angajat în primul pas), fie un ciclu hamiltonian în $H$ (pe care îl poate construi aplicând izomorfismul la ciclul din $G$ ).

Nici o informație suplimentară (zero-knowledge)

Răspunsurile Denisei nu dezvăluie ciclul hamiltonian din graful original $G$ . În fiecare rundă, Victor va învăța doar un izomorfism de la un graf $H$ la $G$ sau un ciclu hamiltonian în $H$ . Ar avea nevoie de ambele răspunsuri pentru un singur $H$ pentru a descoperi ciclul în $G$ , așa că informațiile rămân necunoscute atâta timp cât Denisa poate genera un $H$ distinct în fiecare rundă. Dacă Denisa nu știe despre un ciclu hamiltonian în $G$ , dar știa cumva dinainte ce ar cere Victor să vadă fiecare rundă, atunci ar putea trișa. De exemplu, dacă Denisa știa dinainte că Victor va cere să vadă ciclul hamiltonian în $H$ , atunci ar putea genera un ciclu hamiltonian pentru un grafic fără legătură. În mod similar, dacă Denisa știa dinainte că Victor va cere să vadă izomorfismul, atunci ea ar putea pur și simplu să genereze un graf izomorf $H$ (în care nici ea nu cunoaște un ciclu hamiltonian). Victor ar putea simula protocolul singur (fără Denisa) pentru că știe ce va cere să vadă. Prin urmare, Victor nu obține informații despre ciclul hamiltonian în $G$ din informațiile dezvăluite în fiecare rundă.

Corectitudine

Dacă Denisa nu cunoaște informațiile, ea poate ghici ce întrebare va pune Victor și poate genera fie un graf izomorf cu $G$ , fie un ciclu hamiltonian pentru un graf neînrudit, dar, deoarece nu cunoaște un ciclu hamiltonian pentru $G$ , nu le poate face pe amândouă. Cu această presupunere, șansa ei de a-l păcăli pe Victor este $2 - n$ , unde $n$ este numărul de runde. Este complet nerealist că Denisa ar putea să îl înșele pe Victor în acest fel dat fiind un număr rezonabil de runde.

Variante de nedivulgare de cunoștințe

Diferite variante a ideii de nedivulgare de cunoștințe pot fi definite prin formalizarea conceptului intuitiv a ceea ce se înțelege prin rezultatul produs de simulator „care nu poate fi distins de” execuția reală a protocolului de demonstrație, în următoarele moduri:

Vorbim de nedivulgare de cunoștințe perfectă dacă distribuțiile produse de simulator și protocolul de demonstrare sunt exact la fel. Acesta este, de exemplu, cazul în primul exemplu de mai sus.
Nedivulgare de cunoștințe din punct de vedere statistic^[13] înseamnă că distribuțiile nu sunt neapărat exact aceleași, dar sunt apropiate statistic, ceea ce înseamnă că diferența lor statistică este o funcție neglijabilă.
Vorbim de nedivulgare de cunoștințe din punct de vedere computațional dacă niciun algoritm eficient nu poate distinge cele două distribuții.

Aplicații

Sisteme de autentificare

Cercetarea în domeniul demonstrațiilor fără divulgare de cunoștințe a fost motivată de sistemele de autentificare în care o parte dorește să-și demonstreze identitatea unei alte părți prin intermediul unor informații secrete (cum ar fi o parolă), dar nu dorește ca a doua parte să învețe nimic despre acest secret. Aceasta se numește „dovadă de cunoaștere fără divulgare de cunoștințe”. Cu toate acestea, o parolă este de obicei prea mică sau insuficient aleatorie pentru a fi utilizată în multe scheme pentru dovezi de cunoaștere fără divulgare de cunoștințe.

Dezarmare nucleară

În 2016, Princeton Plasma Physics Laboratory și Princeton University au demonstrat o tehnică care poate avea aplicabilitate la viitoarele discuții privind dezarmarea nucleară. Ar permite inspectorilor să confirme dacă un obiect este într-adevăr o armă nucleară fără a înregistra, împărtăși sau dezvălui funcționarea internă care ar putea fi secretă.^[14]

Blockchain-uri

Demonstrațiile fără divulgare de cunoștințe au fost aplicate în protocoalele Zerocoin și Zerocash, care au culminat cu nașterea Zcoin^[15] (care și-a schimbat numele în Firo în 2020, în urma unui proces de rebranding)^[16] și criptomonedele Zcash în 2016.

În 2018, au fost introduse Bulletproofs. Bulletproofs reprezintă o îmbunătățire față de demonstrațiile ne-interactive fără divulgare de cunoștințe, în care nu este necesară încrederea într-o configurare inițială.^[17] Ulterior aceste idei au fost implementate în protocolul Mimblewimble (pe care se bazează criptomonedele Grin și Beam) și criptomoneda Monero.^[18]

Istorie

Demonstrațiile fără divulgare de cunoștințe au fost concepute pentru prima dată în 1985 de Shafi Goldwasser, Silvio Micali și Charles Rackoff în lucrarea lor „The Knowledge Complexity of Interactive Proof-Systems”.^[19] Această lucrare a introdus ierarhia IP a sistemelor interactive de deducție și conceptul de complexitate a cunoștințelor, o măsură a cantității de cunoștințe despre o demonstrație care se scurg de la demonstrator către verificator. Ei au dat, de asemenea, prima demonstrație fără divulgare de cunoștințe pentru o problemă concretă, aceea de a decide non-reziduurile pătratice modulo m. Împreună cu o lucrare a lui László Babai și Shlomo Moran, această lucrare emblematică a inventat sisteme interactive de deducție, pentru care toți cei cinci autori au câștigat primul premiu Gödel în 1993.

O altă variantă a demonstrațiilor fără divulgare de cunoștințe sunt demonstrațiile non-interactive fără divulgare de cunoștințe. Blum, Feldman și Micali au arătat că un șir aleatoriu comun împărțit între demonstrator și verificator este suficient pentru a obține nedivulgare de cunoștințe din punct de vedere computațional fără a necesita interacțiune.^[5]^[6]

Protocoale de demonstrare fără divulgare de cunoștințe

Cele mai populare protocoale interactive sau non-interactive de demonstrare fără divulgare de cunoștințe (de exemplu, zk-SNARK) pot fi clasificate în linii mari în următoarele patru categorii: argumente de cunoaștere succinte non-interactive (SNARK), argumente de cunoaștere transparente scalabile (STARK), Delegare polinomială verificabilă (VPD) și argumente succinte non-interactive (SNARG). O listă de protocoale și biblioteci de demonstrare fără divulgare de cunoștințe este furnizată mai jos, împreună cu comparații bazate pe transparență, universalitate, securitate post-cuantică plauzibilă și paradigmă de programare.^[20] Un protocol transparent este unul care nu necesită nicio configurare inițială de încredere și folosește surse publice pentru generarea numerelor aleatoare. Un protocol universal este unul care nu necesită o configurare de încredere separată pentru fiecare circuit. În cele din urmă, un protocol post-cuantic plauzibil este unul care nu este susceptibil la atacuri cunoscute care implică algoritmi cuantici.

Sisteme de demonstrare fără divulgare de cunoștințe
ZKP System	Publication year	Protocol	Transparent	Universal	Plauzibil sigur post-quantum	Paradigma de programare
Pinocchio^[21]	2013	zk-SNARK	Nu	Nu	Nu	Procedural
Geppetto^[22]	2015	zk-SNARK	Nu	Nu	Nu	Procedural
TinyRAM^[23]	2013	zk-SNARK	Nu	Nu	Nu	Procedural
Buffet^[24]	2015	zk-SNARK	Nu	Nu	Nu	Procedural
ZoKrates^[25]	2018	zk-SNARK	Nu	Nu	Nu	Procedural
xJsnark^[26]	2018	zk-SNARK	Nu	Nu	Nu	Procedural
vRAM^[27]	2018	zk-SNARG	Nu	Da	Nu	Limbaj de asamblare
vnTinyRAM^[28]	2014	zk-SNARK	Nu	Da	Nu	Procedural
MIRAGE^[29]	2020	zk-SNARK	Nu	Da	Nu	Circuite aritmetice
Sonic^[30]	2019	zk-SNARK	Nu	Da	Nu	Circuite aritmetice
Marlin^[31]	2020	zk-SNARK	Nu	Da	Nu	Circuite aritmetice
PLONK^[32]	2019	zk-SNARK	Nu	Da	Nu	Circuite aritmetice
SuperSonic^[33]	2020	zk-SNARK	Da	Da	Nu	Circuite aritmetice
Bulletproofs^[34]	2018	Bulletproofs	Da	Da	Nu	Circuite aritmetice
Hyrax^[35]	2018	zk-SNARK	Da	Da	Nu	Circuite aritmetice
Halo^[36]	2019	zk-SNARK	Da	Da	Nu	Circuite aritmetice
Virgo^[37]	2020	zk-SNARK	Da	Da	Da	Circuite aritmetice
Ligero^[38]	2017	zk-SNARK	Da	Da	Da	Circuite aritmetice
Aurora^[39]	2019	zk-SNARK	Da	Da	Da	Circuite aritmetice
zk-STARK^[40]	2019	zk-STARK	Da	Da	Da	Limbaj de asamblare
Zilch^[41]	2021	zk-STARK	Da	Da	Da	Orientat obiecte

Note

^ Aad, Imad (2023), Mulder, Valentin; Mermoud, Alain; Lenders, Vincent; Tellenbach, Bernhard, ed., „Zero-Knowledge Proof”, Trends in Data Protection and Encryption Technologies (în engleză), Cham: Springer Nature Switzerland, pp. 25–30, doi:10.1007/978-3-031-33386-6_6 , ISBN 978-3-031-33386-6, accesat în 13 octombrie 2023
^ Goldreich, Oded (2001). Foundations of Cryptography Volume I. Cambridge University Press. p. 184. doi:10.1017/CBO9780511546891. ISBN 9780511546891.
^ Goldreich, Oded (2001). Foundations of Cryptography Volume I. Cambridge University Press. p. 247. doi:10.1017/CBO9780511546891. ISBN 9780511546891.
^ Goldreich, Oded (2001). Foundations of Cryptography Volume I. Cambridge University Press. p. 299. doi:10.1017/CBO9780511546891. ISBN 9780511546891.
^ ^a ^b Blum, Manuel; Feldman, Paul; Micali, Silvio (1988). „Non-interactive zero-knowledge and its applications”. Proceedings of the twentieth annual ACM symposium on Theory of computing - STOC '88 (PDF). pp. 103–112. doi:10.1145/62212.62222. ISBN 978-0897912648. Accesat în 2 iunie 2022. Mentenanță CS1: Dată și an (link)
^ ^a ^b Wu, Huixin; Wang, Feng (2014). „A Survey of Noninteractive Zero Knowledge Proof System and Its Applications”. The Scientific World Journal. 2014: 560484. doi:10.1155/2014/560484. PMC 4032740 . PMID 24883407.
^ Quisquater, Jean-Jacques; Guillou, Louis C.; Berson, Thomas A. (1990). „How to Explain Zero-Knowledge Protocols to Your Children”. Advances in Cryptology — CRYPTO' 89 Proceedings (PDF). Lecture Notes in Computer Science. 435. pp. 628–631. doi:10.1007/0-387-34805-0_60. ISBN 978-0-387-97317-3.
^ Chalkias, Konstantinos. „Demonstrate how Zero-Knowledge Proofs work without using maths”. CordaCon 2017 (în engleză). Accesat în 13 septembrie 2017.
^ ^a ^b ^c Murtagh, Jack (1 iulie 2023). „Where's Waldo? How to Mathematically Prove You Found Him without Revealing Where He Is”. Scientific American. Accesat în 2 octombrie 2023.
^ Gradwohl, Ronen; Naor, Moni; Pinkas, Benny; Rothblum, Guy N. (2009). „Cryptographic and Physical Zero-Knowledge Proof Systems for Solutions of Sudoku Puzzles” (PDF). Theory Comput. Syst. 44 (2): 245 – 268. doi:10.1007/978-3-540-72914-3_16.
^ Feige, Uriel; Fiat, Amos; Shamir, Adi (1 iunie 1988). „Zero-knowledge proofs of identity”. Journal of Cryptology (în engleză). 1 (2): 77–94. doi:10.1007/BF02351717. ISSN 1432-1378.
^ Blum, Manuel (1986). „How to Prove a Theorem So No One Else Can Claim It” (PDF). ICM Proceedings: 1444–1451. Arhivat din original (PDF) la 3 ianuarie 2023.
^ Sahai, Amit; Vadhan, Salil (1 martie 2003). „A complete problem for statistical zero knowledge” (PDF). Journal of the ACM. 50 (2): 196–249. doi:10.1145/636865.636868. Arhivat din original (PDF) la 25 iunie 2015.
^ „PPPL and Princeton demonstrate novel technique that may have applicability to future nuclear disarmament talks - Princeton Plasma Physics Lab”. www.pppl.gov. Arhivat din original la 3 iulie 2017.
^ Hellwig, Daniel; Karlic, Goran; Huchzermeier, Arnd (3 mai 2020). „Privacy and Anonymity”. Build Your Own Blockchain. Management for Professionals. SpringerLink. p. 112. doi:10.1007/978-3-030-40142-9_5. ISBN 9783030401429. Accesat în 3 decembrie 2020.
^ Hurst, Samantha (28 octombrie 2020). „Zcoin Announces Rebranding to New Name & Ticker "Firo"”. Crowdfund Insider. Arhivat din original la 1 noiembrie 2020. Accesat în 4 noiembrie 2020.
^ Bünz, B; Bootle, D; Boneh, A (2018). „Bulletproofs: Short Proofs for Confidential Transactions and More”. 2018 IEEE Symposium on Security and Privacy (SP). San Francisco, California. pp. 315–334. doi:10.1109/SP.2018.00020. ISBN 978-1-5386-4353-2.
^ Odendaal, Hansie; Sharrock, Cayle; Heerden, SW. „Bulletproofs and Mimblewimble”. Tari Labs University. Arhivat din original la 29 septembrie 2020. Accesat în 3 decembrie 2020.
^ Goldwasser, S.; Micali, S.; Rackoff, C. (1989), „The knowledge complexity of interactive proof systems” (PDF), SIAM Journal on Computing, 18 (1), pp. 186–208, doi:10.1137/0218012, ISSN 1095-7111
^ Mouris, Dimitris; Tsoutsos, Nektarios Georgios (2021). „Zilch: A Framework for Deploying Transparent Zero-Knowledge Proofs”. IEEE Transactions on Information Forensics and Security. 16: 3269–3284. doi:10.1109/TIFS.2021.3074869. ISSN 1556-6021.
^ Parno, B.; Howell, J.; Gentry, C.; Raykova, M. (mai 2013). „Pinocchio: Nearly Practical Verifiable Computation”. 2013 IEEE Symposium on Security and Privacy. pp. 238–252. doi:10.1109/SP.2013.47. ISBN 978-0-7695-4977-4.
^ Costello, Craig; Fournet, Cedric; Howell, Jon; Kohlweiss, Markulf; Kreuter, Benjamin; Naehrig, Michael; Parno, Bryan; Zahur, Samee (mai 2015). „Geppetto: Versatile Verifiable Computation”. 2015 IEEE Symposium on Security and Privacy. pp. 253–270. doi:10.1109/SP.2015.23. hdl:20.500.11820/37920e55-65aa-4a42-b678-ef5902a5dd45 . ISBN 978-1-4673-6949-7.
^ Ben-Sasson, Eli; Chiesa, Alessandro; Genkin, Daniel; Tromer, Eran; Virza, Madars (2013). „SNARKs for C: Verifying Program Executions Succinctly and in Zero Knowledge”. Advances in Cryptology – CRYPTO 2013. Lecture Notes in Computer Science. 8043. pp. 90–108. doi:10.1007/978-3-642-40084-1_6. hdl:1721.1/87953 . ISBN 978-3-642-40083-4.
^ Wahby, Riad S.; Setty, Srinath; Ren, Zuocheng; Blumberg, Andrew J.; Walfish, Michael (2015). „Efficient RAM and Control Flow in Verifiable Outsourced Computation”. Proceedings 2015 Network and Distributed System Security Symposium. doi:10.14722/ndss.2015.23097. ISBN 978-1-891562-38-9.
^ Eberhardt, Jacob; Tai, Stefan (iulie 2018). „ZoKrates - Scalable Privacy-Preserving Off-Chain Computations”. 2018 IEEE International Conference on Internet of Things (IThings) and IEEE Green Computing and Communications (GreenCom) and IEEE Cyber, Physical and Social Computing (CPSCom) and IEEE Smart Data (SmartData). pp. 1084–1091. doi:10.1109/Cybermatics_2018.2018.00199. ISBN 978-1-5386-7975-3.
^ Kosba, Ahmed; Papamanthou, Charalampos; Shi, Elaine (mai 2018). „XJsnark: A Framework for Efficient Verifiable Computation”. 2018 IEEE Symposium on Security and Privacy (SP). pp. 944–961. doi:10.1109/SP.2018.00018 . ISBN 978-1-5386-4353-2.
^ Zhang, Yupeng; Genkin, Daniel; Katz, Jonathan; Papadopoulos, Dimitrios; Papamanthou, Charalampos (mai 2018). „VRAM: Faster Verifiable RAM with Program-Independent Preprocessing”. 2018 IEEE Symposium on Security and Privacy (SP). pp. 908–925. doi:10.1109/SP.2018.00013 . ISBN 978-1-5386-4353-2.
^ Ben-Sasson, Eli; Chiesa, Alessandro; Tromer, Eran; Virza, Madars (20 august 2014). „Succinct non-interactive zero knowledge for a von Neumann architecture”. Proceedings of the 23rd USENIX Conference on Security Symposium. USENIX Association: 781–796. ISBN 9781931971157.
^ Kosba, Ahmed; Papadopoulos, Dimitrios; Papamanthou, Charalampos; Song, Dawn (2020). „MIRAGE: Succinct Arguments for Randomized Algorithms with Applications to Universal zk-SNARKs”. Cryptology ePrint Archive.
^ Maller, Mary; Bowe, Sean; Kohlweiss, Markulf; Meiklejohn, Sarah (6 noiembrie 2019). „Sonic: Zero-Knowledge SNARKs from Linear-Size Universal and Updatable Structured Reference Strings”. Proceedings of the 2019 ACM SIGSAC Conference on Computer and Communications Security. Association for Computing Machinery. pp. 2111–2128. doi:10.1145/3319535.3339817. hdl:20.500.11820/739b94f1-54f0-4ec3-9644-3c95eea1e8f5 . ISBN 9781450367479.
^ Chiesa, Alessandro; Hu, Yuncong; Maller, Mary; Mishra, Pratyush; Vesely, Noah; Ward, Nicholas (2020). „Marlin: Preprocessing zkSNARKs with Universal and Updatable SRS”. Advances in Cryptology – EUROCRYPT 2020. Lecture Notes in Computer Science (în engleză). 12105. Springer International Publishing. pp. 738–768. doi:10.1007/978-3-030-45721-1_26. ISBN 978-3-030-45720-4.
^ Gabizon, Ariel; Williamson, Zachary J.; Ciobotaru, Oana (2019). „PLONK: Permutations over Lagrange-bases for Oecumenical Noninteractive arguments of Knowledge”. Cryptology ePrint Archive.
^ Bünz, Benedikt; Fisch, Ben; Szepieniec, Alan (2020). „Transparent SNARKs from DARK Compilers”. Advances in Cryptology – EUROCRYPT 2020. Lecture Notes in Computer Science (în engleză). 12105. Springer International Publishing. pp. 677–706. doi:10.1007/978-3-030-45721-1_24. ISBN 978-3-030-45720-4.
^ Bünz, B; Bootle, D; Boneh, A (2018). „Bulletproofs: Short Proofs for Confidential Transactions and More”. 2018 IEEE Symposium on Security and Privacy (SP). San Francisco, California. pp. 315–334. doi:10.1109/SP.2018.00020 . ISBN 978-1-5386-4353-2.
^ Wahby, Riad S.; Tzialla, Ioanna; Shelat, Abhi; Thaler, Justin; Walfish, Michael (mai 2018). „Doubly-Efficient zkSNARKs Without Trusted Setup”. 2018 IEEE Symposium on Security and Privacy (SP). pp. 926–943. doi:10.1109/SP.2018.00060 . ISBN 978-1-5386-4353-2.
^ Bowe, Sean; Grigg, Jack; Hopwood, Daira (2019). „Recursive Proof Composition without a Trusted Setup”. Cryptology ePrint Archive.
^ Zhang, Jiaheng; Xie, Tiancheng; Zhang, Yupeng; Song, Dawn (mai 2020). „Transparent Polynomial Delegation and Its Applications to Zero Knowledge Proof”. 2020 IEEE Symposium on Security and Privacy (SP). pp. 859–876. doi:10.1109/SP40000.2020.00052 . ISBN 978-1-7281-3497-0.
^ Ames, Scott; Hazay, Carmit; Ishai, Yuval; Venkitasubramaniam, Muthuramakrishnan (30 octombrie 2017). „Ligero”. Proceedings of the 2017 ACM SIGSAC Conference on Computer and Communications Security. Association for Computing Machinery. pp. 2087–2104. doi:10.1145/3133956.3134104. ISBN 9781450349468.
^ Ben-Sasson, Eli; Chiesa, Alessandro; Riabzev, Michael; Spooner, Nicholas; Virza, Madars; Ward, Nicholas P. (2019). „Aurora: Transparent Succinct Arguments for R1CS”. Advances in Cryptology – EUROCRYPT 2019. Lecture Notes in Computer Science (în engleză). 11476. Springer International Publishing. pp. 103–128. doi:10.1007/978-3-030-17653-2_4. ISBN 978-3-030-17652-5.
^ Ben-Sasson, Eli; Bentov, Iddo; Horesh, Yinon; Riabzev, Michael (2019). „Scalable Zero Knowledge with No Trusted Setup”. Advances in Cryptology – CRYPTO 2019. Lecture Notes in Computer Science (în engleză). 11694. Springer International Publishing. pp. 701–732. doi:10.1007/978-3-030-26954-8_23. ISBN 978-3-030-26953-1.
^ Mouris, Dimitris; Tsoutsos, Nektarios Georgios (2021). „Zilch: A Framework for Deploying Transparent Zero-Knowledge Proofs”. IEEE Transactions on Information Forensics and Security. 16: 3269–3284. doi:10.1109/TIFS.2021.3074869. ISSN 1556-6021.

[1] Aad, Imad (2023), Mulder, Valentin; Mermoud, Alain; Lenders, Vincent; Tellenbach, Bernhard, ed., „Zero-Knowledge Proof”, Trends in Data Protection and Encryption Technologies (în engleză), Cham: Springer Nature Switzerland, pp. 25–30, doi:10.1007/978-3-031-33386-6_6 , ISBN 978-3-031-33386-6, accesat în 13 octombrie 2023

[2] Goldreich, Oded (2001). Foundations of Cryptography Volume I. Cambridge University Press. p. 184. doi:10.1017/CBO9780511546891. ISBN 9780511546891.

[3] Goldreich, Oded (2001). Foundations of Cryptography Volume I. Cambridge University Press. p. 247. doi:10.1017/CBO9780511546891. ISBN 9780511546891.

[4] Goldreich, Oded (2001). Foundations of Cryptography Volume I. Cambridge University Press. p. 299. doi:10.1017/CBO9780511546891. ISBN 9780511546891.

[noninteractive-5] Blum, Manuel; Feldman, Paul; Micali, Silvio (1988). „Non-interactive zero-knowledge and its applications”. Proceedings of the twentieth annual ACM symposium on Theory of computing - STOC '88 (PDF). pp. 103–112. doi:10.1145/62212.62222. ISBN 978-0897912648. Accesat în 2 iunie 2022. Mentenanță CS1: Dată și an (link)

[noninteractive2-6] Wu, Huixin; Wang, Feng (2014). „A Survey of Noninteractive Zero Knowledge Proof System and Its Applications”. The Scientific World Journal. 2014: 560484. doi:10.1155/2014/560484. PMC 4032740 . PMID 24883407.

[7] Quisquater, Jean-Jacques; Guillou, Louis C.; Berson, Thomas A. (1990). „How to Explain Zero-Knowledge Protocols to Your Children”. Advances in Cryptology — CRYPTO' 89 Proceedings (PDF). Lecture Notes in Computer Science. 435. pp. 628–631. doi:10.1007/0-387-34805-0_60. ISBN 978-0-387-97317-3.

[8] Chalkias, Konstantinos. „Demonstrate how Zero-Knowledge Proofs work without using maths”. CordaCon 2017 (în engleză). Accesat în 13 septembrie 2017.

[Murtagh-9] Murtagh, Jack (1 iulie 2023). „Where's Waldo? How to Mathematically Prove You Found Him without Revealing Where He Is”. Scientific American. Accesat în 2 octombrie 2023.

[10] Gradwohl, Ronen; Naor, Moni; Pinkas, Benny; Rothblum, Guy N. (2009). „Cryptographic and Physical Zero-Knowledge Proof Systems for Solutions of Sudoku Puzzles” (PDF). Theory Comput. Syst. 44 (2): 245 – 268. doi:10.1007/978-3-540-72914-3_16.

[11] Feige, Uriel; Fiat, Amos; Shamir, Adi (1 iunie 1988). „Zero-knowledge proofs of identity”. Journal of Cryptology (în engleză). 1 (2): 77–94. doi:10.1007/BF02351717. ISSN 1432-1378.

[blum86-12] Blum, Manuel (1986). „How to Prove a Theorem So No One Else Can Claim It” (PDF). ICM Proceedings: 1444–1451. Arhivat din original (PDF) la 3 ianuarie 2023.

[13] Sahai, Amit; Vadhan, Salil (1 martie 2003). „A complete problem for statistical zero knowledge” (PDF). Journal of the ACM. 50 (2): 196–249. doi:10.1145/636865.636868. Arhivat din original (PDF) la 25 iunie 2015.

[14] „PPPL and Princeton demonstrate novel technique that may have applicability to future nuclear disarmament talks - Princeton Plasma Physics Lab”. www.pppl.gov. Arhivat din original la 3 iulie 2017.

[Hellwig_2020-15] Hellwig, Daniel; Karlic, Goran; Huchzermeier, Arnd (3 mai 2020). „Privacy and Anonymity”. Build Your Own Blockchain. Management for Professionals. SpringerLink. p. 112. doi:10.1007/978-3-030-40142-9_5. ISBN 9783030401429. Accesat în 3 decembrie 2020.

[16] Hurst, Samantha (28 octombrie 2020). „Zcoin Announces Rebranding to New Name & Ticker "Firo"”. Crowdfund Insider. Arhivat din original la 1 noiembrie 2020. Accesat în 4 noiembrie 2020.

[Bulletproofs-17] Bünz, B; Bootle, D; Boneh, A (2018). „Bulletproofs: Short Proofs for Confidential Transactions and More”. 2018 IEEE Symposium on Security and Privacy (SP). San Francisco, California. pp. 315–334. doi:10.1109/SP.2018.00020. ISBN 978-1-5386-4353-2.

[18] Odendaal, Hansie; Sharrock, Cayle; Heerden, SW. „Bulletproofs and Mimblewimble”. Tari Labs University. Arhivat din original la 29 septembrie 2020. Accesat în 3 decembrie 2020.

[knowledgecomplexity-19] Goldwasser, S.; Micali, S.; Rackoff, C. (1989), „The knowledge complexity of interactive proof systems” (PDF), SIAM Journal on Computing, 18 (1), pp. 186–208, doi:10.1137/0218012, ISSN 1095-7111

[mouris21-20] Mouris, Dimitris; Tsoutsos, Nektarios Georgios (2021). „Zilch: A Framework for Deploying Transparent Zero-Knowledge Proofs”. IEEE Transactions on Information Forensics and Security. 16: 3269–3284. doi:10.1109/TIFS.2021.3074869. ISSN 1556-6021.

[21] Parno, B.; Howell, J.; Gentry, C.; Raykova, M. (mai 2013). „Pinocchio: Nearly Practical Verifiable Computation”. 2013 IEEE Symposium on Security and Privacy. pp. 238–252. doi:10.1109/SP.2013.47. ISBN 978-0-7695-4977-4.

[22] Costello, Craig; Fournet, Cedric; Howell, Jon; Kohlweiss, Markulf; Kreuter, Benjamin; Naehrig, Michael; Parno, Bryan; Zahur, Samee (mai 2015). „Geppetto: Versatile Verifiable Computation”. 2015 IEEE Symposium on Security and Privacy. pp. 253–270. doi:10.1109/SP.2015.23. hdl:20.500.11820/37920e55-65aa-4a42-b678-ef5902a5dd45 . ISBN 978-1-4673-6949-7.

[23] Ben-Sasson, Eli; Chiesa, Alessandro; Genkin, Daniel; Tromer, Eran; Virza, Madars (2013). „SNARKs for C: Verifying Program Executions Succinctly and in Zero Knowledge”. Advances in Cryptology – CRYPTO 2013. Lecture Notes in Computer Science. 8043. pp. 90–108. doi:10.1007/978-3-642-40084-1_6. hdl:1721.1/87953 . ISBN 978-3-642-40083-4.

[24] Wahby, Riad S.; Setty, Srinath; Ren, Zuocheng; Blumberg, Andrew J.; Walfish, Michael (2015). „Efficient RAM and Control Flow in Verifiable Outsourced Computation”. Proceedings 2015 Network and Distributed System Security Symposium. doi:10.14722/ndss.2015.23097. ISBN 978-1-891562-38-9.

[25] Eberhardt, Jacob; Tai, Stefan (iulie 2018). „ZoKrates - Scalable Privacy-Preserving Off-Chain Computations”. 2018 IEEE International Conference on Internet of Things (IThings) and IEEE Green Computing and Communications (GreenCom) and IEEE Cyber, Physical and Social Computing (CPSCom) and IEEE Smart Data (SmartData). pp. 1084–1091. doi:10.1109/Cybermatics_2018.2018.00199. ISBN 978-1-5386-7975-3.

[26] Kosba, Ahmed; Papamanthou, Charalampos; Shi, Elaine (mai 2018). „XJsnark: A Framework for Efficient Verifiable Computation”. 2018 IEEE Symposium on Security and Privacy (SP). pp. 944–961. doi:10.1109/SP.2018.00018 . ISBN 978-1-5386-4353-2.

[27] Zhang, Yupeng; Genkin, Daniel; Katz, Jonathan; Papadopoulos, Dimitrios; Papamanthou, Charalampos (mai 2018). „VRAM: Faster Verifiable RAM with Program-Independent Preprocessing”. 2018 IEEE Symposium on Security and Privacy (SP). pp. 908–925. doi:10.1109/SP.2018.00013 . ISBN 978-1-5386-4353-2.

[28] Ben-Sasson, Eli; Chiesa, Alessandro; Tromer, Eran; Virza, Madars (20 august 2014). „Succinct non-interactive zero knowledge for a von Neumann architecture”. Proceedings of the 23rd USENIX Conference on Security Symposium. USENIX Association: 781–796. ISBN 9781931971157.

[29] Kosba, Ahmed; Papadopoulos, Dimitrios; Papamanthou, Charalampos; Song, Dawn (2020). „MIRAGE: Succinct Arguments for Randomized Algorithms with Applications to Universal zk-SNARKs”. Cryptology ePrint Archive.

[30] Maller, Mary; Bowe, Sean; Kohlweiss, Markulf; Meiklejohn, Sarah (6 noiembrie 2019). „Sonic: Zero-Knowledge SNARKs from Linear-Size Universal and Updatable Structured Reference Strings”. Proceedings of the 2019 ACM SIGSAC Conference on Computer and Communications Security. Association for Computing Machinery. pp. 2111–2128. doi:10.1145/3319535.3339817. hdl:20.500.11820/739b94f1-54f0-4ec3-9644-3c95eea1e8f5 . ISBN 9781450367479.

[31] Chiesa, Alessandro; Hu, Yuncong; Maller, Mary; Mishra, Pratyush; Vesely, Noah; Ward, Nicholas (2020). „Marlin: Preprocessing zkSNARKs with Universal and Updatable SRS”. Advances in Cryptology – EUROCRYPT 2020. Lecture Notes in Computer Science (în engleză). 12105. Springer International Publishing. pp. 738–768. doi:10.1007/978-3-030-45721-1_26. ISBN 978-3-030-45720-4.

[32] Gabizon, Ariel; Williamson, Zachary J.; Ciobotaru, Oana (2019). „PLONK: Permutations over Lagrange-bases for Oecumenical Noninteractive arguments of Knowledge”. Cryptology ePrint Archive.

[33] Bünz, Benedikt; Fisch, Ben; Szepieniec, Alan (2020). „Transparent SNARKs from DARK Compilers”. Advances in Cryptology – EUROCRYPT 2020. Lecture Notes in Computer Science (în engleză). 12105. Springer International Publishing. pp. 677–706. doi:10.1007/978-3-030-45721-1_24. ISBN 978-3-030-45720-4.

[Bulletproofs2-34] Bünz, B; Bootle, D; Boneh, A (2018). „Bulletproofs: Short Proofs for Confidential Transactions and More”. 2018 IEEE Symposium on Security and Privacy (SP). San Francisco, California. pp. 315–334. doi:10.1109/SP.2018.00020 . ISBN 978-1-5386-4353-2.

[35] Wahby, Riad S.; Tzialla, Ioanna; Shelat, Abhi; Thaler, Justin; Walfish, Michael (mai 2018). „Doubly-Efficient zkSNARKs Without Trusted Setup”. 2018 IEEE Symposium on Security and Privacy (SP). pp. 926–943. doi:10.1109/SP.2018.00060 . ISBN 978-1-5386-4353-2.

[36] Bowe, Sean; Grigg, Jack; Hopwood, Daira (2019). „Recursive Proof Composition without a Trusted Setup”. Cryptology ePrint Archive.

[37] Zhang, Jiaheng; Xie, Tiancheng; Zhang, Yupeng; Song, Dawn (mai 2020). „Transparent Polynomial Delegation and Its Applications to Zero Knowledge Proof”. 2020 IEEE Symposium on Security and Privacy (SP). pp. 859–876. doi:10.1109/SP40000.2020.00052 . ISBN 978-1-7281-3497-0.

[38] Ames, Scott; Hazay, Carmit; Ishai, Yuval; Venkitasubramaniam, Muthuramakrishnan (30 octombrie 2017). „Ligero”. Proceedings of the 2017 ACM SIGSAC Conference on Computer and Communications Security. Association for Computing Machinery. pp. 2087–2104. doi:10.1145/3133956.3134104. ISBN 9781450349468.

[39] Ben-Sasson, Eli; Chiesa, Alessandro; Riabzev, Michael; Spooner, Nicholas; Virza, Madars; Ward, Nicholas P. (2019). „Aurora: Transparent Succinct Arguments for R1CS”. Advances in Cryptology – EUROCRYPT 2019. Lecture Notes in Computer Science (în engleză). 11476. Springer International Publishing. pp. 103–128. doi:10.1007/978-3-030-17653-2_4. ISBN 978-3-030-17652-5.

[40] Ben-Sasson, Eli; Bentov, Iddo; Horesh, Yinon; Riabzev, Michael (2019). „Scalable Zero Knowledge with No Trusted Setup”. Advances in Cryptology – CRYPTO 2019. Lecture Notes in Computer Science (în engleză). 11694. Springer International Publishing. pp. 701–732. doi:10.1007/978-3-030-26954-8_23. ISBN 978-3-030-26953-1.

[mouris212-41] Mouris, Dimitris; Tsoutsos, Nektarios Georgios (2021). „Zilch: A Framework for Deploying Transparent Zero-Knowledge Proofs”. IEEE Transactions on Information Forensics and Security. 16: 3269–3284. doi:10.1109/TIFS.2021.3074869. ISSN 1556-6021.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

[21]

[22]

[23]

[24]

[25]

[26]

[27]

[28]

[29]

[30]

[31]

[32]

[33]

[34]

[35]

[36]

[37]

[38]

[39]

[40]

[41]