Bitangente ale unei cuartice

Curba Trott (neagră) are 28 de bitangente (roșii). Imaginea prezintă 7 dintre ele; celelalte sunt simetrice la rotațiile de 90° față de origine și reflexiile față de cele două axe albastre.

Curba Trott cu toate cele 28 de bitangente

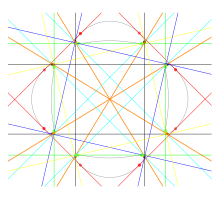
În teoria curbelor plane algebrice, o cuartică plană generală are 28 de bitangente, drepte care sunt tangente la curbă în două locuri. Aceste drepte există în planul proiectiv complex, dar este posibil să se definească curbe cuartice pentru care toate cele 28 de linii au drept coordonate numere reale și care, prin urmare, aparțin planului euclidian.

O cuartică explicită cu douăzeci și opt de bitangente reale a fost găsită mai întâi de (Plücker 1839) După cum a arătat Plücker, numărul de bitangente reale ai oricărei cuartice trebuie să fie 28, 16 sau un număr mai mic decât 9. O altă cuartică cu 28 de bitangente reale poate fi formată din locul geometric al centrelor elipselor cu lungimi fixe ale axei, tangente la două drepte neparalele. Shioda (1995) a dat o construcție diferită a unei cuartice cu douăzeci și opt de bitangente, formată prin proiectarea unei suprafețe cubice; douăzeci și șapte dintre bitangentele curbei lui Shioda sunt reale, în timp ce a douăzeci și opta este dreapta de la infinit în planul proiectiv^⁠(d).

Exemplu

Curba Trott, o altă curbă cu 28 de bitangente reale, este mulțimea de puncte (x,y) care satisface ecuația polinomială de gradul patru

$\displaystyle 144(x^{4}+y^{4})-225(x^{2}+y^{2})+350x^{2}y^{2}+81=0.$

Aceste puncte formează o curbă cuartică nesingulară de genul trei și care are douăzeci și opt de bitangente reale.

Ca și exemplele lui Plücker și ale lui Blum și Guinand, curba Trott are patru ovale separate, numărul maxim pentru o curbă de gradul patru, ca urmare este o curbă M^⁠(d). Cele patru ovale pot fi grupate în perechi în șase moduri diferite; pentru fiecare pereche de ovale există patru bitangente care ating ambele ovale din pereche, două care separă cele două ovale (în semiplane diferite) și două care nu. În plus, fiecare oval delimitează o regiune neconvexă a planului și are o bitangentă la porțiunea neconvexă a frontierei sale.

Conexiuni cu alte structuri

Curba duală^⁠(d) la o curbă cuartică are 28 de puncte duble obișnuite reale, duale la cele 28 de bitangente ale curbei primare.

Cele 28 de bitangente ale unei cuartice pot fi puse în corespondență cu simbolurile formei

$\left[{\begin{array}{ccc}a&b&c\\d&e&f\\\end{array}}\right]$

unde a, b, c, d, e și f sunt toate 0 sau 1 și unde

$ad+be+cf=1(\mod 2).$

Există 64 de posibilități pentru a, b, c, d, e și f, dar numai 28 dintre acestea produc o sumă impară. De asemenea, a, b și c pot fi interpretate drept coordonatele omogene ale unui punct din planul orientat Fano iar d, e și f drept coordonatele unei drepte în același plan proiectiv finit. Condiția ca suma să fie impară este echivalentă cu necesitatea ca punctul și linia să nu se atingă și există 28 de perechi diferite de punct și dreaptă care nu se ating.

Punctele și dreptele din planul Fano care sunt disjuncte dintr-o pereche punct și dreaptă neincidentă formează un triunghi, iar bitangentele unei cuartice au fost considerate ca fiind în corespondență cu cele 28 de triunghiuri ale planului Fano. Graful Levi al planului Fano este graful Heawood, în care triunghiurile din planul Fano sunt reprezentate de cicluri cu 6 noduri. Cele 28 de cicluri cu 6 noduri ale grafului Heawood corespund, la rândul lor, celor 28 de vârfuri ale grafului Coxeter.

Cele 28 de bitangente ale unei cuartice corespund și perechilor de 56 de drepte de pe o suprafață del Pezzo de gradul 2 și celor 28 de caracteristici theta. impare.

Cele 27 de drepte ale unei cubice și cele 28 de bitangente ale unei cuartice, împreună cu cele 120 de plane tritangente ale unei curbe sextice canonice de genul 4 formează o „trinitate” în sensul lui Vladimir Arnold, în special o formă de corespondență McKay, și pot fi legate de multe alte obiecte matematice.

Bibliografie

• en Blum, R.; Guinand, A. P. (1964). „A quartic with 28 real bitangents”. Canadian Mathematical Bulletin. 7 (3): 399–404. doi:10.4153/cmb-1964-038-6 . 
• en Cayley, Arthur (1879), „On the bitangents of a quartic”, Salmon's Higher Plane Curves, pp. 387–389 . In The collected mathematical papers of Arthur Cayley, Andrew Russell Forsyth, ed., The University Press, 1896, vol. 11, pp. 221–223
• en Gray, Jeremy (1982), „From the history of a simple group”, The Mathematical Intelligencer, 4 (2): 59–67, doi:10.1007/BF03023483, MR 0672918 . Reprinted in Levy, Silvio, ed. (1999), The Eightfold Way, MSRI Publications, 35, Cambridge University Press, pp. 115–131, ISBN 0-521-66066-1, MR 1722415 
• en Manivel, L. (2006), „Configurations of lines and models of Lie algebras”, Journal of Algebra, 304 (1): 457–486, arXiv:math/0507118 , doi:10.1016/j.jalgebra.2006.04.029 
• en Plücker, J. (1839), Theorie der algebraischen Curven: gegrundet auf eine neue Behandlungsweise der analytischen Geometrie, Berlin: Adolph Marcus 
• en Riemann, G. F. B. (1876), „Zur Theorie der Abel'schen Funktionen für den Fall p = 3”, Ges. Werke, Leipzig, pp. 456–472 . As cited by Cayley.
• en Shioda, Tetsuji (1995), „Weierstrass transformations and cubic surfaces” (PDF), Commentarii Mathematici Universitatis Sancti Pauli, 44 (1): 109–128, MR 1336422 
• en Trott, Michael (1997), „Applying GroebnerBasis to Three Problems in Geometry”, Mathematica in Education and Research, 6 (1): 15–28