Reologie
Reologia este știința ce studiază interdependența între solicitările mecanice, răspunsul corpurilor și proprietățile acestora. Această știință stabilește modelele matematice care descriu comportamentul corpurilor supuse la solicitări. Acest comportament este determinat de dependența dintre forțe (solicitări) și răspuns (deformare, de exemplu).
O forță sau un sistem de forțe aplicat unui corp conduce la mișcarea acestuia. Mișcarea corpului poate consta în deplasări (translație sau/și rotație) sau/și deformări (modificarea formei sau/și volumului). În general, deplasarea nu modifică poziția relativă a elementelor ce formează corpul, dar modifică poziția acestuia, în raport cu un sistem de referință exterior. Deformarea determină modificarea poziției relative a elementelor constituente.
Deformarea, în cazul solidelor, are loc până la atingerea echilibrului între forțele interne și externe. Gradul de deformare se schimbă continuu în timp pentru fluide care nu ajung la o deformație de echilibru. Curgerea este fenomenul în care deformația crește continuu și nu se mai recuperează după îndepărtarea forței. Curgerea are un rol important în majoritatea operațiilor specifice tehnologiilor de sinteză și prelucrare a polimerilor.
Concepte de bază ale reologiei[modificare | modificare sursă]
Tensiunea (efortul unitar)[modificare | modificare sursă]
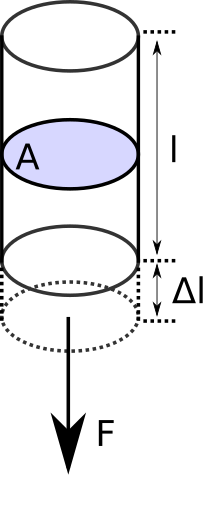
Tensiunea este forța care acționează pe suprafața unui corp, când suprafața tinde la zero. Tensiunile se pot clasifica în funcție de direcția aplicării forței pe suprafața corpului în:
- tensiunea normală, care se notează cu (forța este aplicată perpendicular pe o față a corpului și va produce o deformare care va modifica volumul și va lăsa forma neschimbată)
- tensiunea tangențială, care se notează cu (forța este aplicată tangențial sau paralel pe o față a corpului și va produce modificarea formei corpului și menținerea neschimbată a volumului)
Tensiunea se calculează cu următoarea formulă:
unde
- = tensiunea normală;
- F = forța aplicată;
- A = suprafața corpului care susține forța.

Deformația[modificare | modificare sursă]
Sub acțiunea unei tensiuni un corp se deformează. Deformația poate modifica volumul sau forma corpului. De asemenea, deformația poate fi elastică și se recuperează la descărcarea corpului, sau poate fi curgere și rămâne nerecuperată.
Deformația specifică sau relativă este raportul dintre variația în lungime produsă datorită solicitării și lungimea inițială a segmentului de dreaptă. Trebuie să facem distincția între deformația specifică (care se notează cu ) produsă de tensiuni normale și lunecarea specifică (care se notează cu ) produsă de tensiuni tangențiale.
Deformația specifică se calculează cu următoarea formulă:
unde
- = deformația specifică;
- l = variația în lungime;
- l = lungimea inițială.
Există diferite tipuri de deformații:
- compresia - tensiunile normale sunt orientate spre interiorul corpului și volumul se micșorează
- dilatarea - tensiuni normale sunt orientate spre exteriorul corpului și volumul se mărește
- forfecare simplă
- forfecare pură
- rotație
Compresia și dilatarea fac parte din categoria deformațiilor volumice.
Constante elastice[modificare | modificare sursă]
Rezistența la solicitările transversale se exprimă prin modulul de elasticitate transversal, G, iar rezistența la solicitările normale se exprimă prin modulul de elasticitate longitudinal, E. Se calculează astfel:
unde
- E = modulul de elasticitate longitudinal;
- = tensiunea normală;
- = deformația specifică;
și
unde
- G = modulul de elasticitate transversal;
- = tensiunea tangențială;
- = lunecarea specifică.
Viteza de deformare (gradientul vitezei)[modificare | modificare sursă]
Sub acțiunea unor solicitări externe corpurile deformabile se pot deforma cu viteze diferite. Deformarea poate fi instantanee sau are loc într-un interval finit de timp. Viteza de deformare sau gradientul vitezei este viteza cu care diverse planuri (într-un corp) sau molecule (într-un lichid) se mișcă unele relativ la celălalte.
Viscoelasticitate[modificare | modificare sursă]
Măsuratori reologice[modificare | modificare sursă]
Reometria este tehnica de măsurare a mărimilor care caracterizează un material cu proprietăți reologice.[1] Reometrul este un instrument pentru studierea și măsurarea caracteristicilor reologice ale materialelor.[2] Reometrele pot măsura mărimi cum ar fi viscozitatea, coeficienții tensiunilor normale sau diferite module dinamice. În mod ideal, un reometru ar trebui să fie capabil să detecteze modificările proprietăților reologice ale sistemului în condiții similare de solicitare cu cele din realitate.[3]
Există multe tipuri de reometre[4]:
- Viscozimetre cu bulă și cupe viscozimetrice
- Viscozimetre cu bilă sau cu cilindru
- Viscozimetre capilare
- Reometre rotaționale
- Reometre cu cilindri concentrici
- Reometre con-placă și reometre cu plăci paralele
- Reometre cu geometrii speciale
- Reometre dinamice
- Reometre cu tensiune controlată
- Reometre pentru curgere extensională
Pentru caracterizarea comportării reologice a materialelor plastice, există două tipuri de experiențe[5]:
- experiențe de fluaj, în care se înregistrează creșterea deformației sub tensiune constantă și din care se deduce complianța fluajului;
- teste de relaxare a tensiunii, în care se măsoară scăderea tensiunii în condițiile unei deformații constante și din care se poate obține modulul de relaxare a tensiunilor.
Aplicații[modificare | modificare sursă]
Reologia este deosebit de importantă în industria alimentară, industria farmaceutică și cosmetică și în industria petrolieră și chimică.
Multe produse cosmetice sunt suspensii sau emulsii pentru care reologia este deosebit de importantă. De exemplu, componentele solide ale amestecului trebuie să fie distribuite uniform în produs sau readuse în suspensie cu ușurință prin agitare. Caracteristicile reologice ale amestecului vor determina tendința componentelor solide de a se sedimenta la partea inferioară a recipientului. În cazul rujurilor, reologia va influența transferul uniform al produsului pe buze, precum și menținerea formei și a consistenței la temperaturi mai ridicate. În cazul unui răsturnări, conținutul nu trebuie să picure din recipient în timpul aplicării, ci trebuie să fie transferat cu ușurință pe piele. Odată aplicat, produsul nu trebuie să curgă sub acțiunea forței gravitaționale, ci trebuie să rămână pe piele.[6]
Pentru cosmetice, nu numai controlul curgerii este important, ci și asigurarea absenței curgerii atunci când este necesar. Astfel, o pastă de dinți trebuie să-și recupereze structura și viscozitatea inițială după de este depusă pe periuță, iar o cremă sau un șampon trebuie să aibă o consistență suficientă pentru a nu curge cu ușurință din mână înainte de a fi aplicată. Chiar și faza de spumă a șamponului trebuie să fie stabilă pe păr și să nu curgă cu ușurință iritând ochii utilizatorului.[7]
În industria vopselelor, caracteristicile reologice vor determina aplicabilitatea vopselei, gradul de șiroire și de uniformitate a dispersiei, prevenind sau controlând sedimentarea pigmenților.[8]
În industria de polimeri, metoda de preparare a amestecurilor polimerice controlează morfologia amestecului care, la rândul ei determină proprietățile reologice ale amestecului. Pe de altă parte, proprietățile reologice determină alegerea condițiilor de prelucrare (temperatură, grad de forfecare etc.), care, la rândul lor, au o influență determinantă asupra proprietăților fizico-mecanice ale produsului finit.[9]
Vezi și[modificare | modificare sursă]
Note[modificare | modificare sursă]
- ^ „Definiție reometrie, DEX online”. Accesat în .
- ^ „Definiție reometru, DEX online”. Accesat în .
- ^ C. Ibanescu Reologia sistemelor polimerice multifazice page 122
- ^ C. Ibanescu Reologia sistemelor polimerice multifazice page 123-131
- ^ C. Ibanescu Reologia sistemelor polimerice multifazice page 90
- ^ C. Ibanescu Reologia sistemelor polimerice multifazice page 47
- ^ C. Ibanescu Reologia sistemelor polimerice multifazice page 38-39
- ^ C. Ibanescu Reologia sistemelor polimerice multifazice page 58
- ^ C. Ibanescu Reologia sistemelor polimerice multifazice page 82
Bibliografie[modificare | modificare sursă]
- en J. Heller, Biomaterials Science. An Introduction to Materials in Medicine, Properties of Materials (capitol), Academic Press, 1996.
- C. Ibanescu, Reologia sistemelor polimerice multifazice, Introducere (capitol), [1] Arhivat în , la Wayback Machine.









