Graf orientat

În matematică, și mai precis în teoria grafurilor, un graf orientat (sau digraf) este un graf ale cărui muchii au asociat un sens.
Definiție
[modificare | modificare sursă]Din punct de vedere formal, un graf orientat este o pereche ordonată G = (V, A) unde[1]
- V este o mulțime ale cărei elemente se numesc noduri sau vârfuri;
- A este o mulțime de perechi ordonate de noduri, numite săgeți, muchii orientate (uneori, pur și simplu muchii cu mulțimea corespunzătoare notată cu E în loc de A), arce, sau linii orientate.
Aceasta diferă de un graf neorientat sau obișnuit, prin aceea că acesta din urmă este definit în termeni de perechi neordonate(d) de noduri, numite de regulă muchii sau linii.
Definiția de mai sus nu permite unui graf orientat să aibă mai multe arce cu aceleași noduri sursă și destinație, dar unii autori consideră o definiție mai largă, care permit grafurilor orientate să aibă mai multe arce (și anume, ele permit mulțimii de arce să fie o multimulțime). Mai precis, aceste entități sunt abordate ca multigrafuri orientate (sau multidigrafuri). Pe de altă parte, definiția de mai sus permite unui graf orientat să aibă bucle (adică săgeți care leagă nodurile de ele însele), dar unii autori consideră o definiție mai restrânsă, care nu permite grafurilor orientate să aibă bucle.[2] Mai precis, grafurile orientate fără bucle sunt abordate ca grafuri orientate simple, în timp ce grafurile orientate cu bucle sunt abordate ca digrafuri cu bucle (a se vedea secțiunea Tipuri de grafuri orientate).
Tipuri de grafuri orientate
[modificare | modificare sursă]Subclase
[modificare | modificare sursă]
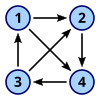
- Grafuri orientate simetrice sunt grafuri orientate în care toate muchiile sunt bidirecționate (adică pentru fiecare arc care aparține digrafului, arcul corespunzător inversat aparține și el digrafului).
- Grafuri orientate simple sunt grafuri orientate care nu au bucle (arce care leagă nodurile cu ele însele) și nu există mai multe arce cu aceleași noduri sursă și destinație. În cazul în care sunt mai multe astfel de arce, ele sunt de obicei denumite multigrafuri orientate. Unii autori numesc digrafurile cu bucle digrafuri-buclă.
- Grafuri orientate complete sunt grafurile orientate în care fiecare pereche de noduri este însoțită de o pereche simetrică de arce (este echivalent cu un graf complet neorientat cu muchiile înlocuite de perechi de arce). Rezultă că un digraf complet este simetric.
- Grafurile turneu sunt grafuri orientate obținute prin alegerea unei direcții pentru fiecare muchie într-un graf neorientat complet.
- Grafurile aciclice orientate sunt grafuri orientate fără cicluri orientate.
- Multiarborii sunt arbori aciclici orientați în care nu există două drumuri orientate dintr-un nod de pornire care să ducă în același nod final.
- Arborii orientați sau poliarborii sunt grafuri orientate aciclice formate prin orientarea muchiilor unui graf aciclic neorientat.
- arborii cu rădăcină sunt arbori orientați în care toate muchiile arborelui neorientat asociat sunt îndreptate în sensul opus rădăcinii.
Terminologia de bază
[modificare | modificare sursă]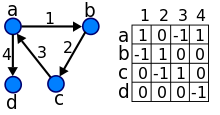
Un arc (x, y) este considerat a fi îndreptată de la x la y; y se numește capul și x se numește coada; se spune că y este un succesor direct al lui x și x este numit predecesor direct al lui y. Dacă un drum duce de la x la y, atunci y este declarat a fi un succesor al lui x și accesibil din x, iar x este declarat a fi un predecesor al lui y. Arcul (y, x) se numește arcul inversat al lui (x, y).
Matricea de adiacență a unui multidigraf cu bucle este matricea de întregi, ale cărei linii și coloane corespund nodurilor, unde un element nediagonal aij este numărul de arce din nodul i la nodul j, iar elementul diagonal aii este numărul de bucle ale nodului i. Matricea de adiacență a unui graf orientat este invariantă la permutarea de linii și coloane.
O altă matrice de reprezentare pentru un graf orientat este matricea de incidență(d).
Grad interior și grad exterior
[modificare | modificare sursă]
Pentru un nod, numărul de capete adiacente unui nod este numit gradul interior al nodului și numărul de cozi adiacente unui nod este gradul exterior (numit și „factor de ramificare” la arbori).
Fie G = (V, A) și v∈V. Gradul interior al lui v este notată cu deg−(v) și gradul exterior este notat cu deg+(v).
Un nod cu deg−(v) = 0 se numește sursă, întrucât este originea tuturor arcelor care ies. În mod similar, un nod cu deg+(v) = 0 se numește drenă, deoarece este direcția în care sunt îndreptate toate arcele adiacente.
Dacă un nod nu este nici sursă, nici drenă, este numit intern.
Formula sumei gradelor afirmă că, pentru un graf orientat,
Dacă pentru fiecare nod v∈V, deg+(v) = deg−(v), graful este numit un graf orientat echilibrat.[3]
Șirul gradelor
[modificare | modificare sursă]Șirul gradelor unui graf orientat este lista perechilor formate din gradul interior și gradul exterior asociat nodului; pentru exemplul de mai sus, avem șirul gradelor ((2, 0), (2, 2), (0, 2), (1, 1)). Șirul gradelor este invariant al unui graf orientat, deci grafurile orientate izomorfe au același șir al gradelor. Cu toate acestea, șirul gradelor nu identifică, în general, în mod unic un graf orientat; în unele cazuri, digrafuri neizomorfe au același șir de grade.
Problema realizării unui graf orientat(d) este problema de a găsi un graf orientat cu un șir de grade dat. (Perechile de zerouri pot fi ignorate, deoarece acestea sunt ușor de realizat prin adăugarea unui număr adecvat de noduri izolate în graf.) Un șir care este șir de grade al unui graf orientat, adică pentru care realizarea grafului orientat are o soluție, este numit un grafic orientat sau șir grafic orientat. Această problemă poate fi rezolvată prin algoritmul Kleitman–Wang(d) sau prin teorema Fulkerson–Chen–Anstee(d).
Conectivitatea unui graf orientat
[modificare | modificare sursă]Un graf orientat este slab conex (sau doar conex[4]) dacă graful de bază neorientat obținut prin înlocuirea tuturor arcelor din graful orientat cu muchii neorientate este un graf conex. Un graf orientat este tare conex dacă conține un drum orientat de la x la y și un drum orientat de la y la x pentru orice pereche de noduri {x, y}. Componentele tare conexe sunt subgrafuri tare conexe maximale.
Note
[modificare | modificare sursă]- ^ Bang-Jensen & Gutin (2000).
- ^ Chartrand, Gary (). Introductory Graph Theory. Courier Corporation. ISBN 9780486247755.
- ^ Satyanarayana, Bhavanari; Prasad, Kuncham Syam, Discrete Mathematics and Graph Theory, PHI Learning Pvt. Ltd., p. 460, ISBN 978-81-203-3842-5
- ^ Bang-Jensen & Gutin (2000) p. 19 in the 2007 edition; p. 20 in the 2nd edition (2009).
Bibliografie
[modificare | modificare sursă]- en Bang-Jensen, Jørgen; Gutin, Gregory (), directed graphs: Theory, Algorithms and Applications, Springer, ISBN 1-85233-268-9 Mai multe valori specificate pentru
|ISBN=și|isbn=(ajutor)
(editia 1 corectată din 2007, este acum disponibil gratuit pe site-ul autorilor; a 2-a ediție a apărut în 2009 ISBN: 1-84800-997-61-84800-997-6). - en Bondy, John Adrian; Murty, U. S. R. (), Graph Theory with Applications, North-Holland, ISBN 0-444-19451-7, arhivat din original la , accesat în Mai multe valori specificate pentru
|ISBN=și|isbn=(ajutor). - en Diestel, Reinhard (), Graph Theory (ed. 3rd), Springer, ISBN 3-540-26182-6 Mai multe valori specificate pentru
|ISBN=și|isbn=(ajutor) (ediția a 3-a electronică este disponibilă gratuit pe site-ul autorului). - en Harary, Frank; Norman, Robert Z.; Cartwright, Dorwin (), Structural Models: An Introduction to the Theory of Directed Graphs, New York: Wiley.
- Numărul de grafuri orientate (sau grafuri orientate) cu n noduri din Enciclopedia on-line a șirurilor întregi

