CUSUM

În controlul statistic al proceselor, CUSUM (sau diagrama de sumă cumulativă) este o tehnică de analiză secvențială dezvoltată de E.S. Page de la Universitatea din Cambridge. Aceasta este de obicei folosită pentru monitorizarea și detectarea schimbărilor.^[1] CUSUM a fost publicată în jurnalul Biometrika^⁠(d), în 1954, la câțiva ani după publicarea algoritmului SPRT^⁠(d) de către Wald.^[2]

Page menționa un „număr de calitate” $\theta$ $\theta$ $\theta$ , care reprezenta un parametru al distribuției de probabilitate, de exemplu, media. El a conceput CUSUM ca o metodă de determinare a modificărilor din punctul de vedere al acestui număr $\theta$ și a propus un criteriu pentru a decide când sunt necesare măsuri corective. Atunci când metoda CUSUM este aplicată modificărilor mediei, poate fi utilizată pentru detectarea salturilor într-o serie temporală.

Câțiva ani mai târziu, George Alfred Barnard^⁠(d) a dezvoltat o metodă de vizualizare, diagrama măștilor în V, pentru a detecta atât creșteri, cât și scăderi în $\theta$ .^[3]

Metodă[modificare | modificare sursă]

După cum sugerează și numele, CUSUM presupune cumularea sumei (ceea ce o face „secvențială”). Observațiilor dintr-un proces $x_{n}$ le sunt atribuite ponderi $\omega _{n}$ și sunt însumate după cum urmează:

S_{0}=0

S_{n+1}=\max(0,S_{n}+x_{n}-\omega _{n})

Atunci când valoarea S depășește o anumită valoare de prag, se consideră că a fost identificată o schimbare. Formula de mai sus detectează doar modificări în direcție pozitivă. Când trebuie identificate schimbări negative, în loc de operațiunea max trebuie să fie folosită operațiunea min, iar de această dată o schimbare este identificată atunci când valoarea S este sub valoarea (posibil negativă) de prag.

Page nu a menționat în mod explicit că $\omega$ reprezintă funcția de probabilitate, dar aceasta este interpretarea utilizată.

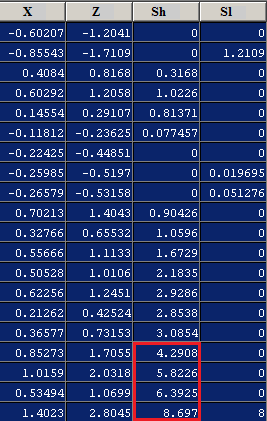
Exemplu[modificare | modificare sursă]

Următorul exemplu ilustrează 20 de observații dintr-un proces cu o valoare medie a X egală cu 0 și o deviație standard de 0,5. Se poate observa că valoarea lui Z nu este mai mare decât 3, deci alte diagrame de control nu ar trebui să fi detectat o schimbare, în timp ce folosind Cusum 17 arată valoarea de SH este mai mare decât 4.

Coloană	Descriere
$X$	Observațiile procesului cu media ${\bar {x}}$ =0 și deviație standard $\sigma _{X}$ =0.5
$Z$	Obervațiile normalizate, adică centrate în jurul mediei și scalate cu deviația standard $Z_{n}={\frac {X_{n}-{\bar {x}}}{\sigma _{X}}}$
$S_{H}$	Valoarea CUSUM pozitivă, care detectează o anomalie pozitivă, ${S_{H}}_{n+1}=\max(0,{S_{H}}_{n}+Z_{n}-\omega )$
$S_{L}$	Valoarea CUSUM negativă, care detectează o anomalie negativă, ${S_{L}}_{n+1}=\max(0,{S_{L}}_{n}-Z_{n}-\omega )$

Note[modificare | modificare sursă]

^ Grigg; Farewell, VT; Spiegelhalter, DJ; et al. (2003). „The Use of Risk-Adjusted CUSUM and RSPRT Charts for Monitoring in Medical Contexts”. Statistical Methods in Medical Research. 12 (2): 147–170. doi:10.1177/096228020301200205. PMID 12665208.
^ Page, E. S. (iunie 1954). „Continuous Inspection Scheme”. Biometrika. 41 (1/2): 100–115. doi:10.1093/biomet/41.1-2.100. hdl:10338.dmlcz/135207 . JSTOR 2333009.
^ Barnard, G.A. (1959). „Control charts and stochastic processes”. Journal of the Royal Statistical Society^⁠(d). B (Methodological) (21, number 2): 239–71. JSTOR 2983801.

[grigg-1] Grigg; Farewell, VT; Spiegelhalter, DJ; et al. (2003). „The Use of Risk-Adjusted CUSUM and RSPRT Charts for Monitoring in Medical Contexts”. Statistical Methods in Medical Research. 12 (2): 147–170. doi:10.1177/096228020301200205. PMID 12665208.

[page-2] Page, E. S. (iunie 1954). „Continuous Inspection Scheme”. Biometrika. 41 (1/2): 100–115. doi:10.1093/biomet/41.1-2.100. hdl:10338.dmlcz/135207 . JSTOR 2333009.

[3] Barnard, G.A. (1959). „Control charts and stochastic processes”. Journal of the Royal Statistical Society^⁠(d). B (Methodological) (21, number 2): 239–71. JSTOR 2983801.

[1]

[2]

[3]