Distanță Hamming
 |
 |
 | |
|---|---|
 | |
În teoria informației, distanța Hamming dintre două șiruri de lungime egală este numărul de poziții ale căror simboluri corespunzătoare sunt diferite. Cu alte cuvinte, ea măsoară numărul minim de substituții necesare pentru a schimba un șir în celălalt, sau numărul minim de erori care au transformat un șir în celălalt.
Exemple[modificare | modificare sursă]
Distanța Hamming dintre:
- 1011101 și 1001001 este 2.
- 2173896 și 2233796 este 3.
- "pacte" și "carte" este 2.
Proprietăți speciale[modificare | modificare sursă]
Pentru o lungime fixată n, distanța Hamming este o metrică în spațiul vectorial al cuvintelor de această lungime, deoarece în mod evident îndeplinește condițiile de ne-negativitate, reflexivitate și simetrie, și poate fi demonstrat ușor prin inducție completă că satisface și inegalitatea triunghiulară. Distanța Hamming dintre două cuvinte a și b poate fi văzută și ca ponderea Hamming pentru a−b, la o alegere potrivită a operatorului −.
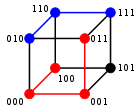
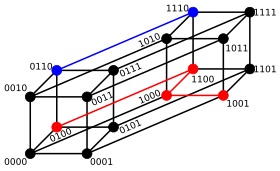
Pentru șirurile binare a și b, distanța Hamming este egală cu numărul de biți 1 din a xor b. Spațiul metric al șirurilor binare de lungime n, împreună cu distanța Hamming, este cunoscut drept cubul Hamming. Un șir binar de lungime n poate fi văzut și ca un vector în considerând fiecare simbol ca o coordonată reală; în aceste condiții, șirurile formează vârfurile unui hipercub n-dimensional, iar distanța Hamming a șirurilor este echivalentă distanței Manhattan dintre vârfuri.

