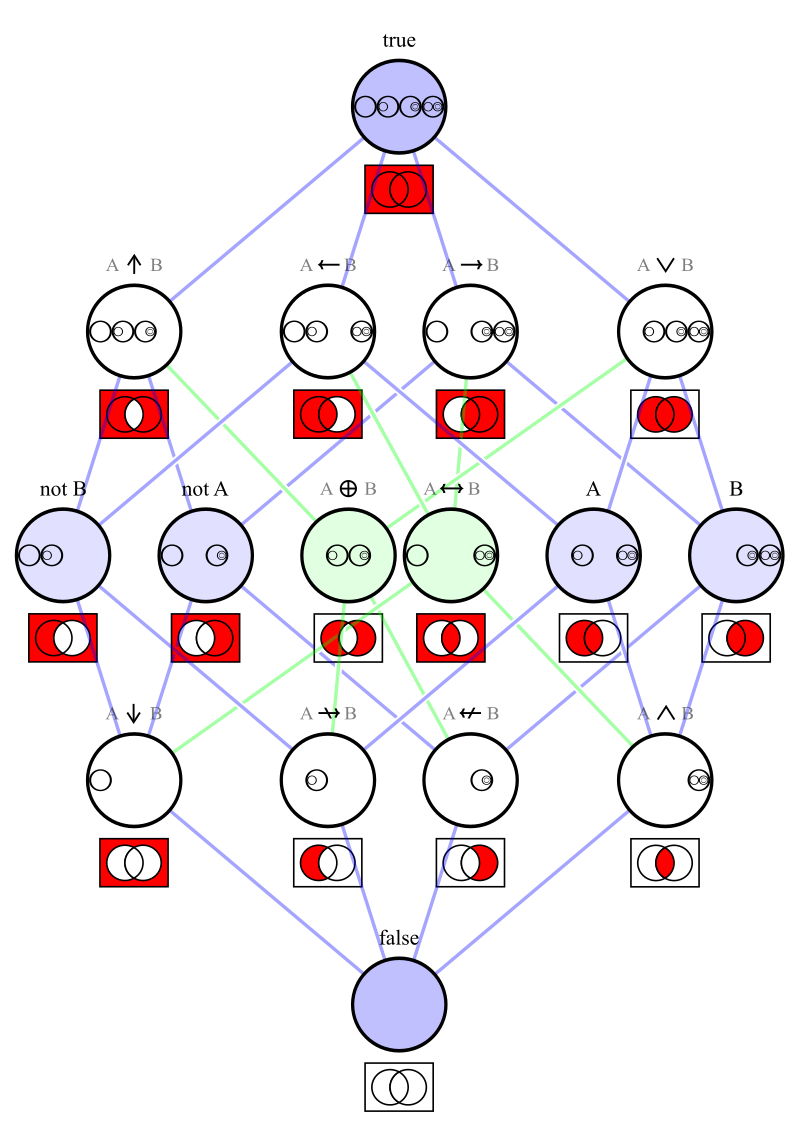
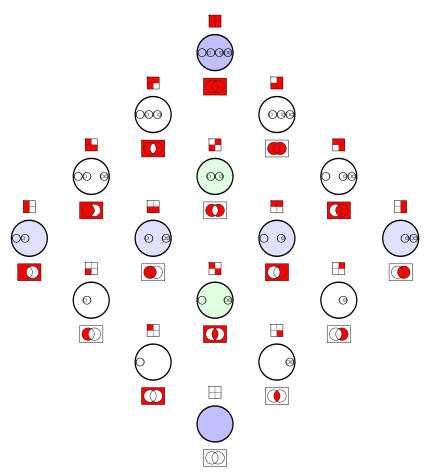
Fișier:Venn0001.svg
Aspect

Mărimea acestei previzualizări PNG a acestui fișier SVG: 400 × 300 pixeli. Alte rezoluții: 320 × 240 pixeli | 640 × 480 pixeli | 1.024 × 768 pixeli | 1.280 × 960 pixeli | 2.560 × 1.920 pixeli.
Mărește rezoluția imaginii (Fișier SVG, cu dimensiunea nominală de 400 × 300 pixeli, mărime fișier: 613 octeți)
Istoricul fișierului
Apăsați pe Data și ora pentru a vedea versiunea trimisă atunci.
| Data și ora | Miniatură | Dimensiuni | Utilizator | Comentariu | |
|---|---|---|---|---|---|
| actuală | 16 iulie 2024 18:10 |  | 400x300 (613 octeți) | Antonsusi | validizing, easier code |
| 2 martie 2024 02:14 |  | 384x280 (3 KB) | Watchduck | cleaner code and lighter red (overwritten with Pywikibot) | |
| 26 iulie 2009 17:06 |  | 384x280 (3 KB) | Watchduck | ||
| 26 iulie 2009 17:05 |  | 384x280 (3 KB) | Watchduck | ||
| 26 ianuarie 2008 16:24 |  | 615x463 (4 KB) | Watchduck | {{Information |Description= |Source=eigene arbeit |Date= |Author= Tilman Piesk |Permission= |other_versions= }} | |
| 22 ianuarie 2008 18:57 |  | 615x463 (4 KB) | Watchduck | {{Information |Description=Venn diagrams (sometimes called Johnston diagrams) concerning propositional calculus and set theory |Source=own work |Date=2008/Jan/22 |Author=Tilman Piesk |Permission=publich domain |other_versions= }} | |
| 22 ianuarie 2008 17:26 |  | 480x360 (3 KB) | Watchduck | {{Information |Description= |Source= |Date= |Author= |Permission= |other_versions= }} |
Utilizarea fișierului
Următoarele pagini conțin această imagine:
Utilizarea globală a fișierului
Următoarele alte proiecte wiki folosesc acest fișier:
- Utilizare la als.wikipedia.org
- Utilizare la am.wikipedia.org
- Utilizare la anp.wikipedia.org
- Utilizare la ar.wikipedia.org
- Utilizare la ast.wikipedia.org
- Utilizare la az.wikipedia.org
- Utilizare la ba.wikipedia.org
- Utilizare la be-tarask.wikipedia.org
- Utilizare la be.wikipedia.org
- Utilizare la bg.wikipedia.org
- Utilizare la bn.wikipedia.org
- Utilizare la ca.wikipedia.org
- Utilizare la ckb.wikipedia.org
- کۆمەڵە (ماتماتیک)
- ژێرکۆمەڵ
- ئەندام (بیرکاری)
- کۆمەڵەی بەتاڵ
- گیۆرگ کانتۆر
- کۆمەڵەی بێکۆتایی
- کۆمەڵەی بەکۆتایی
- دەروازە:ماتماتیک
- فانکشن (ماتماتیک)
- داڕێژە:تووڵی دەروازە
- مۆدیوول:Portal/images/ت
- داڕێژە:تووڵی دەروازە/doc
- دەروازە:ماتماتیک/دەروازە پەیوەندیدارەکان
- پۆل:تیۆریی کۆمەڵە
- بواری بەرامبەر
- دەروازە:ئەندازە
- دەروازە:ئەندازە/دەروازە پەیوەندیدارەکان
- دەروازە:جەبر
- دەروازە:جەبر/دەروازە پەیوەندیدارەکان
- دەروازە:ئامار
- دەروازە:ئامار/دەروازە پەیوەندیدارەکان
- دەروازە:شیکاریی ماتماتیکی
- دەروازە:شیکاریی ماتماتیکی/دەروازە پەیوەندیدارەکان
Vizualizați utilizările globale ale acestui fișier.