Tensiune superficială

Tensiunea superficială este proprietatea generală a lichidelor de a lua o formă geometrică de arie minimă în lipsa forțelor externe, datorată acțiunii forțelor de coeziune dintre moleculele lichidului. Această proprietate face ca porțiunea de suprafață a lichidului să fie atrasă de altă suprafață, cum ar fi cea a unei alte suprafețe de lichid, ca în cazul fuzionării picăturilor de apă sau a formării de sfere din picăturile de mercur.
Aplicând fizica newtoniană forțelor ce apar din cauza tensiunii superficiale se obțin predicții precise pentru numeroase comportamente ale lichidelor, comportamente atât de comune încât sunt în general luate ca atare. Aplicând termodinamica acelorași forțe, rezultă predicții pentru alte comportamente mai subtile ale lichidelor.
Mărimea fizică ce caracterizează tensiunea superficială este coeficientul de tensiune superficială, notată de regulă cu litera grecească σ (sigma), uneori cu γ (gamma), care este o mărime fizică intensivă, caracteristică fiecărei substanțe omogene în condiții fizice date (constantă de material)
Coeficientul de tensiune superficială are dimensiune de forță pe unitatea de lungime, sau de energie pe unitatea de arie. Cele două sunt echivalente — dar când se face referire la energie pe unitatea de arie, se preferă termenul de energie superficială — termen mai general, în sensul că se aplică și solidelor, nu doar lichidelor.
Cauze[modificare | modificare sursă]


Tensiunea superficială se datorează atracției dintre moleculele lichidului prin intermediul forțelor intermoleculare. În interiorul masei lichidului, fiecare moleculă este atrasă în egală măsură în toate direcțiile de către moleculele învecinate, în condiții de echilibru termodinamic, din care cauză rezultanta tuturor forțelor este nulă, în raport cu centrul de masă al moleculei considerate. La suprafața lichidului, moleculele sunt atrase înspre interior de alte molecule aflate în adâncimea lichidului și mai puțin de moleculele din mediul învecinat (fie el vid, aer sau un alt lichid).[1] Astfel, toate moleculele de la suprafață sunt supuse unei forțe rezultante de atracție moleculară îndreptate spre interior, echilibrată în celălalt sens doar de rezistența la compresie a lichidului, ceea ce înseamnă o forță rezultantă nulă. Există, însă, o forță ce determină diminuarea suprafeței libere a lichidului, și în acest sens, suprafața unui lichid se aseamănă cu o membrană elastică. Din cauza aceasta, sub acțiunea forțelor moleculare din partea masei de lichid, suprafața liberă a lichidului tinde să ia forma ce corespunde celei mai mici suprafețe locale.[1]
Din alt punct de vedere, se constată că o moleculă în contact cu o altă moleculă vecină este într-o stare de energie mai mică decât dacă nu ar fi în contact cu acea a doua moleculă. Moleculele interioare au toate numărul maxim de vecini pe care îl pot avea. Dar moleculele de la margine au mai puțini vecini decât cele interioare și deci sunt într-o stare de energie mai mare. Pentru ca lichidul să-și minimizeze starea energetică, el trebuie să minimizeze numărul de molecule de la margine și deci să-și minimizeze aria suprafeței.[2][3]
Ca rezultat al minimizării ariei, suprafața unui lichid va prelua forma cea mai uniformă pe care o poate avea (demonstrația matematică a faptului că formele „uniforme” minimizează aria suprafeței se bazează pe ecuația Euler–Lagrange). Cum orice curbură a formei suprafeței duce la mărirea ariei, va rezulta și o energie mai mare. În consecință, suprafața va împinge înapoi înspre orice curbură în același fel în care o minge împinsă la deal va împinge înapoi pentru a-și minimiza energia potențială gravitațională.
Efecte vizibile în viața de zi cu zi[modificare | modificare sursă]


Efectele tensiunii superficiale pot fi văzute în cazul apei:
- Formarea de picături de apă pe suprafața caroseriei ceruite a unui automobil. Apa are aderență slabă cu ceara și puternică cu ea însăși, și astfel apa se adună în picături. Tensiunea superficială le dă o formă cvasisferică, fiindcă sfera are cel mai mic raport între aria suprafeței și volum
- Formarea de picături are loc atunci când o masă de lichid este întinsă. Animația arată apa care aderă la gura robinetului și care câștigă în masă până când greutatea ei crește dincolo de punctul în care tensiunea superficială nu o mai poate ține legată de robinet. După aceea, ea se separă și tensiunea superficială formează picătura sferică. Dacă din robinet ar fi curs un flux continuu de apă, acesta s-ar fi dezmembrat în picături pe parcursul căderii. Gravitația întinde fluxul de apă, după care tensiunea superficială îl strânge în sfere.[4]
- Plutirea de obiecte mai dense ca apa are loc când obiectul nu se umezește și greutatea sa este suficient de mică pentru a fi contrabalansată de forțele ce rezultă din tensiunea superficială.[3]
- Separarea uleiului de apă este cauzată de o diferență între tensiunile superficiale ale lichidelor diferite.
- Lacrimile de vin reprezintă formarea de picături și curgeri pe marginea unui pahar ce conține o băutură alcoolică. Cauzele sale se regăsesc în interacțiunile complexe dintre tensiunile superficiale diferite între apă și etanol.
Tensiunea superficială apare și în alte fenomene comune, mai ales când se folosesc unele substanțe care o reduc:
- Baloanele de săpun au suprafețe foarte mari cu volum foarte mic. Baloanele de apă pură sunt instabile. Adăugarea de surfactanți, însă, poate avea efect stabilizator asupra baloanelor (efectul Marangoni). Surfactanții reduc tensiunea superficială a apei de cel puțin trei ori.
- Emulsiile sunt un tip de soluție în care joacă un rol și tensiunea superficială. Mici fragmente de ulei suspendate în apă pură se adună spontan în mase mult mai mari. Dar prezența unui surfactant duce la scăderea tensiunii superficiale, care permite stabilitatea micilor picături de ulei în masa apei (sau viceversa).
Bazele fizice[modificare | modificare sursă]
Două definiții[modificare | modificare sursă]

Dintre toate corpurile geometrice, forma sferică posedă, la un volum determinat, cea mai mică arie. Din acest motiv, schimbarea formei nesferice ale unei mase determinate de lichid într-o formă sferică, atrage după sine micșorarea ariei suprafeței de delimitare a lichidului de mediul înconjurător. Prin urmare, efectul forțelor presiunii moleculare, sub influența cărora lichidul ia forma sferică, este analoagă acțiunii care ar apărea dacă suprafața lichidului ar reprezenta o membrană elastică ce tinde să se contracte (strângă)[5] Fenomenele fizice determinate de existența presiunii moleculare se pot explica prin aplicarea modelului unei astfel de membrane superficiale care delimitează volumul lichidului studiat, de mediul său înconjurător.[1][6]
Pentru menținerea unei membrane întinsă în echilibru static, la marginea ei trebuie să existe o forță F, tangentă la suprafața lichidului și normală la marginea suprafeței; forța aceasta se numește forță de tensiune superficială. Acestă forță este direct proporțională cu lungimea l a marginii membranei de lichid; pentru a scrie expresia matematică a forței de tensiune superficială se introduce un coeficient de proporționalitate, numit coeficientul de tensiune superficială, reprezentat prin simbolul σ și care depinde de natura lichidului.[6] Dependența forței de tensiune superficială de lungime se exprimă prin formula: . Coeficientul tensiunii superficiale este definit ca fiind forța pe unitatea de lungime, unde forța este paralelă cu suprafața, dar perpendiculară pe direcția lungimii.[1] Din expresia forței de tensiune se poate scrie formula de definiție a coeficientului de tensiune superficială:[5]
|
.
Cu alte cuvinte, coeficientul este numeric egal cu forța aplicată pe unitatea de lungime a marginii suprafeței membranei de lichid.[1][5][6][7]
Un mod intuitiv de a înțelege dependența forței de lungime este exemplul dat de o peliculă plană de săpun delimitată de o buclă de ață întinsă, de lungime l. Ața va fi trasă spre interiorul peliculei (membranei) de o forță egală cu 2L (factorul numeric 2 apare din cauză că pelicula de săpun are două fețe, și deci două suprafețe, astfel încât ața se „racordează” de două ori la membrană).[8] Tensiunea superficială are deci dimensiune de forță pe unitate de lungime.[6] În Sistemul Internațional unitatea sa este newtonul pe metru, dar în cgs unitatea sa este dina pe cm.[6][9] O dină/cm corespunde la 0,001 N/m.
O definiție echivalentă pentru coeficientul de tensiune superficială, utilă în termodinamică, este lucrul mecanic efectuat pe unitatea de suprafață.[6] Astfel, pentru a crește aria suprafeței libere a unei mase de lichid cu o cantitate, ΔA, este necesară o cantitate de lucru mecanic ΔA.[8] Acest lucru mecanic se transformă în energie potențială. Cum sistemele mecanice izolate încearcă să găsească o stare de energie potențială minimă, potrivit principiului minimei acțiuni, o picătură liberă de lichid preia în mod natural o formă sferică, formă de suprafață minimă pentru un volum dat.[5]

Pentru deducerea relației corecte dintre energia membranei, variația ariei și coeficientul de tensiune superficială se consideră o membrană de lichid dreptunghiulară întinsă pe un cadru rigid de înălțime l, având una din înălțimi (o latură) mobilă și de masă neglijabilă (vezi figura din dreapta). În vederea determinării lucrului mecanic necesar pentru a mări aria membranei superficiale de lichid cu o cantitate ΔA, se deplasează prin translație latura mobilă a membranei pe o distanță ΔS sub acțiunea unei forțe externe F.[5][10] Procesul de întindere a membranei este unul cvasistatic, de aceea, această forță este permanent în echilibru cu rezultanta forțelor de tensiune superficială care se opun deplasării spre dreapta. În aceste condiții, lucrul mecanic efectuat de către forța F împotriva forțelor de tensiune superficială este .[10] Conform relației de definiție a forței de tensiune superficială ; din aceste două relații rezultă expresia lucrului mecanic corespunzător creșterii ariei membranei:
Produsul este egală cu variația ΔA a ariei membranei astfel încât:[10]
Lucrul mecanic efectuat asupra membranei contribuie la creșterea energiei potențiale a membranei, adică , de unde
Relație din care se scrie o a doua definiție pentru coeficientul de tensiune superficială:
|
.
Energia potențială E este fracțiunea din energia internă a membranei care pe parcursul unei transformări izoterme poate fi transformat în lucru mecanic. În termodinamică această parte a energiei se numește energie liberă (generalizat: potențialul Gibbs).[10] Ultima relație dă definiția fizică a coeficientului , și anume: coeficientul de tensiune superficială este numeric egal cu variația energiei libere a membranei superficiale raportat la variația ariei acestei membrane.[10]
Formulă dimensională și unități de măsură[modificare | modificare sursă]
Conform analizei dimensionale, formula dimensională pentru după prima definiție se scrie sub forma:
Adică dimensiunea fizică a coeficientului de tensiune superficială este masa ori timpul la puterea minus doi.
În Sistemul Internațional de Măsuri forța se măsoară în N iar lungimea în m, rezultă că unitatea de măsură pentru coeficientul tensiunii superficiale în SI este:
Adică: unitatea de măsură a tensiunii superficiale în SI este newton pe metru sau newton ori metru la puterea minus unu. În sistemul cgs ea se măsoară în dyn pe centimetru sau dyn ori centimetru la puterea minus unu.
După a doua definiție, unitatea de măsură este:
În consecință tensiunea superficială poate fi măsurată în SI și ca jouli pe metru pătrat și în cgs ca ergi pe cm2.[6][10]
Echivalența energiei pe unitate de suprafață cu forța pe unitatea de lungime se poate demonstra prin analiză dimensională.[6][8] Prin egalarea celor două expresii ale coeficientului de tensiune superficială rezultă relațiile:
Exemple sugestive pentru efectele tensiunii superficiale[modificare | modificare sursă]
Acțiunea peliculei de lichid asupra unui fir[modificare | modificare sursă]

În imaginea animată din dreapta este prezentat un experiment simplu care demonstrează acțiunea tensiunii superficiale asupra membranelor de lichid. O peliculă subțire de soluție apoasă de săpun este întinsă pe „buza” unui pahar, între două puncte diametral opuse ale marginii paharului se află legat un fir textil ușor care are o formă oarecare. Inițial, forma firului este stabilă datorită faptului că forțele de tensiune superficială care acționează de o parte și alta sunt în echilibru. În momentul în care experimentatorul „sparge” pelicula din partea de jos, forțele de tensiune superficială acționează unilateral numai din partea de sus, reducând aria peliculei rămase la minimum iar firul textil este întins, luând o formă curbă corespunzătoare ariei minime. Configurația finală, de „semilună”, a ansamblului peliculă-fir corespunde celei mai coborâte valori a energiei potențiale.
Insecte pe suprafața liberă a apei[modificare | modificare sursă]

Cele două insecte care se împerechează utilizează tensiunea superficială pentru a sta pe suprafața apei. Suprafața liberă a apei se comportă ca o membrană elastică: picioarele insectelor, în contact cu suprafața apei, determină îndoirea acesteia, crescându-i aria. Aceasta reprezintă o creștere a energiei potențiale datorită tensiunii superficiale care apare în regiunea deformată a apei egală cu scăderea de energie potențială rezultată din coborârea centrului de masă al insectelor; prin aceasta se realizează un echilibru energetic în sensul că variația energiei ansamblului insecte-peliculă de apă este nulă. Fenomenul se poate explica și din punct de vedere static, prin echilibrarea forței de greutate ale celor două insecte de rezultanta forțelor de tensiune superficială ce acționează din partea peliculei de apă deformată asupra picioarelor insectelor[11]
Propulsia datorită tensiunii superficiale interfaciale[modificare | modificare sursă]

Curbura suprafeței și presiunea[modificare | modificare sursă]

Dacă nu acționează nicio forță normală asupra suprafeței aflată sub acțiunea tensiunii, ea trebuie să rămână plană. Dar dacă presiunea de o parte a suprafeței diferă de cea de partea cealaltă, diferența de presiune înmulțită cu aria are ca rezultantă o forță normală. Pentru ca forțele de tensiune superficiale să anuleze forța normală dată de presiune, suprafața trebuie să fie curbată. Diagrama arată cum curbura unui element de suprafață duce la o componentă netă a forțelor de tensiune, normală pe centrul elementului de suprafață. Starea de echilibru care se realizează este descrisă de ecuația ecuația Young–Laplace:[2][6]
unde:
- este diferența de presiune.
- este tensiunea superficială.
- și sunt razele de curbură după fiecare axă paralelă cu suprafața.
Cantitatea din paranteza din partea dreaptă a ecuației este de fapt dublul curburii medii a suprafeței (în funcție de normalizare).
Soluțiile acestei ecuații determină forma picăturilor de apă, petelor, meniscurilor, baloanelor de săpun și ale tuturor celorlalte forme determinate de acțiunea tensiunii superficiale (cum ar fi forma urmelor insectelor pe suprafața apei).
Tabelul de mai jos arată cum crește presiunea internă a picăturii de apă cu scăderea razei. Pentru picături nu foarte mici efectul este neglijabil, dar diferența de presiune devine enormă atunci când picăturile ajung la dimensiuni moleculare.
| Δp pentru picături de apă de raze diferite în condiții standard de presiune și temperatură | ||||
|---|---|---|---|---|
| Raza picăturii | 1 mm | 0,1 mm | 1 μm | 10 nm |
| Δp (atm) | 0,0014 | 0,0144 | 1,436 | 143,6 |
Suprafața de arie minimă a unei pelicule cu delimitare arbitrară[modificare | modificare sursă]

Pentru a găsi forma suprafeței minimale pentru pelicula limitată de un cadru cu o geometrie arbitrară folosind doar mijloace matematice, se impune rezolvarea unui sistem de ecuații diferențiale cuplate, supuse condițiilor la frontieră, care este un calcul dificil. Realizând respectivul cadru din sârmă și scufundându-l într-o soluție de săpun, între tronsoanele cadrului se va forma o peliculă de suprafață aproximativ minimală (cea exactă doar în imponderabilitate) în câteva secunde. Fără a efectua niciun calcul, pelicula ajunge singură la soluția unei minimizări complexe.[8][12]
Motivul pentru aceasta este acela că diferența de presiune de-a lungul unei interfețe fluide este proporțională cu curbura medie, după cum arată ecuația Young-Laplace. Pentru o peliculă de săpun deschisă, diferența de presiune este zero, și deci curbura medie este și ea zero, iar suprafețele minimale au ca proprietate nulitatea curburii medii.
Fenomene de contact între lichide și solide[modificare | modificare sursă]
Unghiuri de racordare și tensiunea interfacială[modificare | modificare sursă]
Cum niciun lichid nu poate exista într-un vid perfect perioade lungi de timp din cauza evaporării rapide, suprafața oricărui lichid este o interfață între acel lichid și un alt mediu. Suprafața unui lac, de exemplu, este o interfață între apa din lac și aer. Atunci, tensiunea superficială nu este doar o proprietate a lichidului, ci o proprietate a interfeței lichidului cu un alt mediu. Dacă un lichid este într-un recipient, atunci în afara interfeței lichid/aer la suprafața de sus, există și o interfață între lichid și pereții recipientului. Tensiunea superficială între lichid și aer este de regulă mai mare decât tensiunea superficială de la contactul cu pereții recipientului. Și acolo unde se întâlnesc două suprafețe, geometria lor trebuie să fie în așa fel ca toate forțele să fie în echilibru.[2][6][8]
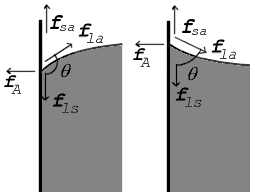 |
Când cele două suprafețe se întâlnesc, ele formează un unghi de racordare, , care este unghiul pe care tangenta la suprafață îl face cu suprafața solidă. Diagrama din dreapta prezintă două exemple. Forțele de tensiune sunt prezentate pentru interfața lichid-aer, interfața lichid-solid și interfața solid-aer. În exemplul din stânga, diferența dintre tensiunile superficiale lichid-solid și solid-aer, , este mai mică decât tensiunea superficială lichid-aer, , dar totuși pozitivă, și anume
În diagramă, atât forțele verticale cât și cele orizontale trebuie să se anuleze exact în punctul de contact. Componenta orizontală a lui este anulată de forța de adeziune, .[8]
Componenta verticală a lui trebuie să anuleze exact forța .[8]
| Lichid | Solid | Unghiul de racordare | |||
|---|---|---|---|---|---|
| apă |
|
0° | |||
| etanol | |||||
| dietil eter | |||||
| tetraclorură de carbon | |||||
| glicerol | |||||
| acid acetic | |||||
| apă | ceară de petrol | 107° | |||
| argint | 90° | ||||
| iodură de metil | sticlă obișnuită | 29° | |||
| cristal de plumb | 30° | ||||
| cuarț obișnuit | 33° | ||||
| mercur | sticlă obișnuită | 140° | |||
| Câteva unghiuri de contact lichid-solid[8] | |||||
Întrucât forțele sunt direct proporționale cu tensiunile superficiale respective, avem și:[2][6]
unde
Aceasta înseamnă că deși diferența dintre tensiunile superficiale lichid-solid și solid-aer, , este dificil de măsurat direct, ea poate fi calculată cu ușurință pe baza unghiului de racordare, , dacă se cunoaște tensiunea superficială lichid-aer, .[6]
Aceeași relație există și în diagrama din dreapta. Dar în acest caz se vede că deoarece unghiul de racordare este mai mic de 90°, diferența de tensiune superficială lichid-solid/solid-aer trebuie să fie negativă:
Unghiuri de racordare particulare[modificare | modificare sursă]
În cazul particular al unghiului de racordare al unei interfețe apă-argint la care unghiul de racordare este egal cu 90°, diferența de tensiune superficială lichid-solid/solid-aer este exact zero.
Un alt caz particular îl reprezintă unghiul de racordare de exact 180°. Apa împreună cu un teflon special pregătit se apropie de această valoare.[2] Unghiul de racordare de 180° se realizează când tensiunea superficială lichid-solid este exact egală cu tensiunea superficială lichid-aer.[6]
Metode de măsurare[modificare | modificare sursă]

Întrucât tensiunea superficială are numeroase efecte, există mai multe căi de a o măsura. Metoda optimă depinde de natura lichidului măsurat, de condițiile în care se măsoară tensiunea și de stabilitatea suprafeței la deformare.
- Metoda inelului du Noüy: Metoda tradițională utilizată pentru măsurarea tensiunii superficiale sau interfaciale. Proprietățile suprafeței legate de umezire au o influență restrânsă asupra acestei tehnici. Se măsoară forța maximă exercitată de suprafață asupra inelului.[13]
- O versiune minimizată a metodei Du Noüy utilizează un ac metalic cu diametru mic în loc de inel, în combinație cu o microbalanță de mare sensibilitate pentru măsurarea forței maxime. Avantajul acestei metode este acela că se pot măsura volume foarte mici (până la ordinul zecilor de microlitri) cu foarte mare precizie, fără a trebui să se efectueze corecții pentru flotabilitate (pentru un ac cu geometria corectă). În plus, măsurarea se poate efectua foarte rapid, în minim 20 de secunde.
- Metoda plăcilor Wilhelmy: O metodă universală potrivită pentru măsurarea tensiunii superficiale pe intervale de timp lungi. O placă verticală de perimetru cunoscut se atașează la o balanță, și se mășoară forța datorată umezirii.[14]
- Metoda rotației picăturii: Această tehnică este ideală pentru măsurarea tensiunilor interfaciale mici. Se măsoară diametrul unei picături într-o fază grea în timp ce ambele se rotesc.
- Metoda picăturii: Prin această tehnică se pot măsura tensiunea superficială și cea interfacială, chiar la temperaturi și presiuni ridicate. Geometria unei picături se analizează optic.[14]
- Metoda lui Jaeger: O tehnică de măsurare pentru determinarea tensiunii superficiale la durate de rezistență mici ale suprafețelor. Se măsoară presiunea minimă pe fiecare balon.
- Metoda volumului picăturii: O metodă pentru determinarea tensiunii interfaciale ca funcție de vârsta interfeței. Un lichid cu o densitate este pompat într-un al doilea lichid cu o densitate diferită și se măsoară timpul între formarea picăturilor.[15]
- Metoda creșterii în tub capilar: Capătul unui tub capilar este scufundat într-o soluție. Înălțimea până la care urcă soluția în interiorul tubului capilar este legată de tensiunea superficială prin ecuația discutată mai jos.[16]
- Metoda stalagmometrică: O metodă ce constă în cântărirea șî analizarea unei picături de lichid.
- Metoda picăturii legate: O metodă de determinare a tensiunii superficiale și a densității prin plasarea unei picături pe un substrat și măsurarea unghiului de contact.[17]
- Metoda cu cerneală de test: O metodă de măsurare a tensiunii superficiale a substratelor folosind cerneală de test și interpretând reacția cernelii. Vezi video.
Efecte[modificare | modificare sursă]
Lichid într-un tub vertical[modificare | modificare sursă]

Un barometru cu mercur constă dintr-un tub vertical de sticlă de aproximativ 1 cm diametru umplut parțial cu mercur, și cu vid (denumit vid Toricelli) în volumul neumplut (vezi diagrama din dreapta). Nivelul mercurului din centrul tubului este mai înalt decât la margini, suprafața superioară a mercurului fiind în formă de dom. Centrul de masă al întregii coloane de mercur ar fi puțin mai jos dacă mercurul ar fi plat de-a lungul secțiunii transversale a tubului, dar forma de dom dă o arie a suprafeței puțin mai mică întregii mase de mercur. Din nou, cele două efecte se combină pentru a minimiza energia potențială totală. O astfel de formă a suprafeței se numește menisc convex.
Motivul pentru care se consideră aria suprafeței întregii mase de mercur, inclusiv porțiunea care se află în contact cu sticla, este că mercurul nu aderă deloc la sticlă. Astfel, tensiunea superficială a mercurului acționează asupra suprafeței sale totale, inclusiv a celei aflate în contact cu sticla. Dacă în loc de sticlă tubul ar fi fost din cupru, situația ar fi fost foarte diferită. Mercurul aderă cu agresivitate la cupru. Deci într-un tub de cupru, nivelul mercurului în centrul tubului va fi mai mic decât pe margini (ar prezenta menisc concav). Într-o situație în care lichidul aderă la pereții recipientului, se consideră că partea suprafeței fluidului care se află în contact cu recipientul are tensiune superficială negativă. Fluidul atunci încearcă să maximizeze aria suprafeței de contact. Deci în acest caz creșterea ariei de contact cu recipientul reduce energia potențială în loc să o mărească. Această scădere este suficientă pentru a compensa creșterea de energie potențială asociată cu ridicarea fluidului în apropierea pereților recipientului.

Dacă un tub este suficient de îngust și adeziunea lichidului la pereții săi este suficient de mare, tensiunea superficială poate trage lichidul în sus pe tub, într-un fenomen denumit capilaritate. Înălțimea coloanei ridicate este dată de relația:[8]
unde
- este înălțimea lichidului ridicat,
- este coeficientul de tensiune superficială lichid-aer,
- este densitatea lichidului,
- este raza tubului capilar,
- este accelerația gravitațională,
- este unghiul de racordare descris mai sus. Dacă este mai mare de 90°, cum este cazul mercurului într-un recipient de sticlă, lichidul va coborî în tub, în loc să urce.
Pete pe o suprafață[modificare | modificare sursă]


Turnarea de mercur pe un geam orizontal plat are ca efect formarea unei pete de grosime vizibilă. (Nu încercați decât în condiții de asigurare a protecției antitoxice. Vaporii de mercur sunt extrem de toxici!) Pata se va împrăștia doar până în punctul în care are o grosime de puțin sub un centimetru. Și aceasta se datorează acțiunii tensiunii superficiale puternice a mercurului. Masa lichidului se aplatizează deoarece astfel mare parte din mercur este adusă la un nivel energetic cât de jos posibil. Dar tensiunea superficială, în același timp, acționează spre a reduce suprafața totală. Rezultă o stare de echilibru: o pată cu o grosime aproape fixă.
Aceeași demonstrație se poate face și cu apa, dar numai pe o suprafață la care apa nu aderă, ca de exemplu ceara. Apa turnată pe o suprafață ceruită, netedă și curată se va comporta similar mercurului turnat pe geam.
Grosimea petei de lichid pe o suprafață al cărui unghi de contact este de 180° este dată de:[2]
unde
este adâncimea petei în centimetri sau metri. este tensiunea superficială a lichidului în dyn pe centimetru sau în newtoni pe metru. este accelerația gravitațională egală cu 980 cm/s2 sau 9,8 m/s2 este densitatea lichidului în grame pe centimetru cub sau în kilograme pe metru cub

În realitate, grosimea petelor va fi puțin mai mică decât cea prezisă de formula de mai sus, deoarece foarte puține suprafețe au unghi de racordare de 180° cu vreun lichid. Când unghiul de racordare este mai mic de 180°, grosimea este dată de expresia:[2]
Pentru mercur pe sticlă, , și , și deci . Pentru apă pe parafină la 25 °C, , și ceea ce dă .
Formula prezice și că atunci când unghiul de racordare este aproape de 0°, lichidul se va împrăștia într-un strat foarte subțire pe toată suprafața. O astfel de suprafață se numește perfect umectabilă de lichid.
Dezintegrarea jeturilor în picături[modificare | modificare sursă]

În viața de zi cu zi, se poate observa că un jet de apă ce iese dintr-un robinet se dezintegrează în picături, indiferent cât de lin curgea el inițial. Aceasta se datorează unui fenomen denumit instabilitatea Plateau–Rayleigh,[2][6] care este, în întregime, o consecință a efectelor tensiunii superficiale.
Explicația acestei instabilități începe cu existența unor mici perturbații în jet. Acestea sunt prezente întotdeauna, indiferent cât de laminară este curgerea lichidului. Dacă perturbațiile sunt dezvoltate în componente sinusoidale, se observă că unele componente se amplifică în timp, în timp ce altele se atenuează în timp. Dintre cele care se amplifică, unele cresc mai rapid ca altele. Dacă o componentă se atenuează sau se amplifică, și cât de rapid crește ea depinde de numărul său de undă (o măsură a numărului de maxime și minime pe centimetru) și de raza jetului cilindric inițial.[6]
Termodinamică[modificare | modificare sursă]
După cum s-a arătat mai sus, lucrul mecanic elementar necesar creșterii unei suprafețe cu un element de arie este . Deci la temperatură și presiune constantă, coeficientul de tensiune superficială este egală cu energia liberă Gibbs pe aria suprafeței:[2]
unde este energia liberă Gibbs și este aria.
Legile termodinamicii impun ca orice schimbare spontană de stare să fie însoțită de o scădere a energiei libere Gibbs.
De aici rezultă motivul pentru care scăderea ariei suprafeței unei mase de lichid este întotdeauna spontană (), dacă nu este însoțită de alte schimbări energetice. Deci, pentru a crește aria suprafeței, trebuie să se adauge o anumită cantitate de energie.
Energia liberă Gibbs este definită de ecuația[18] , unde este entalpia și este entropia. De aici și din faptul că tensiunea superficială este energia liberă Gibbs pe aria suprafeței, se poate obține următoarea expresie pentru entropia pe unitatea de arie:
Ecuația lui Kelvin pentru suprafețe rezultă din rearanjarea ecuației de mai sus. Ea afirmă că entalpia suprafeței sau energia suprafeței depind ambele de coeficientul de tensiune superficială și de derivata ei în raport cu temperatura la presiune constantă prin relația:[19]
Termodinamica balonului de săpun[modificare | modificare sursă]
Presiunea din interiorul unui balon de săpun ideal (cu o singură suprafață) poate fi calculată din considerațiile termodinamice privind energia liberă. La temperatură și număr de particule constante, , energia liberă Helmholtz fiind dată de:
unde este diferența de presiune în interiorul și în exteriorul balonului, iar este tensiunea superficială. La echilibru, , și deci,
- .
Pentru un balon sferic, volumul și aria suprafeței sunt date de relațiile
- ,
și
- .
Înlocuind aceste relații în expresia anterioară, rezultă
- ,
care este echivalent cu ecuația Young-Laplace când Rx = Ry. Pentru baloane de săpun reale, presiunea se dublează din cauza prezenței a două interfețe, una interioară și alta exterioară.
Influența temperaturii[modificare | modificare sursă]


Coeficientul de tensiune superficială depinde de temperatură.[6] Din acest motiv, când se exprimă o anume valoare a tensiunii superficiale a unei suprafețe de contact, trebuie specificată explicit și temperatura. Tendința generală este ca tensiunea superficială să scadă cu creșterea temperaturii, ajungând la o valoare de 0 la temperatura critică.[6] Există doar unele ecuații empirice care fac legătura între tensiunea superficială și temperatură:
Aici V este volumul molar al substanței, TC este temperatura critică și k este o constantă valabilă pentru aproape toate substanțele.[13] O valoare tipică este k = 2.1 x 10−7. [J K−1 mol-2/3] [13][20] Pentru apă, se poate folosi și V = 18 ml/mol și TC = 374 °C.
O variantă a ecuației Eötvös este descrisă de Ramsay și Shields:[18]
unde diferența de temperatură de 6 kelvini face formula să corespundă mai bine realității la temperaturi joase.
- Guggenheim-Katayama:[19]
este o constantă a fiecărui lichid și n este un factor empiric, a cărui valoare este 11/9 pentru lichidele organice. Această ecuație a fost propusă și de van der Waals, care a propus și ca să fie dat de expresia , unde este o constantă universală a tuturor lichidelor, iar este Presiunea critică a lichidului (deși experimentele ulterioare au relevat că variază puțin de la un lichid la altul).[19]
Atât Guggenheim-Katayama cât și Eötvös țin cont de faptul că valoarea coeficientului de tensiune superficială atinge 0 la temperatura critică, pe când teoria lui Ramsay și Shields nu e valabilă la acest punct extrem.
Influența compoziției soluțiilor[modificare | modificare sursă]
Solvații pot avea efecte asupra tensiunii superficiale în funcție de structura lor:
- Efect redus sau inexistent, cum e cazul zahărului
- Creștere a tensiunii superficiale, ca la sărurile anorganice
- Scăderea progresivă a tensiunii superficiale, ca la alcooli
- Scăderea tensiunii superficiale până la un punct dincolo de care nu mai au niciun efect, cum este cazul surfactanților
Ceea ce complică acest efect este faptul că un solvat poate exista în concentrații diferite la suprafață și în masa soluției. Această diferență variază de la un amestec solvat/solvent la altul.
Izoterma Gibbs afirmă că:[18]
- se numește concentrația superficială, și reprezintă excesul de solvat pe unitatea de arie a suprafeței supra cât solvat ar fi prezent dacă concentrația s-ar păstra aceeași ca și în masa soluției. Unitatea de măsură este mol/m2
- este concentrația substanței din masa soluției.
- este constanta gazelor și este temperatura
Izoterma Gibbs se bazează pe unele ipoteze simplificatoare, deci ea poate fi aplicată doar în soluții ideale (foarte diluate) cu doi compuși.
Influența dimensiunii particulelor asupra presiunii vaporilor[modificare | modificare sursă]
Ecuația Clausius-Clapeyron conduce la o altă ecuație atribuită și ea lui Kelvin și care explică de ce, din cauza tensiunii superficiale, presiunea vaporilor pentru picături mici de lichid în suspensie este mai mare decât presiunea standard a vaporilor aceluiași lichid când suprafața de contact este plană, adică atunci când un lichid formează picături mici, concentrația de echilibru a vaporilor săi în mediu este mai mare. Aceasta se întâmplă fiindcă presiunea din interiorul picăturii este mai mare decât cea din afara ei.[18]

- este presiunea standard a vaporilor pentru lichidul respectiv la presiunea și temperatura respective.
- este volumul molar.
- este constanta gazelor
este raza Kelvin, raza picăturilor.
Efectul explică suprasaturația vaporilor. În absența punctelor de nucleație, trebuie să se formeze mici picături înainte ca ele să evolueze în picături mai mari. Aceasta necesită o presiune a vaporilor de multe ori mai mare decât presiunea vaporilor în punctul tranziției de fază.[18]
Această ecuație este folosită și în chimia catalizatorilor pentru a evalua mezoporozitatea solidelor.[21]
Acest efect poate fi văzut în termeni de număr mediu de vecini moleculari ai moleculelor de la suprafață (vezi diagramă).
Tabelul următor prezintă câteva valori calculate pentru acest efect în cazul apei la diferite dimensiuni ale picăturilor:
| P/P0 pentru picături de apă la diferite raze în condiții normale de presiune și temperatură[19] | ||||
|---|---|---|---|---|
| Raza picăturii (nm) | 1000 | 100 | 10 | 1 |
| P/P0 | 1.001 | 1.011 | 1.114 | 2.95 |
Efectul devine mai clar pentru picături de dimensiune foarte mică, întrucât pe o rază de 1 nm se află aproximativ 100 de molecule, cantitate suficient de mică pentru a impune o analiză cuantică.
Tabel de date[modificare | modificare sursă]
| Lichid | Temperatură °C | Tensiunea superficială, γ |
|---|---|---|
| Acid acetic | 20 | 27.6 |
| Acid acetic (40.1%) + apă | 30 | 40.68 |
| Acid acetic (10.0%) + apă | 30 | 54.56 |
| Acetonă | 20 | 23.7 |
| Dietil eter | 20 | 17.0 |
| Etanol | 20 | 22.27 |
| Etanol (40%) + apă | 25 | 29.63 |
| Etanol (11,1%) + apă | 25 | 46.03 |
| Glicerol | 20 | 63 |
| n-Hexan | 20 | 18.4 |
| Acid clorhidric 17.7M soluție apoasă | 20 | 65.95 |
| Izopropanol | 20 | 21.7 |
| Mercur | 15 | 487 |
| Metanol | 20 | 22.6 |
| n-Octan | 20 | 21.8 |
| Clorură de sodiu 6.0M soluție apoasă | 20 | 82.55 |
| Zaharoză (55%) + apă | 20 | 76.45 |
| Apă | 0 | 75.64 |
| Apă | 25 | 71.97 |
| Apă | 50 | 67.91 |
| Apă | 100 | 58.85 |
Galerie de efecte[modificare | modificare sursă]
-
Despărţirea unei pelicule de apă în mişcare la ricoşarea dintr-o lingură.
-
Fotografie a apei în curgere aderând la o mână. Tensiunea superficială creează pelicula de apă dintre mână şi curgere.
-
Un balon de săpun echilibrează forţele de tensiune cu presiunea pneumatică internă.
-
Tensiunea superficială împiedică scufundarea unei monede: moneda este în mod cert mai densă ca apa, deci nu poate pluti doar din cauza flotabilităţii.
-
O margaretă. Întreaga floare se află sub nivelul suprafeţei libere. Apa creşte uniform în jurul marginilor. Tensiunea superficială împiedică apa să scufunde floarea.
-
Fotografie ce prezintă fenomenul „lacrimi de vin”, indus de o combinaţie a modificării tensiunii superficiale a apei cu etanol împreună cu faptul că etanolul se evaporă mai rapid ca apa.
-
O agrafă de metal pluteşte pe apă. Se mai pot adăuga şi altele fără ca apa să se reverse.
-
O monedă de aluminiu pluteşte pe o suprafaţă a apei la 10 °C. Orice greutate suplimentară ar duce la scufundarea monedei.
Vezi și[modificare | modificare sursă]
Bibliografie[modificare | modificare sursă]
în limba română[modificare | modificare sursă]
- M.-I. Sălăjan, A. Mocanu, M. Tomoaia-Cotișel, Progrese în termodinamica, hidrodinamica și biofizica straturilor subțiri, Presa Universitară Clujeană, 2004
- Dima, Ion și alții: Dicționar de fizică, Editura enciclopedică română, București, 1980, (pag.46-47, 448-449)
- Florea, J. și Panaitescu, V.: Mecanica Fluidelor, Editura didactică și pedagogică, București, 1986, capitolul I: Statica fluidelor, (pag.34-45)
- Friș, S.E. și Timoreva, A.V. : Curs de Fizică Generală, vol. I. (traducere din limba rusă) Editura Tehnică, București, 1964, capitolul IX: Fenomene moleculare în lichide (pag.389-407)
- Iacob, Caius și alții: Dicționar de mecanică, Editura științifică și enciclopedică, București, 1980, (pag.59,285,461-462)
- Murgulescu, I.G și Segal, E.: Introducere în chimia fizică, vol.II.1, Teoria molecular cinetică a materiei, Editura Academiei RSR, București, 1979, secțiunea a V-a: Starea Lichidă, capitolul XXVIII: Proprietăți de echilibru, (pag.723-739)
în limbi străine[modificare | modificare sursă]
- ^ a b c d e Friș și Timoreva, op. cit, pag. 389
- ^ a b c d e f g h i j Pierre-Gilles de Gennes; Françoise Brochard-Wyart; David Quéré (). Capillary and Wetting Phenomena — Drops, Bubbles, Pearls, Waves. Tradus de Alex Reisinger. Springer. ISBN 0-387-00592-7.
- ^ a b c White, Harvey E. (). Modern College Physics. van Nostrand. ISBN 0442294018.
- ^ John W. M. Bush (). „MIT Lecture Notes on Surface Tension, lecture 5” (PDF). Massachusetts Institute of Technology. Accesat în . Parametru necunoscut
|dateformat=ignorat (ajutor) - ^ a b c d e Dima și alții, op. cit. pag. 449
- ^ a b c d e f g h i j k l m n o p q r Florea și Panaitescu, op. cit. pag. 34-35
- ^ Murgulescu p 728-729
- ^ a b c d e f g h i j Sears, Francis Weston; Zemanski, Mark W. University Physics 2nd ed. Addison Wesley 1955
- ^ John W. M. Bush (2004). „MIT Lecture Notes on Surface Tension, lecture 1” (PDF). Massachusetts Institute of Technology. Accesat în April 1 2007. Parametru necunoscut
|dateformat=ignorat (ajutor); Verificați datele pentru:|access-date=(ajutor) - ^ a b c d e f Friș și Timoreva, op. cit., pag. 390
- ^ John W. M. Bush (). „MIT Lecture Notes on Surface Tension, lecture 3” (PDF). Massachusetts Institute of Technology. Accesat în . Parametru necunoscut
|dateformat=ignorat (ajutor) - ^ Aaronson, Scott. „SIGACT News”.
|contribution=ignorat (ajutor) - ^ a b c d „Surface Tension by the Ring Method (Du Nouy Method)” (pdf). PHYWE. Accesat în .
- ^ a b „Surface and Interfacial Tension”. Langmuir-Blodgett Instruments. Accesat în .
- ^ „Surfactants at interfaces” (PDF). lauda.de. Arhivat din original (PDF) la . Accesat în .
- ^ Calvert, James B. „Surface Tension (physics lecture notes)”. University of Denver. Accesat în .
- ^ „Sessile Drop Method”. Dataphysics. Arhivat din original la . Accesat în .
- ^ a b c d e Moore, Walter J. (). Physical Chemistry, 3rd ed. Prentice Hall.
- ^ a b c d e Adam, Neil Kensington (). The Physics and Chemistry of Surfaces, 3rd ed. Oxford University Press.
- ^ a b „Physical Properties Sources Index: Eötvös Constant”. Arhivat din original la . Accesat în .
- ^ G. Ertl, H. Knözinger and J. Weitkamp; Handbook of heterogeneous catalysis, Vol. 2, page 430; Wiley-VCH; Weinheim; 1997
- ^ Lange's Handbook of Chemistry, 10th ed. pp 1661–1665
Legături externe[modificare | modificare sursă]
 Materiale media legate de Tensiune superficială la Wikimedia Commons
Materiale media legate de Tensiune superficială la Wikimedia Commons- ebooks.unibuc.ro: Determinarea tensiunii superficiale a unui lichid prin metoda presiunii maxime in bula si variatia ei cu temperatura
- ebooks.unibuc.ro: Determinarea tensiunii superficiale a unui lichid prin metoda stalagmometrică
- Generalități, pe scurt, despre tensiunea superficială
- Despre tensiunea superficială și cazuri practice interesante
- Note de curs despre tensiunea superficială de la MIT Arhivat în , la Wayback Machine.
- Teoria măsurării tensiunii superficiale
- Tensiunea superficială a diferitelor lichide
- Calculul tensiunii superficiale în funcție de temperatură pentru unii compuși comuni
- The Bubble Wall[nefuncțională] (slideshow audio de la National High Magnetic Field Laboratory în care se explică coeziunea, tensiunea superficială și legăturile de hidrogen)











![{\displaystyle [\sigma ]={\frac {[F]}{[l]}}=M\cdot T^{-2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a99faa3e4447549bcb9a4b9371084cdbb0ffe64d)
![{\displaystyle [\sigma ]_{SI}={\frac {[F]_{SI}}{[l]_{SI}}}={\frac {N}{m}}=N\cdot m^{-1}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/64cb5d061c190fe962a507aa3b2ce0a9bc0b5426)
![{\displaystyle [\sigma ]_{SI}={\frac {[E]_{SI}}{[A]_{SI}}}={\frac {J}{m^{2}}}=J\cdot m^{-2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4685ecc4150b35cb1aeee82625051dc63e64e5e5)
























































































