Polinoame Hermite
| Deși acest articol conține o listă de referințe bibliografice, sursele sale rămân neclare deoarece îi lipsesc notele de subsol. Puteți ajuta introducând citări mai precise ale surselor. |
În matematică, polinoamele lui Hermite reprezintă o importantă serie de funcții din clasa polinoamelor ortogonale care au fost introduse pentru prima oară în matematică în secolul al XIX-lea în cadrul studiului probabilităților, ele sunt exemple clasice de polinoame Appell așa cum sunt seriile de polinoame ale lui Bernoulli și Euler. Expresia explicită a termenilor seriei polinoamelor lui Hermite se deduce pe cale analitică prin rezolvarea ecuației diferențiale al lui Hermite. Aplicțiile directe ale polinoamelor lui Hermite se întâlnesc în domenii precum teoria probabilităților, teoria perturbaților, statistică matematică, fizică. Una din cele mai importante domenii în care utilizarea lor a condus cu succes la rezolvarea unei probleme fundamentale este mecanica cuantică unde utilizarea lor a permis găsirea funcțiilor de stare ale oscilatorului armonic cuantic și implicit a relației de cuantificare a energiei oscilatorului. Au fost denumite în onoarea matematicianului francez Charles Hermite.
Definiție[modificare | modificare sursă]
Termenul general al polinoamelor lui Hermite este definit prin una din expresiile:
, polinoamele „probabilistice” ale lui Hermite
|
sau uneori prin relația
, polinoamele „fizice” ale lui Hermite
|
Aceste două definiții nu sunt riguros echivalente, trecerea de la o formă la alta se face printr-o transformare simplă dată de formula:
Acestea sunt șirurile de polinoame Hermite de diferite varianțe. În cele ce urmează, se va urma de regulă prima convenție. Acea convenție este adesea preferată în teoria probabilităților deoarece
reprezintă densitatea de probabilitate pentru distribuția normală cu valoarea așteptată 0 și deviația standard 1.
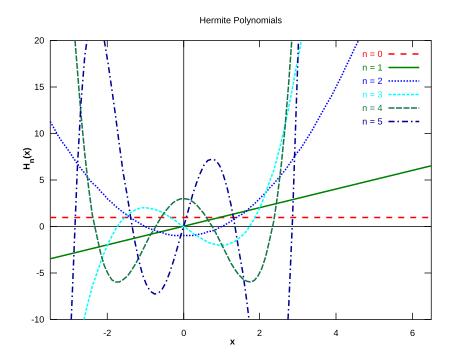
Primele unsprezece polinoame Hermite din teoria probabilităților sunt:

iar primele unsprezece polinoame Hermite din fizică sunt:
Proprietăți[modificare | modificare sursă]
Hn este un polinom de grad n. Versiunea din teoria probabilităților are coeficientul dominant 1, iar versiunea din fizică are coeficientul dominant 2n.
Ortogonalitate[modificare | modificare sursă]
Hn(x) este un polinom de gradul n pentru n = 0, 1, 2, 3, .... Aceste polinoame sunt ortogonale în raport cu funcția pondere (măsură)
- (probabilistică)
sau
- (fizică)
adică avem:
când m ≠ n. Mai mult,
- (probabilistică)
sau
- (fizică).
Polinoamele din teoria probabilităților sunt astfel ortogonale în raport cu funcția densitate de probabilitate normală standard.
Completitudine[modificare | modificare sursă]
Polinoamele Hermite (atât cele din teoria probabilităților, cât și cele din fizică) formează o bază ortogonală în spațiul Hilbert al funcțiilor care satisfac condiția
în care produsul scalar este dat de integrala ce include funcția pondere gaussiană w(x) definită în secțiunea anterioară,
O bază ortogonală pentru L2(R, w(x) dx) reprezintă un sistem ortogonal complet. Pentru un sistem ortogonal, completitudinea este echivalentă cu faptul că funcția 0 este singura funcție ƒ ∈ L2(R, w(x) dx) ortogonală pe toate celelalte funcții din sistem. Întrucât domeniul de liniaritate al polinoamelor Hermite este spațiul tuturor polinoamelor, trebuie arătat (în cazul polinoamelor din fizică) că dacă ƒ satisface condiția
pentru orice n ≥ 0, atunci ƒ = 0. O cale posibilă de a face aceasta este de a avea grijă ca funcția olomorfă
este identic nulă. Faptul că F(it) = 0 pentru orice t real înseamnă că transformata Fourier a lui ƒ(x) exp(−x2) este 0, deci ƒ este 0 în aproape toate punctele. Variante ale demonstrației de completitudine de mai sus se aplică și altor ponderi cu degradare exponențială. În cazul Hermite, este posibil și să se demonstreze o identitate explicită care implică ea însăși completitudinea (vezi secțiunea „Relații de completitudine” de mai jos).
O formulare echivalentă a faptului că polinoamele Hermite reprezintă o bază ortogonală pentru L2(R, w(x) dx) constă în introducerea funcțiilor Hermite, afirmând totodată că funcțiile Hermite reprezintă o bază ortogonală pentru L2(R).
Ecuația diferențială al lui Hermite[modificare | modificare sursă]
Polinoamele Hermite folosite în teoria probabilităților sunt soluții ale ecuației diferențiale
unde λ este o constantă, cu condițiile la limită astfel încât u să tindă polinomial la infinit. Cu aceste condiții la limită, ecuația are soluții doar dacă λ este un număr întreg pozitiv, și soluția este dată de u(x) = Hλ(x). Rescriind ecuației diferențiale sub formă de problemă de valori proprii
soluțiile sunt funcțiile proprii ale operatorului diferențial L. Această problemă de valori proprii se numește ecuație Hermite, deși termenul poate fi utilizat și pentru o altă ecuație de formă apropiată:
ale cărei soluții sunt polinoamele Hermite din fizică.
Cu niște condiții limită mai generale, polinoamele Hermite pot fi generalizate pentru a obține funcții analitice mai generale Hλ(z) pentru λ un index complex. O formulă explicită poate fi dată în termeni de integrală pe contur.[1]
Relații de recurență[modificare | modificare sursă]
Șirul polinoamelor Hermite satisface și relația de recurență
- (probabilități)
- (fizică)
Polinoamele Hermite constituie un șir Appell, deoarece satisface relația
- (probabilități)
- (fizică)
sau echivalent,
- (probabilități)
- (fizică)
Rezultă că polinoamele Hermite satisfac și relația de recurență
- (probabilități)
- (fizică)
Aceste ultime relații, împreună cu polinoamele inițiale H0(x) și H1(x), pot fi utilizate în practică pentru calculul rapid al polinoamelor.
Funcția generatoare[modificare | modificare sursă]
Polinoamele Hermite sunt date de funcția generatoare exponențială
- (probabilități)
- (fizică).
Această egalitate este valabilă pentru orice x, t complex, și se poate obține scriind dezvoltarea în serie Taylor în punctul x al funcției z → exp(−z2) (în cazul polinoamelor din fizică).
Expected value[modificare | modificare sursă]
Dacă X este o variabilă aleatoare cu distribuție normală cu deviație standard 1 și valoarea așteptată μ atunci
- (probabilități)
Relații cu alte funcții[modificare | modificare sursă]
Polinoamele Laguerre[modificare | modificare sursă]
Polinoamele Hermite pot fi exprimate sub formă de caz particular al polinoamelor Laguerre.
- (fizică)
- (fizică)
Relația cu funcția hipergeometrică confluentă[modificare | modificare sursă]
Polinoamele Hermite pot fi exprimate drept caz particular al funcțiilor cilindrului parabolic.
- (fizică)
unde este funcția hipergeometrică confluentă a lui Whittaker. Analog,
- (fizică)
- (fizică)
unde este funcția hipergeometrică confluentă a lui Kummer.
Reprezentare operatorială[modificare | modificare sursă]
Polinoamele Hermite din teoria probabilităților satisfac egalitatea
unde D reprezintă derivarea în raport cu x, iar exponențiala este interpretată prin dezvoltarea în serie de puteri. Nu există chestiuni delicate de convergență a acestei serii când operează pe polinoame, fiindcă toți termenii în afara unui număr finit dispar.
Deoarece coeficienții seriei de puteri ai exponențialei sunt cunoscuți, iar derivatele de ordin superior al monomului xn pot fi explicitate, acestă reprezentare cu operator diferențial dă naștere unei formule concrete a coeficienților lui Hn, coeficienți ce pot fi utilizați pentru calculul rapid al acestor polinoame.
Întrucât expresia formală pentru transformata Weierstrass W este eD2, se vede că transformata Weierstrass a lui (√2)nHn(x/√2) este xn. În esență, transformata Weierstrass transformă o serie de polinoame Hermite într-o serie Maclaurin corespunzătoare.
Existența unei serii de puteri formale g(D), cu coeficienți constanți și nenuli, cum ar fi Hn(x) = g(D)xn, este și ea echivalentă cu afirmația că aceste polinoame formează un șir Appell. Deoarece sunt șir Appell, ele constituie a fortiori și un șir Sheffer.
Reprezentare integrală[modificare | modificare sursă]
Polinoamele Hermite au și o reprezentare în termeni de integrală pe contur:
- (probabilități)
- (fizică)
conturul de integrare încercuind originea.
Generalizare[modificare | modificare sursă]
Polinoamele Hermite din teoria probabilităților, definite mai sus, sunt ortogonale în raport cu distribuția normală standard de probabilitate, a cărei funcție de densitate este
cu valoarea așteptată 0 și varianța 1. Se poate vorbi de polinoame Hermite
de varianță α, unde α este orice număr pozitiv. Acestea sunt ortogonale în raport cu distribuția normală de probabilitate cu funcția de densitate
Ele sunt date de
În particular, polinoamele Hermite din fizică sunt
Dacă
atunci șirul de polinoame al cărui al n-lea termen este
va fi compunerea umbrală a celor două șiruri polinomiale, și se poate arăta că satisface egalitățile:
și
Varianța negativă[modificare | modificare sursă]
Deoarece șirurile polinomiale formează un grup în raport cu operația de compunere umbrală, se poate nota că
șirul invers al celui notat similar dar fără semnul minus, și astfel se poate vorbi de polinoame Hermite de varianță negativă. Pentru α > 0, coeficienții lui Hn[−α](x) sunt doar modulele valorilor coeficienților corespunzători ai lui Hn[α](x).
Acestea apar ca momente de distribuție normală de probabilitate: Al n-lea moment al distribuției normale cu valoarea așteptată μ și varianța σ2 este
unde X este o variabilă aleatoare cu distribuția normală specificată. A special case of the cross-sequence identity then says that
Aplicații[modificare | modificare sursă]
Funcții Hermite[modificare | modificare sursă]
One can define the Hermite functions from the physicists' polynomials:
Since these functions contain the square root of the weight function, and have been scaled appropriately, they are orthonormal:
and form an orthonormal basis of L2(R). This fact is equivalent to the corresponding statement for Hermite polynomials (see above).
The Hermite functions are closely related to the Whittaker function (Whittaker and Watson, 1962) :
and thereby to other parabolic cylinder functions. The Hermite functions satisfy the differential equation:
This equation is equivalent to the Schrödinger equation for a harmonic oscillator in quantum mechanics, so these functions are the eigenfunctions.


Relații de recurență[modificare | modificare sursă]
Following recursion relations of Hermite polynomials, the Hermite functions obey
Funcțiile Hermite ca funcții proprii ale transformatei Fourier[modificare | modificare sursă]
The Hermite functions are a set of eigenfunctions of the continuous Fourier transform. To see this, take the physicist's version of the generating function and multiply by exp(−x 2/2). This gives
Choosing the unitary representation of the Fourier transform, the Fourier transform of the left hand side is given by
The Fourier transform of the right hand side is given by
Equating like powers of t in the transformed versions of the left- and right-hand sides gives
The Hermite functions are therefore an orthonormal basis of L2(R) which diagonalizes the Fourier transform operator. In this case, we chose the unitary version of the Fourier transform, so the eigenvalues are (−i) n.
Interpretarea combinatorică a coeficienților[modificare | modificare sursă]
In the Hermite polynomial Hn(x) of variance 1, the absolute value of the coefficient of xk is the number of (unordered) partitions of an n-member set into k singletons and (n − k)/2 (unordered) pairs.
Relații de completitudine[modificare | modificare sursă]
The following identity holds in the sense of distributions[necesită citare]
where δ is the Dirac delta function, (ψn) the Hermite functions, and δ(x − y) represents the Lebesgue measure on the line y = x in R2, normalized so that its projection on the horizontal axis is the usual Lebesgue measure. This distributional identity follows by letting u → 1 in the next pointwise identity, valid when −1 < u < 1
The function (x, y) → E(x, y; u) is the density for a Gaussian measure on R2 which is, when u is close to 1, very concentrated around the line y = x, and very spread out on that line. It follows that
when ƒ, g are continuous and compactly supported. This yields that ƒ can be expressed from the Hermite functions, as sum of a series of vectors in L2(R), namely
In order to prove the equality above for E(x, y; u), the Fourier transform of Gaussian functions will be used several times,
The Hermite polynomial is then represented as
With this representation for Hn(x) and Hn(y), one sees that
and this implies the desired result, using again the Fourier transform of Gaussian kernels after performing the substitution
Note[modificare | modificare sursă]
Referințe[modificare | modificare sursă]
- Format:Abramowitz Stegun ref
- B Spain, M G Smith, Functions of mathematical physics, Van Nostrand Reinhold Company, London, 1970. Chapter 11 deals with Hermite polynomials.
- Bayin, S.S. (2006) Mathematical Methods in Science and Engineering, Wiley, Chapter 4.
- Courant, Richard; Hilbert, David (), Methods of Mathematical Physics, Volume I, Wiley-Interscience.
- Fedoryuk, M.V. (), „Polinoame Hermite”, În Hazewinkel, Michiel, Encyclopaedia of Mathematics, Kluwer Academic Publishers, ISBN 978-1556080104.
- Wiener, Norbert (). The Fourier Integral and Certain of its Applications. New York: Dover Publications. ISBN 0-486-60272-9.
- Whittaker, E. T. (). A Course of Modern Analysis. London: Cambridge University Press. Parametru necunoscut
|ed=ignorat (ajutor)





































![{\displaystyle L[u]=u''-xu'=-\lambda u}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d1af1dbe9a17a96e69d0d602eca405acefc07f98)























![{\displaystyle H_{n}^{[\alpha ]}(x)\,\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4d1c07684d83d399feb259c6868adfe7a8b7557d)

![{\displaystyle H_{n}^{[\alpha ]}(x)=\alpha ^{-n/2}H_{n}^{[1]}\left({\frac {x}{\sqrt {\alpha }}}\right)=e^{-\alpha D^{2}/2}x^{n}.\,\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/71136220e40dea823690ea6f3b98d965ed26604a)
![{\displaystyle H_{n}^{[1/2]}(x).\,\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/77c6817045b48e630045144e6009f12377dd5687)
![{\displaystyle H_{n}^{[\alpha ]}(x)=\sum _{k=0}^{n}h_{n,k}^{[\alpha ]}x^{k}\,\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b96394b7718771b2e7f0ebe1569c6c0df8b25994)
![{\displaystyle \left(H_{n}^{[\alpha ]}\circ H^{[\beta ]}\right)(x)=\sum _{k=0}^{n}h_{n,k}^{[\alpha ]}\,H_{k}^{[\beta ]}(x)\,\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ba0bada37dc4e6abb2262f52f65168334c9d5da1)
![{\displaystyle \left(H_{n}^{[\alpha ]}\circ H^{[\beta ]}\right)(x)=H_{n}^{[\alpha +\beta ]}(x)\,\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/44bee65329f592b738e8119612c2237d217ca247)
![{\displaystyle H_{n}^{[\alpha +\beta ]}(x+y)=\sum _{k=0}^{n}{n \choose k}H_{k}^{[\alpha ]}(x)H_{n-k}^{[\beta ]}(y).\,\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8e6797d87f8ee008c710fd93ee0ae89ad250e844)
![{\displaystyle H_{n}^{[-\alpha ]}(x)\,\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2f89865d26dcf919504d573a15523a91430b65c1)
![{\displaystyle E(X^{n})=H_{n}^{[-\sigma ^{2}]}(\mu )\,\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8e307ed2f21e120cd382ced37071b455682bc311)
![{\displaystyle \sum _{k=0}^{n}{n \choose k}H_{k}^{[\alpha ]}(x)H_{n-k}^{[-\alpha ]}(y)=H_{n}^{[0]}(x+y)=(x+y)^{n}.\,\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8f0683c9b9b84456c42764b0a22fd2e21dec6cec)



















