Legea lui Amdahl
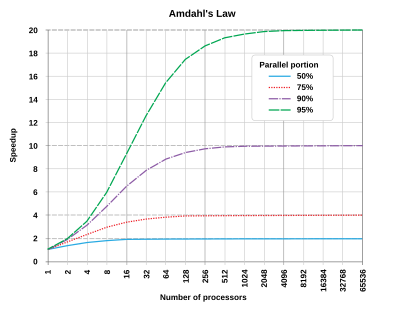
Legea lui Amdahl a fost enunțată de Gene Amdahl, inginer american, cunoscut datorită muncii sale în cadrul IBM. Acesta a definit limitările fundamentale ale programării paralele, propunând o evaluare a perfomanțelor mașinilor de calcul, în special în cazul utilizării de procesoare multiple. A fost prezentată la Conferința AFIPS din 1967.
Definiție[modificare | modificare sursă]
Se definește un factor de accelerare, , prin care se poate stabili de câte ori mașina îmbunătățită va rula mai repede. Acesta se calculează ca fiind raportul dintre timpul de execuție a unui task fără îmbunătățire și timpul de execuție folosind îmbunătățirea când e posibil. În unele cazuri această formulă este înlocuită de raportul dintre performanțele sistemului utilizând îmbunătățirea adusă și performanțele sistemului fără acea îmbunătățire
Din timpul total de rulare, orice îmbunătățire are o fracțiune de timp de utilizare.Pe baza definiției de mai sus se poate calcula un factor de accelerare doar pentru anumite îmbunătățiri:
unde este fracțiunea din timpul de calcul a mașinii inițiale care poate fi convertită pentru a putea profita de îmbunătățirea făcută, iar este îmbunătățirea - calculată ca raportul dintre noul timp de execuție (pentru porțiunea din task care beneficiază de îmbunătățirea făcută ) și timpul vechi de execuție Prin prelucrarea ecuației se obține
Corolar[modificare | modificare sursă]
Dacă îmbunătățirea este utilizată doar pentru o fracțiune din operație nu se poate accelera acea operație mai mult de 1/(1 – F)
Descriere[modificare | modificare sursă]
Legea lui Amdahl este un model prin care se creează o legătură între accelerarea dorită a paralelizării implementate a unui algoritm relativ la algoritmul serial. Se presupune că mărimea cazului care se rulează rămâne acceași când este paralelizată.
Spre exemplu, dacă pentru o problemă dată, o implementare paralelă a algoritmului de rezolvare poate rula 20% din timpul operațiilor (rămânâd ca 80% din algoritm sa fie neparalelizat), legea lui Amdahl spune că accelerarea maximă a versiunii paralelizate este de , adică versiunea paralelizată este de 1,25 ori mai rapidă decât versiunea ne-paralelizată.
Relația cu legea retururilor diminuate[modificare | modificare sursă]
Legea lui Amdahl este de foarte multe ori asociată cu legea retururilor diminuate, dar numai un caz special al aplicării legii lui Amdahl o demonstrează. Dacă se alege componenta optimală pentru îmbunătățire(în termeni de accelerare obținută), atunci se va observa că în timp ce această componentă va fi îmbunătățită, altor componente le va scădea îmbunătățirea proporțional. Dacă însă se vor alege componente neoptimale pentru îmbunătățire, se pot observa creșteri de îmbunătățire. Astfel, este de multe ori practic ca un sistem să fie îmbunătățit într-o ordine neoptimală, mai ales datorită faptului că unele îmbunătățiri sunt mai grele sau consumatoare de timp și resurse decât altele.
Legea retururilor diminuate se regăsește în cazul legii lui Amdahl dacă se ia în considerare tipul rezultatului în cazul adaugării unui procesor la mașină; dacă se rulează un sistem care va folosi toate procesoarele la capacitățile maxime. Fiecare nou procesor adăugat în sistem va adăuga mai puțină putere decât cel dinainte. De fiecare dată când se dublează numarul de procesoare, rația de accelerare a sistemului va scădea, rezultatul tinzând către o limită de Analiza nu ia în calcul apariția potențialelor gâtuiri(restricții) ale sistemului, cum ar fi banda de frecvență a memoriei sau a I/O; adar dacă acestea ar fi luate în calcul, adăugarea de procesoare pentru paralelizare ar avea și mai multe diminuări.
Vezi și[modificare | modificare sursă]
Bibliografie[modificare | modificare sursă]
- Validity of the Single Processor Approach to Achieving Large-Scale Computing Capabilities
- Amdahl’s Law Tutorial Arhivat în , la Wayback Machine.
Legături externe[modificare | modificare sursă]
- Simulare interactivă de cazuri
- Reevaluating Amdahl's law in the multicore era
- Modeling Critical Sections in Amdahl’s Law and its Implications for Multicore Design Arhivat în , la Wayback Machine.
| |||||








