Formula barometrică

Variaţia cu altitudinea a presiunii atmosferice

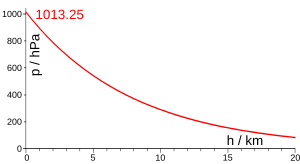
În mecanica fluidelor, formula barometrică este o formulă care stabilește dependența dintre presiunea atmosferică și altitudine.

Când în interiorul unui gaz nu există un gradient de temperatură, iar asupra sa nu acționează forțe exterioare, el are aceeași densitate în întreg volumul pe care îl ocupă; dacă asupra gazului acționează forțe gravitaționale, densitatea sa nu mai rămâne constantă. Astfel, densitatea ρ a aerului atmosferic variază cu altitudinea și, în ipoteza că temperatura T și accelerația gravitațională g nu variază cu înălțimea h, este dată de relația:

$\rho =\rho _{0}e^{-{\frac {mgh}{kT}}},$

unde:

• ρ₀ = densitatea la nivelul mării;
• m = masa medie a unei molecule de aer;
• k = constanta lui Boltzmann.

Deoarece:

$\rho =mn$

(unde n este concentrația moleculelor), rezultă:

$n=n_{0}e^{-{\frac {mgh}{kT}}}.$

Dar:

$n={\frac {p}{kT}}\;$   și  $\;n_{0}={\frac {p_{0}}{kT}}$

și se obține formula barometrică:

$p=p_{0}e^{-{\frac {mgh}{kT}}}.$

Această relație indică faptul că presiunea scade în progresie geometrică, atunci când altitudinea crește în progresie aritmetică și este aplicabilă doar pentru altitudini relativ mici (de ordinul miilor de metri). În cazul altitudinilor mari, relației i se aduc corecții legate de variațiile de temperaturii și accelerației gravitaționale cu altitudinea.