Factor de compresibilitate
Factorul de compresibilitate (Z), este un coeficient adimensional folosit la modificarea ecuației termice de stare a gazului ideal pentru a corespunde comportării unui gaz real. În acest sens, factorul de compresibilitate poate fi interpretat ca fiind o proprietate fizică a gazelor, valoarea sa depinzând de presiune, temperatură și natura gazului.[1]
În general, abaterea unui gaz față de comportarea gazului ideal devine semnificativă în vecinătatea curbei de saturație (la schimbarea de fază), sau la temperaturi scăzute, sau la presiuni ridicate. Valorile factorului de compresibilitate se calculează din ecuațiile de stare scrise de obicei în formă virială, în care constantele sunt determinate empiric. Valorile lui pentru un anumit gaz mai pot fi extrase dintr-o diagramă universală care reprezintă Z în funcție de presiunea redusă, având ca parametru temperatura redusă.[2][3]
Definire și semnificație fizică[modificare | modificare sursă]
Factorul de compresibilitate este definit drept:[2][4]
unde, este presiunea, este volumul molar al gazului, este temperatura absolută, și este constanta universală a gazelor.
Se poate exprima echivalent prin inlocuirea volumului molar cu cel masic respectiv inversul acestuia densitatea:
unde e densitatea gazului si e constanta specifică a gazelor adică raportul dintre constanta gazului ideal și masa molară a gazului.
Pentru un gaz ideal factorul de compresibilitate este prin definiție.[4] În multe din aplicații este necesar să fie luate în considerație abaterile gazului ideal față de gazul real. În general valoarea lui crește cu presiunea și scade cu temperatura. La presiune înaltă moleculele se ciocnesc mai des, iar la temperatură scăzută ele se mișcă mai încet. Asta face ca efectul forțelor intermoleculare să fie sesizabil, făcând ca volumul real al gazului () să fie mai mic decât cel al gazului ideal (), ceea ce determină ca să scadă sub unu.[5] Când presiunea este mai mică și temperatura mai mare moleculele au mai mult spațiu de mișcare. În acest caz se manifestă forțe de respingere, făcând ca . Cu cât gazul este într-o stare mai apropiată de punctul critic sau de saturație, cu atât abaterea de la cazul ideal crește (v. diagramele de mai jos).
Exemplu de valori experimentale[modificare | modificare sursă]
Este dificil de a stabili în general la ce presiuni și temperaturi abaterea de la gazul ideal devine importantă. În principiu, modelul gazului ideal este suficient de precis până la presiuni de 2 bar și chiar mai mari (până la 50 bar[6]) pentru molecule mici, neasociate. De exemplu, clorura de metil (CH3Cl, clormetan), care are o moleculă polară, având ca urmare forțe intermoleculare semnificative, are la presiunea de 10 atm și temperatura de 100 °C un factor de compresibilitate determinat experimental de Z = 0,9152.[7]. Pentru aer, care are molecule mici, nepolare, în condiții asemănătoare factorul de compresibilitate este Z = 1,0025 (v. tabelul de mai jos).
Compresibilitatea aerului[modificare | modificare sursă]
Compoziția chimică aproximativă a aerului este de 78 % azot, 21 % oxigen și 1 % alte gaze. Moleculele principalelor componente, azotul și oxigenul, sunt mici, nepolare (prin urmare neasociate). Ca urmare așteptările sunt ca aerul să se comporte aproape ca un gaz perfect, lucru confirmat de cercetările experimentale.
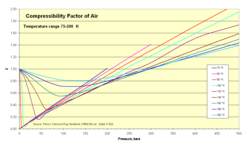
- 'Z pentru aer în funcție de presiune: 1 - 500 bar
-
Izoterme pentru 75 - 200 K
-
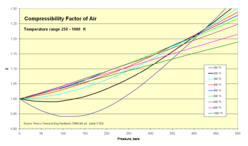
Izoterme pentru 250 - 1000 K
Valorile Z din tabelul următor au fost calculate în funcție de presiune, temperatură și volum (sau densitate) din lucrările lui Vassernan, Kazavcinski și Rabinovici.[8][9]
| Presiune absolută (bar) | ||||||||||||||
| Temp. (K) | 1 | 5 | 10 | 20 | 40 | 60 | 80 | 100 | 150 | 200 | 250 | 300 | 400 | 500 |
| 75 | 0,0052 | 0,0260 | 0,0519 | 0,1036 | 0,2063 | 0,3082 | 0,4094 | 0,5099 | 0,7581 | 1,0125 | ||||
| 80 | 0,0250 | 0,0499 | 0,0995 | 0,1981 | 0,2958 | 0,3927 | 0,4887 | 0,7258 | 0,9588 | 1,1931 | 1,4139 | |||
| 90 | 0,9764 | 0,0236 | 0,0453 | 0,0940 | 0,1866 | 0,2781 | 0,3686 | 0,4681 | 0,6779 | 0,8929 | 1,1098 | 1,3110 | 1,7161 | 2,1105 |
| 100 | 0,9797 | 0,8872 | 0,0453 | 0,0900 | 0,1782 | 0,2635 | 0,3498 | 0,4337 | 0,6386 | 0,8377 | 1,0395 | 1,2227 | 1,5937 | 1,9536 |
| 120 | 0,9880 | 0,9373 | 0,8860 | 0,6730 | 0,1778 | 0,2557 | 0,3371 | 0,4132 | 0,5964 | 0,7720 | 0,9530 | 1,1076 | 1,5091 | 1,7366 |
| 140 | 0,9927 | 0,9614 | 0,9205 | 0,8297 | 0,5856 | 0,3313 | 0,3737 | 0,4340 | 0,5909 | 0,7699 | 0,9114 | 1,0393 | 1,3202 | 1,5903 |
| 160 | 0,9951 | 0,9748 | 0,9489 | 0,8954 | 0,7803 | 0,6603 | 0,5696 | 0,5489 | 0,6340 | 0,7564 | 0,8840 | 1,0105 | 1,2585 | 1,4970 |
| 180 | 0,9967 | 0,9832 | 0,9660 | 0,9314 | 0,8625 | 0,7977 | 0,7432 | 0,7084 | 0,7180 | 0,7986 | 0,9000 | 1,0068 | 1,2232 | 1,4361 |
| 200 | 0,9978 | 0,9886 | 0,9767 | 0,9539 | 0,9100 | 0,8701 | 0,8374 | 0,8142 | 0,8061 | 0,8549 | 0,9311 | 1,0185 | 1,2054 | 1,3944 |
| 250 | 0,9992 | 0,9957 | 0,9911 | 0,9822 | 0,9671 | 0,9549 | 0,9463 | 0,9411 | 0,9450 | 0,9713 | 1,0152 | 1,0702 | 1,1990 | 1,3392 |
| 300 | 0,9999 | 0,9987 | 0,9974 | 0,9950 | 0,9917 | 0,9901 | 0,9903 | 0,9930 | 1,0074 | 1,0326 | 1,0669 | 1,1089 | 1,2073 | 1,3163 |
| 350 | 1,0000 | 1,0002 | 1,0004 | 1,0014 | 1,0038 | 1,0075 | 1,0121 | 1,0183 | 1,0377 | 1,0635 | 1,0947 | 1,1303 | 1,2116 | 1,3015 |
| 400 | 1,0002 | 1,0012 | 1,0025 | 1,0046 | 1,0100 | 1,0159 | 1,0229 | 1,0312 | 1,0533 | 1,0795 | 1,1087 | 1,1411 | 1,2117 | 1,2890 |
| 450 | 1,0003 | 1,0016 | 1,0034 | 1,0063 | 1,0133 | 1,0210 | 1,0287 | 1,0374 | 1,0614 | 1,0913 | 1,1183 | 1,1463 | 1,2090 | 1,2778 |
| 500 | 1,0003 | 1,0020 | 1,0034 | 1,0074 | 1,0151 | 1,0234 | 1,0323 | 1,0410 | 1,0650 | 1,0913 | 1,1183 | 1,1463 | 1,2051 | 1,2667 |
| 600 | 1,0004 | 1,0022 | 1,0039 | 1,0081 | 1,0164 | 1,0253 | 1,0340 | 1,0434 | 1,0678 | 1,0920 | 1,1172 | 1,1427 | 1,1947 | 1,2475 |
| 800 | 1,0004 | 1,0020 | 1,0038 | 1,0077 | 1,0157 | 1,0240 | 1,0321 | 1,0408 | 1,0621 | 1,0844 | 1,1061 | 1,1283 | 1,1720 | 1,2150 |
| 1000 | 1,0004 | 1,0018 | 1,0037 | 1,0068 | 1,0142 | 1,0215 | 1,0290 | 1,0365 | 1,0556 | 1,0744 | 1,0948 | 1,1131 | 1,1515 | 1,1889 |
Compresibilitatea amoniacului[modificare | modificare sursă]
Amoniacul (NH3) are molecule mici, polare, cu forțe intermoleculare semnificative. Valorile Z se pot obține din manualul lui Perry, ed. a 4-a.
Diagrama universală a factorului de compresibilitate pentru gaze pure[modificare | modificare sursă]
Relația universală între factorul de compresibilitate și presiunea redusă , respectiv temperatura redusă a fost constatată pentru prima oară de Van der Waals în 1873 și este cunoscută ca legea stărilor corespondente. Această lege exprimă constatarea că proprietățile unui gaz care depind de forțele intermoleculare sunt legate de proprietățile gazului în punctul critic. Asta oferă o bază pentru corelarea proprietăților moleculare. Legea afirmă că orice gaz pur la aceeași presiune și temperatură redusă are același factor de compresibilitate. Presiunea și temperatura redusă sunt definite drept:
- , respectiv
unde și sunt presiunea și temperatura critică a gazului. Acestea sunt specifice fiecărui gaz, temperatura critică fiind aceea peste care este imposibilă lichefierea gazului, iar presiunea critică este presiunea maximă la care lichefierea este posibilă (la temperatura critică). Împreună ele definesc punctul critic, deasupra căruia existența simultană a fazelor lichidă și gazoasă nu este posibilă.

Valorile factorului de compresibilitate a gazelor reale în funcție de parametrii p, T și V diferă de la un gaz la altul, însă alura izotermelor într-o diagramă este asemănătoare. Pe baza comparării valorilor experimentale exprimate în funcție de presiunile și temperaturile reduse se pot construi diagrame „universale” ale factorului de compresibilitate. În figura alăturată este prezentată o asemenea diagramă, construită pe baza a 10 gaze (majoritatea alcani): metan, etan, etenă, propan, n-butan, i-pentan, n-hexan, azot, dioxid de carbon, și vapori de apă, diagramă uzuală la determinarea factorului de compresibilitate la livrările de gaz natural.
Alte diagrame universale se poate găsi în bibliografia de specialitate.[2][11]
Se pot construi și alte diagrame detaliate, cum sunt diagramele Nelson-Obert, construite pe baza a 25 gaze pure. Se afirmă că precizia acestor diagrame este de 1-2 % pentru Z > 0,6 și de 4-6 % pentru Z cuprins între 0,3 – 0,6. Alte lucrări menționează erori asemănătoare, de 3-5 %.[2]
Diagramele universale pot avea erori mari (până la 15 – 20 %) la gaze cu molecule puternic polare, în care centrele sarcinilor pozitive și negative nu coincid.
Hidrogenul, heliul și neonul nu se conformează legii stărilor corespondente. Pentru a putea folosi și pentru ele diagramele universale, pentru aceste gaze se folosesc în acest caz presiuni și temperaturi reduse convenționale:
- , respectiv
Modele teoretice[modificare | modificare sursă]
Forma virială a ecuației este utilă pentru descrierea cauzelor abaterii de la gazul ideal la nivel molecular (foarte puține gaze sunt monoatomice) și este obținută direct din mecanica statistică:
unde coeficienții de la numărător se numesc coeficienți viriali și sunt funcții de temperatură.
Coeficienții viriali indică interacțiunile între diversele grupuri de molecule. Coeficientul indică interacțiunile între perechile de molecule, între grupuri de trei molecule etc. Deoarece interacțiunile între un număr mai mare de molecule sunt rare, ecuația virială este de obicei trunchiată după al treilea termen.[12]
Factorul de compresibilitate este legat de potențialul al forțelor intermoleculare prin relația:
fiind distanța dintre molecule.[13]
Alte modele teoretice care permit calcularea factorului de compresibilitate urmează a fi expuse în articolul gaz real.
Fugacitate[modificare | modificare sursă]
Factorul de compresibilitate este legat de coeficientul de fugacitate prin formula:
Aplicații[modificare | modificare sursă]
Una dintre principalele aplicații este determinarea exactă a cantităților de gaz natural livrate, unde este obligatoriu să fie luat în considerare factorul de compresibilitate.[16] Metodele oficiale de calcul ale factorului de compresibilitate al gazului natural pe baza ecuației viriale trunchiate sunt standardizate.[17][18]
Note[modificare | modificare sursă]
- ^ SR ISO 15970:2010 Gaz natural. Măsurarea proprietăților. Proprietăți volumetrice: densitate, presiune, temperatură și factor de compresibilitate.
- ^ a b c d Bazil Popa ș.a. Manualul inginerului termotehnician, vol I, București: Editura Tehnică, 1984, p. 182
- ^ en M. Parlaktuna, J.-S. Gudmundsson -Physical Properties of Natural Gases: Computer Programme And Subroutines Arhivat în , la Wayback Machine., Technical Report, 1991, Chap. 3, accesat 2010-07-09
- ^ a b Ioan Vlădea Tratat de termodinamică tehnică și transmiterea căldurii, București: Editura Didactică și Pedagogică, 1974, p. 114
- ^ en Donald A McQuarrie, John D. Simon - Molecular Thermodynamics, University Science Books, 1999, ISBN 1-891389-05-X, p. 55
- ^ George C. Moisil - Termodinamica, București: Editura Academiei RSR, 1988, p. 229
- ^ Perry, pp.3-268
- ^ en Vassernan, Kazavchinskii, Rabinovich - Thermophysical Properties of Air and Air Components, Moscova: Nauka, 1966, și NBS-NSF Trans. TT 70-50095, 1971
- ^ en Vassernan, Rabinovich - "Thermophysical Properties of Liquid Air and Its Component, Moscova: Nauka, 1968, și NBS-NSF Trans. 69-55092, 1970.
- ^ Perry, tab. 3-162
- ^ ru Teplotehniceskii spravocinik, vol I și II, ed. a 2-a, Moscova: Ed. Eherghia, 1975-1976
- ^ en J. M. Smith - Introduction to Chemical Engineering Thermodynamics, ed. a 7-a, McGraw Hill, 2005, ISBN 0-07-310445-0, p. 73
- ^ Gabriela Lisa, Chimie fizică 1. Termodinamică, Editura Performantica, Iași 2008, p 20
- ^ Redlich, Otto; Kwong, J. N. S. (). „On The Thermodynamics of Solutions”. Chem. Rev. 44 (1): 233–244. doi:10.1021/cr60137a013. PMID 18125401.
- ^ Murgulescu p360
- ^ Normă de metrologie legală NML 018-06 Sisteme de măsurare continuă și dinamică a cantităților de fluide (de volum și de masă) Arhivat în , la Wayback Machine., brml.ro, accesat 2010-07-13
- ^ en AGA Report No. 8, Compressibility Factor of Natural Gas and Related Hydrocarbon Gases (1994)
- ^ en ISO12213-3:1997 Natural gas. Calculation of compression factors. Calculation using measured physical properties.
Bibliografie[modificare | modificare sursă]
- en Perry's chemical engineers' handbook, ed. a 6-a, MCGraw-Hill, 1984, ISBN 0-07-049479-7
- ro Dan Geană, Viorel Feroiu București: Ecuații de stare - Aplicații la echilibre de faze, Editura Tehnică, București, 2000
- ro Bazil Popa ș.a. Manualul inginerului termotehnician, vol I, București: Editura Tehnică, 1984
- ro Moisil, George C. - Termodinamica, București: Editura Academiei RSR, 1988
- ro Murgulescu, I.G., Segal, E.- Introducere în chimia fizică, vol. II, 1-Teoria molecular-cinetică a materiei, București: Editura Academiei RSR, 1979
- ro Ioan Vlădea Tratat de termodinamică tehnică și transmiterea căldurii, București: Editura Didactică și Pedagogică, 1974
Vezi și[modificare | modificare sursă]
Legături externe[modificare | modificare sursă]
- en Real Gases Arhivat în , la Wayback Machine., unde se prezintă și factorul de compresibilitate.
- „Programul Z” pentru determinarea factorului de abatere Z pentru ecuația de stare a gazelor reale îm Revista Termotehnica